湖北省荆州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类(含答案)

这是一份湖北省荆州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类(含答案)，共31页。试卷主要包含了x+b，已知等内容，欢迎下载使用。

湖北省荆州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
一．分式的化简求值（共1小题）
1．（2023•荆州）先化简，再求值：（﹣）÷，其中x＝（）﹣1，y＝（﹣2023）0．
二．解一元二次方程-配方法（共1小题）
2．（2021•荆州）已知：a是不等式5（a﹣2）+8＜6（a﹣1）+7的最小整数解，请用配方法解关于x的方程x2+2ax+a+1＝0．
三．分式方程的应用（共1小题）
3．（2023•荆州）荆州古城旁“荆街”某商铺打算购进A，B两种文创饰品对游客销售．已知1400元采购A种的件数是630元采购B种件数的2倍，A种的进价比B种的进价每件多1元，两种饰品的售价均为每件15元；计划采购这两种饰品共600件，采购B种的件数不低于390件，不超过A种件数的4倍．
（1）求A，B饰品每件的进价分别为多少元？
（2）若采购这两种饰品只有一种情况可优惠，即一次性采购A种超过150件时，A种超过的部分按进价打6折．设购进A种饰品x件，
①求x的取值范围；
②设计能让这次采购的饰品获利最大的方案，并求出最大利润．
四．反比例函数综合题（共1小题）
4．（2022•荆州）小华同学学习函数知识后，对函数通过列表、描点、连线，画出了如图1所示的图象．
x
…
﹣4
﹣3
﹣2
﹣1
﹣
﹣
﹣
0
1
2
3
4
…
y
…
1

2
4

1

0
﹣4
﹣2
﹣
﹣1
…
请根据图象解答：
（1）【观察发现】
①写出函数的两条性质：　 　； 　 　；
②若函数图象上的两点（x1，y1），（x2，y2）满足x1+x2＝0，则y1+y2＝0一定成立吗？　 　．（填“一定”或“不一定”）
（2）【延伸探究】如图2，将过A（﹣1，4），B（4，﹣1）两点的直线向下平移n个单位长度后（n≥0），得到直线l与函数y＝﹣（x≤﹣1）的图象交于点P，连接PA，PB．
①求当n＝3时，直线l的解析式和△PAB的面积；
②直接用含n的代数式表示△PAB的面积．

五．二次函数综合题（共2小题）
5．（2023•荆州）已知：y关于x的函数y＝（a﹣2）x2+（a+1）x+b．
（1）若函数的图象与坐标轴有两个公共点，且a＝4b，则a的值是 　 　；
（2）如图，若函数的图象为抛物线，与x轴有两个公共点A（﹣2，0），B（4，0），并与动直线l：x＝m（0＜m＜4）交于点P，连接PA，PB，PC，BC，其中PA交y轴于点D，交BC于点E．设△PBE的面积为S1，△CDE的面积为S2．
①当点P为抛物线顶点时，求△PBC的面积；
②探究直线l在运动过程中，S1﹣S2是否存在最大值？若存在，求出这个最大值；若不存在，说明理由．

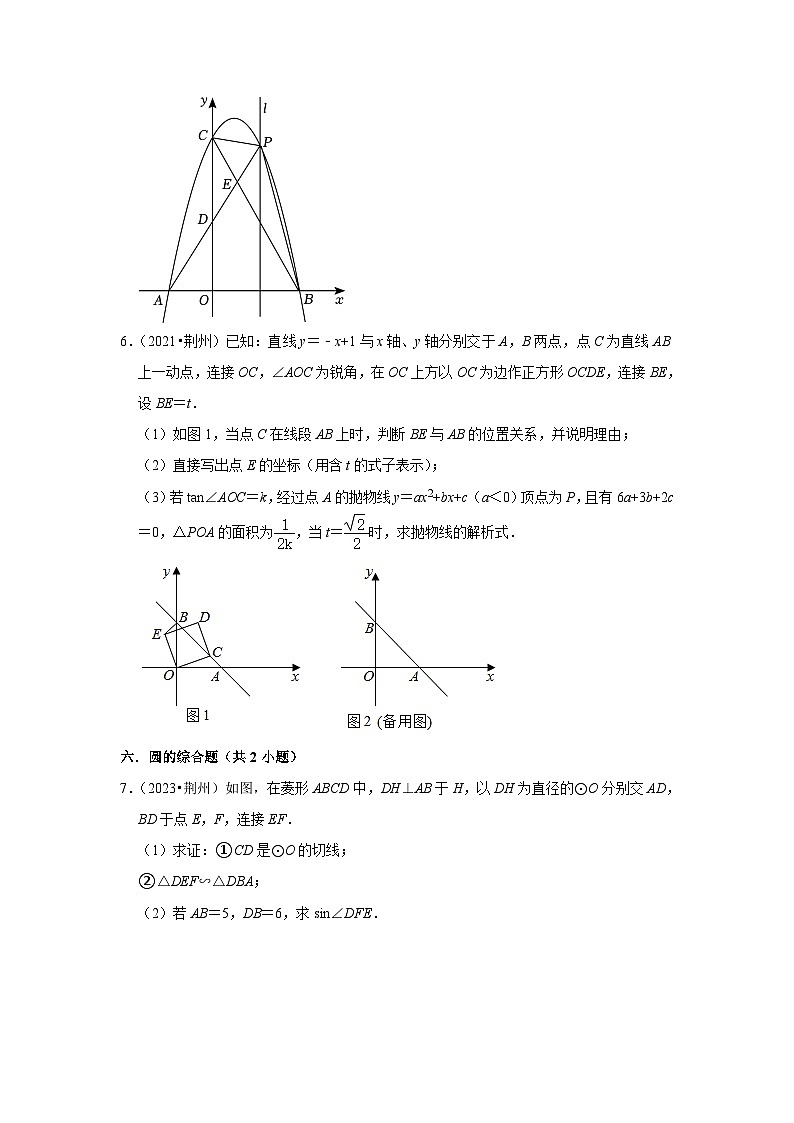
6．（2021•荆州）已知：直线y＝﹣x+1与x轴、y轴分别交于A，B两点，点C为直线AB上一动点，连接OC，∠AOC为锐角，在OC上方以OC为边作正方形OCDE，连接BE，设BE＝t．
（1）如图1，当点C在线段AB上时，判断BE与AB的位置关系，并说明理由；
（2）直接写出点E的坐标（用含t的式子表示）；
（3）若tan∠AOC＝k，经过点A的抛物线y＝ax2+bx+c（a＜0）顶点为P，且有6a+3b+2c＝0，△POA的面积为，当t＝时，求抛物线的解析式．

六．圆的综合题（共2小题）
7．（2023•荆州）如图，在菱形ABCD中，DH⊥AB于H，以DH为直径的⊙O分别交AD，BD于点E，F，连接EF．
（1）求证：①CD是⊙O的切线；
②△DEF∽△DBA；
（2）若AB＝5，DB＝6，求sin∠DFE．

8．（2022•荆州）如图1，在矩形ABCD中，AB＝4，AD＝3，点O是边AB上一个动点（不与点A重合），连接OD，将△OAD沿OD折叠，得到△OED；再以O为圆心，OA的长为半径作半圆，交射线AB于G，连接AE并延长交射线BC于F，连接EG，设OA＝x．
（1）求证：DE是半圆O的切线：
（2）当点E落在BD上时，求x的值；
（3）当点E落在BD下方时，设△AGE与△AFB面积的比值为y，确定y与x之间的函数关系式；
（4）直接写出：当半圆O与△BCD的边有两个交点时，x的取值范围．


七．作图—复杂作图（共1小题）
9．（2022•荆州）如图，在10×10的正方形网格中，小正方形的顶点称为格点，顶点均在格点上的图形称为格点图形，图中△ABC为格点三角形．请按要求作图，不需证明．
（1）在图1中，作出与△ABC全等的所有格点三角形，要求所作格点三角形与△ABC有一条公共边，且不与△ABC重叠；
（2）在图2中，作出以BC为对角线的所有格点菱形．


八．作图—应用与设计作图（共1小题）
10．（2021•荆州）如图，在5×5的正方形网格图形中，小正方形的边长都为1，线段ED与AD的端点都在网格小正方形的顶点（称为格点）上．
请在网格图形中画图：
（1）以线段AD为边画正方形ABCD，再以线段DE为斜边画等腰直角三角形DEF，其中顶点F在正方形ABCD外；
（2）在（1）中所画图形基础上，以点B为其中一个顶点画一个新正方形，使新正方形的面积为正方形ABCD和△DEF面积之和，其它顶点也在格点上．

九．几何变换综合题（共1小题）
11．（2023•荆州）如图1，点P是线段AB上与点A，点B不重合的任意一点，在AB的同侧分别以A，P，B为顶点作∠1＝∠2＝∠3，其中∠1与∠3的一边分别是射线AB和射线BA，∠2的两边不在直线AB上，我们规定这三个角互为等联角，点P为等联点，线段AB为等联线．
（1）如图2，在5×3个方格的纸上，小正方形的顶点为格点、边长均为1，AB为端点在格点的已知线段．请用三种不同连接格点的方法，作出以线段AB为等联线、某格点P为等联点的等联角，并标出等联角，保留作图痕迹；
（2）如图3，在Rt△APC中，∠A＝90°，AC＞AP，延长AP至点B，使AB＝AC，作∠A的等联角∠CPD和∠PBD．将△APC沿PC折叠，使点A落在点M处，得到△MPC，再延长PM交BD的延长线于E，连接CE并延长交PD的延长线于F，连接BF．
①确定△PCF的形状，并说明理由；
②若AP：PB＝1：2，BF＝k，求等联线AB和线段PE的长（用含k的式子表示）．

一十．相似形综合题（共1小题）
12．（2021•荆州）在矩形ABCD中，AB＝2，AD＝4，F是对角线AC上不与点A，C重合的一点，过F作FE⊥AD于E，将△AEF沿EF翻折得到△GEF，点G在射线AD上，连接CG．
（1）如图1，若点A的对称点G落在AD上，∠FGC＝90°，延长GF交AB于H，连接CH．
①求证：△CDG∽△GAH；
②求tan∠GHC．
（2）如图2，若点A的对称点G落在AD延长线上，∠GCF＝90°，判断△GCF与△AEF是否全等，并说明理由．

一十一．解直角三角形的应用-仰角俯角问题（共1小题）
13．（2022•荆州）荆州城徽“金凤腾飞”立于古城东门外．如图，某校学生测量其高AB（含底座），先在点C处用测角仪测得其顶端A的仰角为32°，再由点C向城徽走6.6m到E处，测得顶端A的仰角为45°．已知B，E，C三点在同一直线上，测角仪离地面的高度CD＝EF＝1.5m，求城徽的高AB．（参考数据：sin32°≈0.530，cos32°≈0.848，tan32°≈0.625）．

一十二．列表法与树状图法（共1小题）
14．（2022•荆州）为弘扬荆州传统文化，我市将举办中小学生“知荆州、爱荆州、兴荆州”知识竞赛活动．某校举办选拔赛后，随机抽取了部分学生的成绩，按成绩（百分制）分为A，B，C，D四个等级，并绘制了如下不完整的统计图表．
等级
成绩（x）
人数
A
90＜x≤100
m
B
80＜x≤90
24
C
70＜x≤80
14
D
x≤70
10
根据图表信息，回答下列问题：
（1）表中m＝　 　；扇形统计图中，B等级所占百分比是 　 　，C等级对应的扇形圆心角为 　 　度；
（2）若全校有1400人参加了此次选拔赛，则估计其中成绩为A等级的共有 　 　人；
（3）若全校成绩为100分的学生有甲、乙、丙、丁4人，学校将从这4人中随机选出2人参加市级竞赛．请通过列表或画树状图，求甲、乙两人至少有1人被选中的概率．


湖北省荆州市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
参考答案与试题解析
一．分式的化简求值（共1小题）
1．（2023•荆州）先化简，再求值：（﹣）÷，其中x＝（）﹣1，y＝（﹣2023）0．
【答案】，2．
【解答】解：原式＝[﹣]•
＝（﹣）•
＝•
＝，
∵x＝（）﹣1＝2，y＝（﹣2023）0＝1，
∴原式＝＝2．
二．解一元二次方程-配方法（共1小题）
2．（2021•荆州）已知：a是不等式5（a﹣2）+8＜6（a﹣1）+7的最小整数解，请用配方法解关于x的方程x2+2ax+a+1＝0．
【答案】x1＝2+，x2＝2﹣．
【解答】解：解不等式5（a﹣2）+8＜6（a﹣1）+7，得a＞﹣3，
∴最小整数解为﹣2，
将a＝﹣2代入方程x2+2ax+a+1＝0，得x2﹣4x﹣1＝0，
配方，得（x﹣2）2＝5．
直接开平方，得x﹣2＝±．
解得x1＝2+，x2＝2﹣．
三．分式方程的应用（共1小题）
3．（2023•荆州）荆州古城旁“荆街”某商铺打算购进A，B两种文创饰品对游客销售．已知1400元采购A种的件数是630元采购B种件数的2倍，A种的进价比B种的进价每件多1元，两种饰品的售价均为每件15元；计划采购这两种饰品共600件，采购B种的件数不低于390件，不超过A种件数的4倍．
（1）求A，B饰品每件的进价分别为多少元？
（2）若采购这两种饰品只有一种情况可优惠，即一次性采购A种超过150件时，A种超过的部分按进价打6折．设购进A种饰品x件，
①求x的取值范围；
②设计能让这次采购的饰品获利最大的方案，并求出最大利润．
【答案】（1）A种饰品每件的进价为10元，则B种饰品每件的进价为9元；
（2）①120≤x≤210，且x为整数；
②当采购A种饰品210件，B种饰品390件，商铺获利最大，最大利润为3630元．
【解答】解：（1）设A种饰品每件的进价为a元，则B种饰品每件的进价为（a﹣1）元，
由题意得：＝×2，
解得：a＝10，
经检验，a＝10是所列方程的解，且符合题意，
a﹣1＝9，
答：A种饰品每件的进价为10元，则B种饰品每件的进价为9元；
（2）①由题意得：，
解得：120≤x≤210，
∴购进A种饰品件数x的取值范围为：120≤x≤210，且x为整数；
②设采购A种饰品x件时的总利润为w元，
当120≤x≤150时，w＝15×600﹣10x﹣9（600﹣x）＝﹣x+3600，
∵﹣1＜0，
∴w随x的增大而减小，
∴当x＝120时，w有最大值是：﹣120+3600＝3480，
当150＜x≤210时，w＝15×600﹣[10×150+10×60%（x﹣150）]﹣9（600﹣x）＝3x+3000，
∵3＞0，
∴w随x的增大而增大，
∴当x＝210时，w有最大值是：3×210+3000＝3630，
∵3630＞3480，
∴w的最大值是3630，此时600﹣x＝600﹣210＝390，
即当采购A种饰品210件，B种饰品390件，商铺获利最大，最大利润为3630元．
四．反比例函数综合题（共1小题）
4．（2022•荆州）小华同学学习函数知识后，对函数通过列表、描点、连线，画出了如图1所示的图象．
x
…
﹣4
﹣3
﹣2
﹣1
﹣
﹣
﹣
0
1
2
3
4
…
y
…
1

2
4

1

0
﹣4
﹣2
﹣
﹣1
…
请根据图象解答：
（1）【观察发现】
①写出函数的两条性质：　函数有最大值为4　； 　当x＞0时，y随x的增大而增大　；
②若函数图象上的两点（x1，y1），（x2，y2）满足x1+x2＝0，则y1+y2＝0一定成立吗？　不一定　．（填“一定”或“不一定”）
（2）【延伸探究】如图2，将过A（﹣1，4），B（4，﹣1）两点的直线向下平移n个单位长度后（n≥0），得到直线l与函数y＝﹣（x≤﹣1）的图象交于点P，连接PA，PB．
①求当n＝3时，直线l的解析式和△PAB的面积；
②直接用含n的代数式表示△PAB的面积．

【答案】（1）①函数有最大值为4，当x＞0时，y随x的增大而增大（答案不唯一）；
②不一定；
（2）①直线l的解析式为y＝﹣x，△PAB的面积为；
②△PAB的面积为．
【解答】解：（1）①由图象知：函数有最大值为4，当x＞0时，y随x的增大而增大（答案不唯一）；
故答案为：函数有最大值为4，当x＞0时，y随x的增大而增大（答案不唯一）；
②假设x1＝﹣，则y1＝1，
∵x1+x2＝0，
∴x2＝，
∴y2＝﹣8，
∴y1+y2＝0不一定成立，
故答案为：不一定；
（2）①设直线AB的解析式为y＝kx+b，
则，
解得，
∴直线AB的解析式为y＝﹣x+3，
当n＝3时，直线l的解析式为y＝﹣x+3﹣3＝﹣x，
设直线AB与y轴交于C，

则△PAB的面积＝△AOB的面积，
∴S△AOB＝S△AOC+S△BOC＝＝＝，
∴△PAB的面积为；
②设直线l与y轴交于D，
∵l∥AB，
∴△PAB的面积＝△ABD的面积，

由题意知，CD＝n，
∴S△ABD＝S△ACD+S△BCD
＝
＝．
∴△PAB的面积为．
五．二次函数综合题（共2小题）
5．（2023•荆州）已知：y关于x的函数y＝（a﹣2）x2+（a+1）x+b．
（1）若函数的图象与坐标轴有两个公共点，且a＝4b，则a的值是 　0或2或﹣　；
（2）如图，若函数的图象为抛物线，与x轴有两个公共点A（﹣2，0），B（4，0），并与动直线l：x＝m（0＜m＜4）交于点P，连接PA，PB，PC，BC，其中PA交y轴于点D，交BC于点E．设△PBE的面积为S1，△CDE的面积为S2．
①当点P为抛物线顶点时，求△PBC的面积；
②探究直线l在运动过程中，S1﹣S2是否存在最大值？若存在，求出这个最大值；若不存在，说明理由．

【答案】（1）2或0或﹣；
（2）①6；
②当m＝时，S1﹣S2存在最大值，最大值为．
【解答】解：（1）①当a﹣2＝0时，即a＝2时，
y关于x的函数解析式为y＝3x+，
此时y＝3x+与x轴的交点坐标为（﹣，0），
与y轴的交点坐标为（0，）；
②当a﹣2≠0时，y关于x的函数为二次函数，
∵二次函数图象抛物线与坐标轴有两个交点，
∴抛物线可能存在与x轴有两个交点，其中一个交点为坐标原点或与x轴有一个交点与y轴一个交点两种情况．
当抛物线与x轴有两个交点且一个为坐标原点时，
由题意得b＝0，此时a＝0，抛物线为y＝﹣2x2+x．
当y＝0时，﹣2x2+x＝0，
解得x1＝0，x2＝．
∴其图象与x轴的交点坐标为（0，0）（，0）．
当抛物线与x轴有一个交点与y轴有一个交点时，
由题意得，y＝（a﹣2）x2+（a+1）x+b所对应的一元二次方程（a﹣2）x2+（a+1）x+b＝0有两个相等实数根．
∴Δ＝（a+1）2﹣4（a﹣2）×a＝0，
解得a＝﹣，
此时y＝﹣x2+x﹣，
当x＝0时，y＝﹣，
∴与y轴的交点坐标为（0，﹣），
当y＝0时，﹣x2+x﹣＝0，
解得x1＝x2＝，
∴与x轴的交点坐标为（，0），
综上所述，若y关于x的函数y＝（a﹣2）x2+（a+1）x+b的图象与坐标轴有两个交点，则a可取的值为2，0，﹣，
故答案为：2或0或﹣；
（2）①如图，设直线l与BC交于点F，
根据题意得，
解得，
∴抛物线的解析式为y＝﹣x2+2x+8，
当x＝0时，y＝8，
∴C（0，8），
∵y＝﹣x2+2x+8＝﹣（x﹣1）2+9，点P为抛物线顶点，
∴P（1，9），
∵B（4，0），C（0，8），
∴直线BC的解析式为y＝﹣2x+8，
∴F（1，6），
∴PF＝9﹣6＝3，
∴△PBC的面积＝OB•PF＝＝6；
②S1﹣S2存在最大值，
理由：如图，设直线x＝m交x轴于H，
由①得，OB＝4，AO＝2，AB＝6，OC＝8，AH＝2+m，P（m，﹣m2+2m+8），
∴PH＝﹣m2+2m+8，
∵OD∥PH，
∴△AOD∽△AHP，
∴，
∴，
∴OD＝8﹣2m，
∵S1﹣S2＝S△PAB﹣S△AOD﹣S△OBC＝＝﹣3m2+8m＝﹣3（m﹣）2+，
∵﹣3＜0，0＜m＜4，
∴当m＝时，S1﹣S2存在最大值，最大值为．

6．（2021•荆州）已知：直线y＝﹣x+1与x轴、y轴分别交于A，B两点，点C为直线AB上一动点，连接OC，∠AOC为锐角，在OC上方以OC为边作正方形OCDE，连接BE，设BE＝t．
（1）如图1，当点C在线段AB上时，判断BE与AB的位置关系，并说明理由；
（2）直接写出点E的坐标（用含t的式子表示）；
（3）若tan∠AOC＝k，经过点A的抛物线y＝ax2+bx+c（a＜0）顶点为P，且有6a+3b+2c＝0，△POA的面积为，当t＝时，求抛物线的解析式．

【答案】（1）见解答；（2）（﹣t，1﹣t）或（t，1+t）；（3）y＝﹣3x2+12x﹣9或y＝﹣x2+4x﹣3．
【解答】解：（1）直线y＝﹣x+1与x轴、y轴分别交于A，B两点，
则点A、B的坐标分别为（1，0）、（0，1），
则∠OBA＝∠OAB＝45°，
∵∠AOC+∠BOC＝90°，∠BOC+∠BOE＝90°，
∴∠AOC＝∠BOE，
∵AO＝BO，OC＝OE，
∴△OAC≌△OBE（SAS），
∴∠OBE＝∠OAC＝45°，AC＝BE＝t，
∴∠EBA＝∠EBO+∠OBA＝∠OAC+∠OBA＝45°+45°＝90°，
∴BE⊥AB；

（2）①当点C在线段AB上时，如图1﹣1，
过点E作EH⊥OB于点H，

∵∠EBH＝45°，
∴BH＝EH＝BE＝t，
故点E的坐标为（﹣t，1﹣t）；
②当点C在线段BA的延长线上时，如图1﹣2，

同理可得，点E的坐标为（t，1+t）；
综上，点E的坐标为（﹣t，1﹣t）或（t，1+t）；

（3）①当点C线段AB上时，如题图1﹣1，
过点C作CN⊥OA于点N，
当t＝时，即AC＝t＝，
则CN＝AN＝t＝，
则ON＝OA﹣NA＝1﹣＝CN，
故tan∠AOC＝＝1＝k，
∵△POA的面积＝×AO×yP＝×1×yP＝＝，
解得yP＝1＝c﹣①，
∵抛物线过点A（1，0），故a+b+c＝0②，
而6a+3b+2c＝0③，
联立①②③并解得，
∴抛物线的表达式为y＝﹣x2+4x﹣3；
②抛物线过点A，则a+b+c＝0，
而6a+3b+2c＝0，
联立上述两式并解得：，
故抛物线的表达式为y＝a（x﹣2）2﹣a（a＜0），
则点P的坐标为（2，﹣a），

则AC＝BE＝t＝，
则tan∠AOC＝k＝＝，
故a＝﹣3，
故y＝﹣3x2+12x﹣9．
综上，y＝﹣3x2+12x﹣9或y＝﹣x2+4x﹣3．
六．圆的综合题（共2小题）
7．（2023•荆州）如图，在菱形ABCD中，DH⊥AB于H，以DH为直径的⊙O分别交AD，BD于点E，F，连接EF．
（1）求证：①CD是⊙O的切线；
②△DEF∽△DBA；
（2）若AB＝5，DB＝6，求sin∠DFE．

【答案】（1）①②证明见解答过程；
（2）sin∠DFE＝．
【解答】（1）证明：①∵四边形ABCD是菱形，
∴AB∥CD，
∵DH⊥AB，
∴∠CDH＝∠DHA＝90°，
∴CD⊥OD，
∵D为⊙O的半径的外端点，
∴CD是⊙O的切线；
②连接HF，

∴∠DEF＝∠DHF，
∵DH为⊙O直径，
∴∠DFH＝90°，
∴∠DHF＝90°﹣∠BDH，
∵∠DHB＝90°，
∴∠DBA＝90°﹣∠BDH，
∴∠DHF＝∠DBA＝∠DEF，
∵∠EDF＝∠BDA，
∴△DEF∽△DBA；
（2）解：连接AC交BD于G．

∵菱形ABCD，BD＝6，
∴AC⊥BD，AG＝GC，DG＝GB＝3，
在Rt△AGB中，AG＝＝4，
∴AC＝2AG＝8，
∵S菱形ABCD＝AC•BD＝AB•DH，
∴DH＝＝，
由△DEF∽△DBA知：∠DFE＝∠DAH，
∴sin∠DFE＝sin∠DAH＝＝＝．
8．（2022•荆州）如图1，在矩形ABCD中，AB＝4，AD＝3，点O是边AB上一个动点（不与点A重合），连接OD，将△OAD沿OD折叠，得到△OED；再以O为圆心，OA的长为半径作半圆，交射线AB于G，连接AE并延长交射线BC于F，连接EG，设OA＝x．
（1）求证：DE是半圆O的切线：
（2）当点E落在BD上时，求x的值；
（3）当点E落在BD下方时，设△AGE与△AFB面积的比值为y，确定y与x之间的函数关系式；
（4）直接写出：当半圆O与△BCD的边有两个交点时，x的取值范围．


【答案】（1）证明见解析部分；
（2）；
（3）y＝（0＜x＜）；
（4）＜x＜3或＜x≤4．
【解答】（1）证明：∵四边形ABCD是矩形，
∴∠DAO＝90°，
∵将△OAD沿OD折叠，得到△OED，
∴∠OED＝∠DAO＝90°，
∴OE⊥DE，
∵OE是半径，
∴DE是⊙O的切线；

（2）解：如图2中，当点E落在BD下方时，

在Rt△ADB中，∠DAB＝90°，AD＝3，AB＝4，
∴BD＝＝＝5，
∵S△ADB＝S△ADO+S△BDO，
∴×3×4＝×3×x+×5×x，
∴x＝．

（3）解：图2中，当点E落在BD上时，

∵DA＝DE，OA＝OE，
∴OD垂直平分线段AE，
∵•AD•AO＝•DO•AJ，
∴AJ＝，
∴AE＝2AJ＝，
∵AG是直径，
∴∠AEG＝∠ABF＝90°，
∵∠EAG＝∠BAF，
∴△AEG∽△ABF，
∴y＝＝（）2＝＝（0＜x＜）；

（4）当⊙O与CD相切时，x＝3，
当⊙O经过点C时，x2＝（4﹣x）2+32，
∴x＝，
观察图象可知，当＜x＜3或＜x≤4时，半圆O与△BCD的边有两个交点．
七．作图—复杂作图（共1小题）
9．（2022•荆州）如图，在10×10的正方形网格中，小正方形的顶点称为格点，顶点均在格点上的图形称为格点图形，图中△ABC为格点三角形．请按要求作图，不需证明．
（1）在图1中，作出与△ABC全等的所有格点三角形，要求所作格点三角形与△ABC有一条公共边，且不与△ABC重叠；
（2）在图2中，作出以BC为对角线的所有格点菱形．


【答案】（1）（2）作图见解析部分．
【解答】解：（1）如图1中，△ABD1，△ABD2，△ACD3，△ACD4，△CBD5即为所求；
（2）如图2中，菱形ABDC，菱形BECF即为所求．

八．作图—应用与设计作图（共1小题）
10．（2021•荆州）如图，在5×5的正方形网格图形中，小正方形的边长都为1，线段ED与AD的端点都在网格小正方形的顶点（称为格点）上．
请在网格图形中画图：
（1）以线段AD为边画正方形ABCD，再以线段DE为斜边画等腰直角三角形DEF，其中顶点F在正方形ABCD外；
（2）在（1）中所画图形基础上，以点B为其中一个顶点画一个新正方形，使新正方形的面积为正方形ABCD和△DEF面积之和，其它顶点也在格点上．

【答案】（1）（2）作图见解析部分．
【解答】解：（1）如图，正方形ABCD，△DEF即为所求．
（2）如图，正方形BKFG即为所求．

九．几何变换综合题（共1小题）
11．（2023•荆州）如图1，点P是线段AB上与点A，点B不重合的任意一点，在AB的同侧分别以A，P，B为顶点作∠1＝∠2＝∠3，其中∠1与∠3的一边分别是射线AB和射线BA，∠2的两边不在直线AB上，我们规定这三个角互为等联角，点P为等联点，线段AB为等联线．
（1）如图2，在5×3个方格的纸上，小正方形的顶点为格点、边长均为1，AB为端点在格点的已知线段．请用三种不同连接格点的方法，作出以线段AB为等联线、某格点P为等联点的等联角，并标出等联角，保留作图痕迹；
（2）如图3，在Rt△APC中，∠A＝90°，AC＞AP，延长AP至点B，使AB＝AC，作∠A的等联角∠CPD和∠PBD．将△APC沿PC折叠，使点A落在点M处，得到△MPC，再延长PM交BD的延长线于E，连接CE并延长交PD的延长线于F，连接BF．
①确定△PCF的形状，并说明理由；
②若AP：PB＝1：2，BF＝k，求等联线AB和线段PE的长（用含k的式子表示）．

【答案】（1）作图见解答．
（2）①△PCF是等腰直角三角形．理由见解答．
②等联线AB＝3k，线段PE＝．
【解答】解：（1）作图如下：（方法不唯一）

（2）①△PCF是等腰直角三角形．理由为：
如图，过点C作CN⊥BE交BE的延长线于N．

由折叠得AC＝CM，∠CMP＝∠CME＝∠A＝90°，∠1＝∠2，
∵AC＝AB，∠A＝∠PBD＝∠N＝90°，
∴四边形ABNC为正方形，
∴CN＝AC＝CM，
又∵CE＝CE，
∴Rt△CME≌Rt△CNE（HL），
∴∠3＝∠4，
而∠1+∠2+∠3+∠4＝90°，∠CPF＝90°，
∴∠PCF＝∠2+∠3＝∠CFP＝45°，
∴△PCF是等腰直角三角形．
②如图，过点F作FQ⊥BE于Q，FR⊥PB交PB的延长线于R，
则∠R＝∠A＝90°，

∵∠1+∠5＝∠5+∠6＝90°，
∴∠1＝∠6，
由△PCF是等腰直角三角形知：PC＝PF，
∴△APC≌△RFP（AAS），
∴AP＝FR，AC＝PR，
而AC＝AB，
∴AP＝BR＝FR，
在Rt△BRF中，BR2+FR2＝BF2，，
∴AP＝BR＝FR＝k，
∴PB＝2AP＝2k，
∴AB＝AP+PB＝BN＝3k，
∵BR＝FR，∠QBR＝∠R＝∠FQB＝90°，
∴四边形BRFQ为正方形，BQ＝OF＝k，
∵FQ⊥BN，CN⊥BN，
∴FQ∥CN，
∴，
而QE＝BN﹣NE﹣BQ＝3k﹣NE﹣k＝2k﹣NE，
∴，
解得：k，
由①知：PM＝AP＝k，，
∴，
答：等联线AB＝3k，线段PE＝．
一十．相似形综合题（共1小题）
12．（2021•荆州）在矩形ABCD中，AB＝2，AD＝4，F是对角线AC上不与点A，C重合的一点，过F作FE⊥AD于E，将△AEF沿EF翻折得到△GEF，点G在射线AD上，连接CG．
（1）如图1，若点A的对称点G落在AD上，∠FGC＝90°，延长GF交AB于H，连接CH．
①求证：△CDG∽△GAH；
②求tan∠GHC．
（2）如图2，若点A的对称点G落在AD延长线上，∠GCF＝90°，判断△GCF与△AEF是否全等，并说明理由．

【答案】（1）①证明过程见解答；
②；
（2）不全等，理由见解答．
【解答】（1）如图1，
①证明：∵四边形ABCD是矩形，
∴∠D＝∠GAH＝90°，
∴∠DCG+∠DGC＝90°，
∵∠FGC＝90°，
∴∠AGH+∠DGC＝90°，
∴∠DCG＝∠AGH，
∴△CDG∽△GAH．
②由翻折得∠EGF＝∠EAF，
∴∠AGH＝∠DAC＝∠DCG，
∵CD＝AB＝2，AD＝4，
∴＝tan∠DAC＝＝，
∴DG＝CD＝×2＝1，
∴GA＝4﹣1＝3，
∵△CDG∽△GAH，
∴，
∴tan∠GHC＝＝．
（2）不全等，理由如下：
∵AD＝4，CD＝2，
∴AC＝＝，
∵∠GCF＝90°，
∴＝tan∠DAC＝，
∴CG＝AC＝×2＝，
∴AG＝＝5，
∴EA＝AG＝，
∴EF＝EA•tan∠DAC＝＝，
∴AF＝＝，
∴CF＝2＝，
∵∠GCF＝∠AEF＝90°，而CG≠EA，CF≠EF，
∴△GCF与△AEF不全等．


一十一．解直角三角形的应用-仰角俯角问题（共1小题）
13．（2022•荆州）荆州城徽“金凤腾飞”立于古城东门外．如图，某校学生测量其高AB（含底座），先在点C处用测角仪测得其顶端A的仰角为32°，再由点C向城徽走6.6m到E处，测得顶端A的仰角为45°．已知B，E，C三点在同一直线上，测角仪离地面的高度CD＝EF＝1.5m，求城徽的高AB．（参考数据：sin32°≈0.530，cos32°≈0.848，tan32°≈0.625）．

【答案】城徽的高AB约为12.5米．
【解答】解：延长DF交AB于点G，

则∠AGF＝90°，DF＝CE＝6.6米，CD＝EF＝BG＝1.5米，
设FG＝x米，
∴DG＝FG+DF＝（x+6.6）米，
在Rt△AGF中，∠AFG＝45°，
∴AG＝FG•tan45°＝x（米），
在Rt△AGD中，∠ADG＝32°，
∴tan32°＝＝≈0.625，
∴x＝11，
经检验：x＝11是原方程的根，
∴AB＝AG+BG＝11+1.5＝12.5（米），
∴城徽的高AB约为12.5米．

一十二．列表法与树状图法（共1小题）
14．（2022•荆州）为弘扬荆州传统文化，我市将举办中小学生“知荆州、爱荆州、兴荆州”知识竞赛活动．某校举办选拔赛后，随机抽取了部分学生的成绩，按成绩（百分制）分为A，B，C，D四个等级，并绘制了如下不完整的统计图表．
等级
成绩（x）
人数
A
90＜x≤100
m
B
80＜x≤90
24
C
70＜x≤80
14
D
x≤70
10
根据图表信息，回答下列问题：
（1）表中m＝　12　；扇形统计图中，B等级所占百分比是 　40%　，C等级对应的扇形圆心角为 　84　度；
（2）若全校有1400人参加了此次选拔赛，则估计其中成绩为A等级的共有 　280　人；
（3）若全校成绩为100分的学生有甲、乙、丙、丁4人，学校将从这4人中随机选出2人参加市级竞赛．请通过列表或画树状图，求甲、乙两人至少有1人被选中的概率．

【答案】（1）12，40%，84；
（2）280；
（3）．
【解答】解：（1）抽取的学生人数为：10÷＝60（人），
∴m＝60﹣24﹣14﹣10＝12，
扇形统计图中，B等级所占百分比是：24÷60×100%＝40%，C等级对应的扇形圆心角为：360°×＝84°，
故答案为：12，40%，84；
（2）估计其中成绩为A等级的共有：1400×＝280（人），
故答案为：280；
（3）画树状图如下：

共有12种等可能的结果，其中甲、乙两人至少有1人被选中的结果有10种，
∴甲、乙两人至少有1人被选中的概率为＝．