初中数学人教版八年级下册20.2 数据的波动程度教学设计

数据的波动程度(1)

一、教学目标

(一)知识与技能：1.理解方差概念的产生和形成的过程；2.会用方差的计算公式来比较两组数据的波动大小；3.用方差对实际问题作出判断.

(二)过程与方法：学生通过本节课内容的学习，体会方差的形成过程，感受到方差是一种描述数据离散程度的统计量，并且根据方差的大小对实际问题作出分析，培养学生解决问题的能力.

(三)情感态度与价值观：以学生兴趣引出问题，在学习过程中培养学生观察问题、分析问题、解决问题的能力，通过对问题的不断深入探究，培养学生认真、耐心、细致的学习态度和学习习惯.

二、教学重点、难点

重点：1.掌握方差的定义和计算公式；2.会用方差公式进行计算，会比较数据的波动大小.

难点：理解方差的意义.

三、教学过程

教练的烦恼

现要从甲，乙两名射击选手中挑选一名射击选手参加比赛.若你是教练，你认为挑选哪一位比较合适？
甲，乙两名射击选手的测试成绩统计如下：

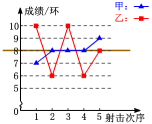(1)请分别计算两名选手的平均成绩；

(环)，(环)

(2)请根据这两名选手的成绩在右图中画出折线统计图；

(3)现要挑选一名选手参加比赛，若你是教练，你认为挑选哪一位比较适宜？为什么？

谁的稳定性好？应以什么数据来衡量？

甲射击成绩与平均成绩的偏差的和：(7-8)+(8-8)+(8-8)+(8-8)+(9-8)=0

乙射击成绩与平均成绩的偏差的和：(10-8)+(6-8)+(10-8)+(6-8)+(8-8)=0

怎么办？

甲射击成绩与平均成绩的偏差的平方和：(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2=2

乙射击成绩与平均成绩的偏差的平方和：(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=16

上述各偏差的平方和的大小还与什么有关？

——与射击次数有关！

所以要进一步用各偏差平方的平均数来衡量数据的稳定性.

为了刻画一组数据的波动大小，可以采用很多方法.统计中常采用下面的做法：设有n个数据x1，x2，…，xn，各数据与它们的平均数的差的平方分别是(x1-)2，(x2-)2，…，(xn-)2，我们用这些值的平均数，即用s2=[(x1-)2+(x2-)2+…+(xn-)2]来衡量这组数据的波动大小，并把它叫做这组数据的方差，记作s2.

方差：各数据与它们的平均数的差的平方的平均数.s2=[(x1-)2+(x2-)2+…+(xn-)2]

计算方差的步骤可概括为“先平均，后求差，平方后，再平均”.

方差如何反映数据波动情况呢？结合前面折线统计图及所求方差得出结论.

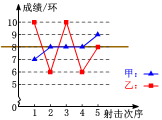
甲：(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2=2

乙：(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=16

，

当数据分布比较分散(即数据在平均数附近波动较大)时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小，方差就较小.反过来也成立，这样就可以用方差刻画数据的波动程度，即：方差越大，数据的波动越大；方差越小，数据的波动越小.

我们知道，用样本估计总体是统计的基本思想，正像用样本的平均数估计总体的平均数一样，考察总体方差时，如果所要考察的总体包含很多个体，或者考察本身带有破坏性时，实际中常常用样本的方差来估计总体的方差.

问题 农科院计划为某地选择合适的甜玉米种子.选择种子时，甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况，农科院各用10块自然条件相同的试验田进行试验，得到各试验田每公顷的产量(单位:t)如下表.

根据这些数据估计，农科院应该选择哪种甜玉米种子呢？

解：(1)为了直观地看出甲、乙两种甜玉米产量的情况，我们把这两组数据画成下面两幅图.

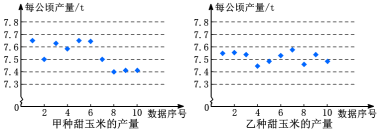
(2)甲、乙两个品种在试验田中的产量组成一个样本，算得样本数据的平均数为

，

说明在试验田中，甲、乙两种甜玉米的平均产量相差不大.由此可以估计在这个地区种植这两种甜玉米，它们的平均产量相差不大.

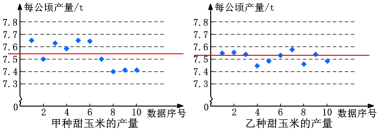
(3)两组数据的方差分别是

显然＞，即甲种甜玉米的波动大，这与我们从右图看到的结果是一致的.

由此可知，在试验田中，乙种甜玉米的产量比较稳定.正如用样本的平均数估计总体的平均数一样，也可以用样本的方差来估计总体的方差.因此可以推测，在这个地区种值乙种甜玉米的产量比甲种的稳定.综合考虑甲、乙两个品种的平均产量和产量的稳定性，可以推测这个地区比较适合种值乙种甜玉米.

例1 在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，参加表演的女演员的身高(单位:cm)如下表

哪个芭蕾舞团女演员的身高更整齐？

解：甲、乙两团演员的平均身高分别是

方差分别是

由＜可知，甲芭蕾舞团女演员的身高更整齐.

练习

1.用条形图表示下列各组数据，计算并比较它们的平均数和方差，体会方差是怎样刻画数据的波动程度的.
(1) 6　6　6　6　6　6　6  (2) 5　5　6　6　6　7　7
(3) 3　3　4　6　8　9　9  (4) 3　3　3　6　9　9　9

解：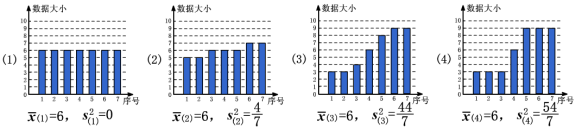

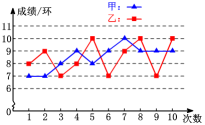2.如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图.观察图形，甲、乙这10次射击成绩的方差，哪个大？

解：甲、乙两射击运动员的平均成绩分别是(环)，(环)

方差分别是，

显然＜，即乙射击运动员的射击训练成绩波动大.

课堂小结

1.本节课你有哪些收获？2.还有没解决的问题吗？

四、教学反思

    通过这节课的教学，让我深刻的体会到只要我们充分相信学生，给学生以最大的自主探索空间，让学生经历数学知识的探究过程，这样既能让学生自主获取数学知识与技能，而且还能让学生达到对知识的深层次理解，更主要的是能让学生在探究过程中学习科学研究的方法，从而增强学生的自主意识，培养学生的探索精神和创新思维.