初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教案设计

这是一份初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教案设计，共3页。教案主要包含了教学目标，教学重点，教学过程，教学反思等内容，欢迎下载使用。
平行四边形的判定(1)一、教学目标(一)知识与技能：1.经历并了解平行四边形判别方法的探索过程，使学生逐步掌握说理的基本方法；2.探索并掌握平行四边形的判别方法，能根据判别方法进行有关的应用.(二)过程与方法：1.通过实验、观察、猜想、验证、推理、交流等探究活动，进一步培养学生的动手能力、合情推理能力；2.在运用平行四边形的判定方法解决问题的过程中，体验教学活动充满着探索性和挑战性，进一步培养和发展学生的逻辑思维能力和推理论证的表达能力.(三)情感态度价值观：1.经过自主探素与合作交流，敢于发表自己的观点，养成一种勇于探索、勇于质疑的精神及严密的数学逻辑推理论证的科学态度；2.体验数学活动来源于生活又服务于生活，提高学生的学习兴趣.二、教学重点、难点重点：掌握平行四边形的判定定理难点：综合运用平行四边形的性质与判定解决问题.三、教学过程知识回顾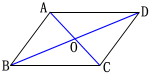平行四边形的性质：边：平行四边形的对边平行且相等；∵ 四边形ABCD是平行四边形
∴ AB∥CD，AD∥BC，AB=CD，AD=BC 角：平行四边形的对角相等；∵ 四边形ABCD是平行四边形 ，∴ ∠BAD=∠BCD，∠ABC=∠ADC对角线：平行四边形的对角线互相平分.∵ 四边形ABCD是平行四边形，∴ OA=OC，OB=OD思考    反过来，对边相等，或对角相等，或对角线互相平分的四边形是平行四边形吗？也就是说，平行四边形的性质定理的逆命题成立吗？    平行四边形判定定理1：两组对边分别相等的四边形是平行四边形    平行四边形判定定理2：两组对角分别相等的四边形是平行四边形    平行四边形判定定理3：对角线互相平分的四边形是平行四边形平行四边形判定定理1：两组对边分别相等的四边形是平行四边形(证明过程)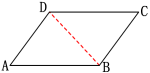如图，在四边形ABCD中，AB=CD，AD=CB.
求证：四边形ABCD是平行四边形.证明：连接BD.
∵ AB=CD，AD=CB，BD=DB
∴ △ABD≌△CDB (SSS)
∴ ∠ABD=∠CDB，∠ADB=∠CBD
∴ AB∥CD，AD∥CB
∴ 四边形ABCD是平行四边形几何符号语言：∵ AB=CD，AD=CB
∴ 四边形ABCD是平行四边形平行四边形判定定理2：两组对角分别相等的四边形是平行四边形(证明过程)如图，在四边形ABCD中，∠A=∠C，∠B=∠D.
求证：四边形ABCD是平行四边形.证明：∵ ∠A+∠B+∠C+∠D=360°
又 ∠A=∠C，∠B=∠D
∴ ∠A+∠D=180°，∠A+∠B=180°
∴ AB∥CD，AD∥CB
∴ 四边形ABCD是平行四边形几何符号语言：∵ ∠A=∠C，∠B=∠D
∴ 四边形ABCD是平行四边形平行四边形判定定理3：对角线互相平分的四边形是平行四边形(证明过程)如图，在四边形ABCD中，OA=OC，OB=OD.
求证：四边形ABCD是平行四边形.证明：∵ OA=OC，OB=OD，∠AOD=∠COB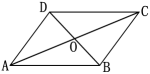
∴ △AOD≌△COB (SAS)
∴ ∠OAD=∠OCB
∴ AD∥BC
同理 AB∥DC
∴ 四边形ABCD是平行四边形几何符号语言：∵ OA=OC，OB=OD
∴ 四边形ABCD是平行四边形例3 如图，□ABCD的对角线AC、BD相交于点O，E、F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.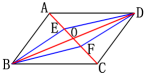证明：∵ 四边形ABCD是平行四边形
∴ AO=CO，BO=DO
∵ AE=CF
∴ AO-AE=CO-CF
即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形你还有其它证明方法吗？练习1.如图，AB=DC=EF，AD=BC，DE=CF，图中有哪些互相平行的线段？并说明理由.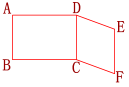答：AD∥BC，DE∥CF，AB∥DC∥EF.
理由：
∵ AB=DC，AD=BC
∴ 四边形ABCD是平行四边形
∴ AD∥BC，AB∥DC
∵ DC=EF，DE=CF
∴ 四边形DCFE是平行四边形
∴ DE∥CF，DC∥EF
因此，AD∥BC，DE∥CF，AB∥DC∥EF.2.如图，□ABCD的对角线AC，BD相交于点O，E，F分别是OA，OC的中点，求证BE=DF.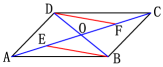证法1：∵ 四边形ABCD是平行四边形
∴ OA=OC，OB=OD
∵ E，F分别是OA，OC的中点
∴ OE=OA，OF=OC
∴ OE=OF
又 ∠BOE=∠DOF
∴ △BOE≌△DOF (SAS)
∴ BE=DF证法2：连接DE，BF.
∵ 四边形ABCD是平行四边形
∴ OA=OC，OB=OD
∵ E，F分别是OA，OC的中点
∴ OE=OA，OF=OC
∴ OE=OF
∴ 四边形DEBF是平行四边形
∴ BE=DF课堂小结1.本节课你有哪些收获？2.还有没解决的问题吗？四、教学反思在整个教学过程中，以学生看、想、议、练为主体，教师在学生仔细观察、类比、想象的基础上加以引导点拨. 判定方法是学生自己探讨发现的，因此，应用也就成了学生自发的需要. 在证明命题的过程中，学生自然将判定方法进行对比和筛选，或对一题进行多解，便于思维发散，不把思路局限在某一判定方法上.