初中数学青岛版八年级上册4.5 方差优质ppt课件

这是一份初中数学青岛版八年级上册4.5 方差优质ppt课件，共22页。PPT课件主要包含了平均数中位数众数，刻画两组数据集中程度，45s，能够进行比较，cm²，求数据的平均数，完成习题45等内容，欢迎下载使用。

1.了解离差和方差的定义和计算公式。2.理解方差概念的产生和形成的过程。3.会用方差计算公式来比较两组数据的波动大小。
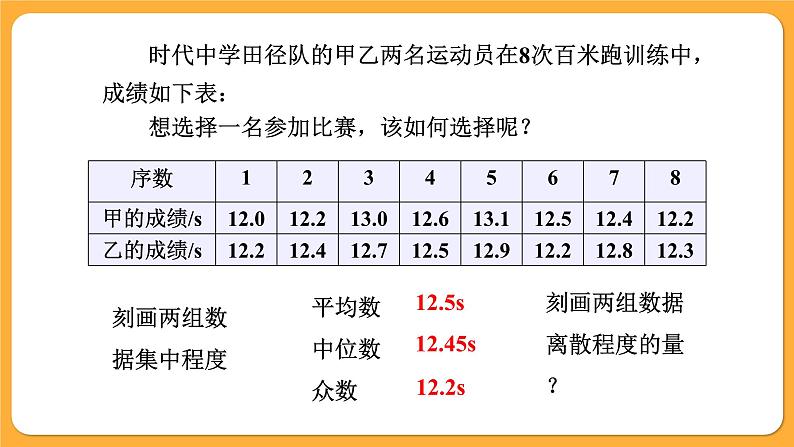
时代中学田径队的甲乙两名运动员在8次百米跑训练中，成绩如下表： 想选择一名参加比赛，该如何选择呢？
刻画两组数据离散程度的量？
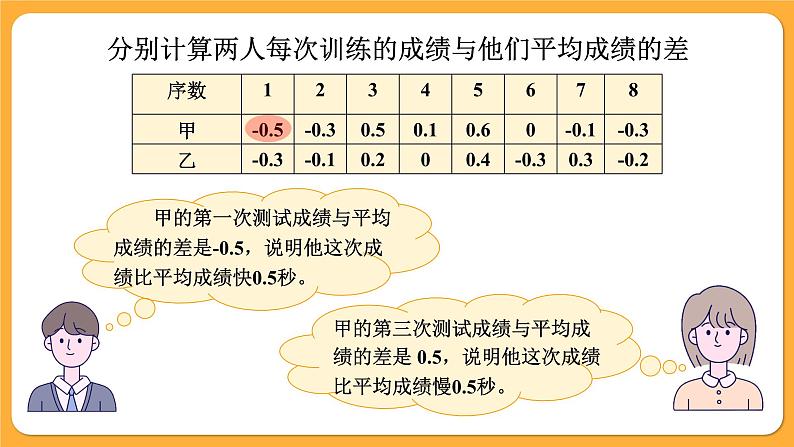
分别计算两人每次训练的成绩与他们平均成绩的差
在一组数据中，一个数据与这组数据的平均数的差叫做这个数据的离差。
离差可能是正数，负数，也可能是0。
离差的符号和大小反应了该数据偏离平均数的程度。
如何利用全部数据的离差来反应这组数据的离散程度呢？
用所有数据的离差之和表示一组数据的离散程度？
甲：-0.5-0.3+0.5+0.1+0.6+0-0.1-0.3=0.
乙：-0.3-0.1+0.2+0+0.4-0.3+0.3-0.2=0.
事实上，离差之和总是0。无法比较！
用所有数据的离差的绝对值之和表示一组数据的离散程度？
甲：|-0.5|+|-0.3|+0.5+0.1+0.6+0+|-0.1|+|-0.3|=3.4.
乙：|-0.3|+|-0.1|+0.2+0+0.4+|-0.3|+0.3+|-0.2|=1.8.
1.含绝对值不便于运算
2.离差个数不同导致错误的判断
为了刻画一组数据的离散程度，通常选用_________________________________来刻画这组数据的离散程度。
各个数据的离差的平方和的平均数
我们把它叫做这组数据的方差。
方差越大，说明数据的波动越大，越不稳定。
方差用来衡量一组数据的波动大小。(即这组数据偏离平均数的大小)。
计算方差的步骤可概括为“先平均，后求差，平方后，再平均”。
1.甲、乙两个运动员8次百米跑成绩的波动情况是（ ） A.甲的波动比乙大 B.乙的波动比甲大 C.甲、乙波动一样大 D.无法比较2.有5名同学目测同一本教科书的宽度时，产生的误差如下（单位：cm）：2，－2，－1，1，0。则这组数据的方差为________．
为了考察甲、乙两种小麦的长势，分别从中抽出10株苗，测得苗高如下(单位:cm): 甲: 12 13 14 15 10 16 13 11 15 11 乙: 11 16 17 14 13 19 6 8 10 16 问哪种小麦长得比较整齐?
思考：求数据方差的一般步骤是什么？
2.利用方差公式求方差。
解：1）计算甲的平均数和方差：
2）计算乙的平均数和方差：
所以，甲小麦长的比较整齐。
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小)。方差越大，说明数据的波动越大，越不稳定。
2.方差:各数据与它们的平均数的差的平方的平均数。
1.离差是一个数据与这组数据的平均数的差。
离差可能是正数，负数，也可能是0。离差的符号和大小反应了该数据偏离平均数的程度。
例1：甲、乙两位车工同时加工一种球形零件，图纸规定球形零件的直径为(15±0.05)mm，两人的工作效率相同。现从他们加工的零件中分别随机抽取5个进行检验，测得零件的直径如下(精确到0.01 mm):甲加工的零件：15.05，15.02，14.97，14.96，15.00乙加工的零件：15.00，15.01，15.02，14.97，15.00(1)分别求两个样本的平均数与方差；(2)如果从两人中推荐一人参加即将举办的全厂技术比赛，你认为应该派谁参加？
解：(1)分别计算样本的平均数和方差:
(2)比较两个样本，它们都在规定的(15±0.05)mm的范围内，并且平均数相等，但方差S2甲> S2乙，因而估计在他们加工的所有零件中，乙加工的零件的直径较稳定，所以应推荐乙参加比赛。
例2：某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示
（1）分别求出甲、乙两公司去年一至十月份汽车销售量的平均数、方差中位数和众数；（2）试从平均数和方差对甲、乙两公司的销售情况加以分析;（3）根据折线统计图，分析两家公司该品牌汽车销售量的变化趋势。
解：(1) 为了方便，先将统计图表达的甲、乙两家公司十个月销售该品牌的汽车的两组数据(单位：辆) 填入下面的表中，再分别求出它们的平均数、方差、中位数和众数:
(2)从平均数分析，两家公司的月平均销售量都是9辆，但是二者的方差相差很大，后者约为前者的 3 倍，造成这种差异的原因是乙公司的数据比较分散，有较多的数据(如3，4，5，13，13，16) 偏离平均数9的程度大;
(3)从折线图看，年初乙公司的销售情况明显低于甲公司，从三月份开始甲、乙两公司的销售水平开始接近，从六月份开始超过甲公司，以后各月销售量均比甲公司高，这表明在该品牌汽车的销售情况乙公司较有潜力。