广东省深圳市龙华区2022-2023学年八年级下学期期末数学试题（含答案）

保密★启用前

龙华区中小学2022-2023学年第二学期期末学业质量监测试卷

八年级数学

说明：

1.答题前，请将姓名、准考证号和学校用黑色字迹的钢笔或签字笔填写在答题卡指定的位置上，并将条形码粘贴好，不得在其它地方作任何标记.

2.试题卷共6页，答题卡共4页.考试时间为90分钟，满分120分.

3.作答选择题1~10，选出每题答案后，用2B铅笔把答题卡上对应题目答案标号的信息点框涂黑.如需改动，用橡皮擦干净后，再填涂其他答案.作答非选择题11~25，用黑色字迹的钢笔或签字笔将答案（含作辅助线）写在答题卡指定区域内.写在本试卷或草稿纸上，其答案一律无效.

4.考试结束后，请将答题卡交回.

第一部分  选择题

一、选择题（本大题共有10小题，每小题3分，共30分，每小题有四个选项，其中只有一个是正确的.）

1.“琴棋书画”的棋是指围棋，围棋起源于中国，至今已有四千多年的历史.下列由黑、白棋子摆成的图案中，是中心对称图形的是（    ）

A. B. C. D.

2.若，下列不等式变形，不一定成立的是（    ）

A.  B.

C.  D.

3.下列分式中，是最简分式的是（    ）

A. B. C. D.

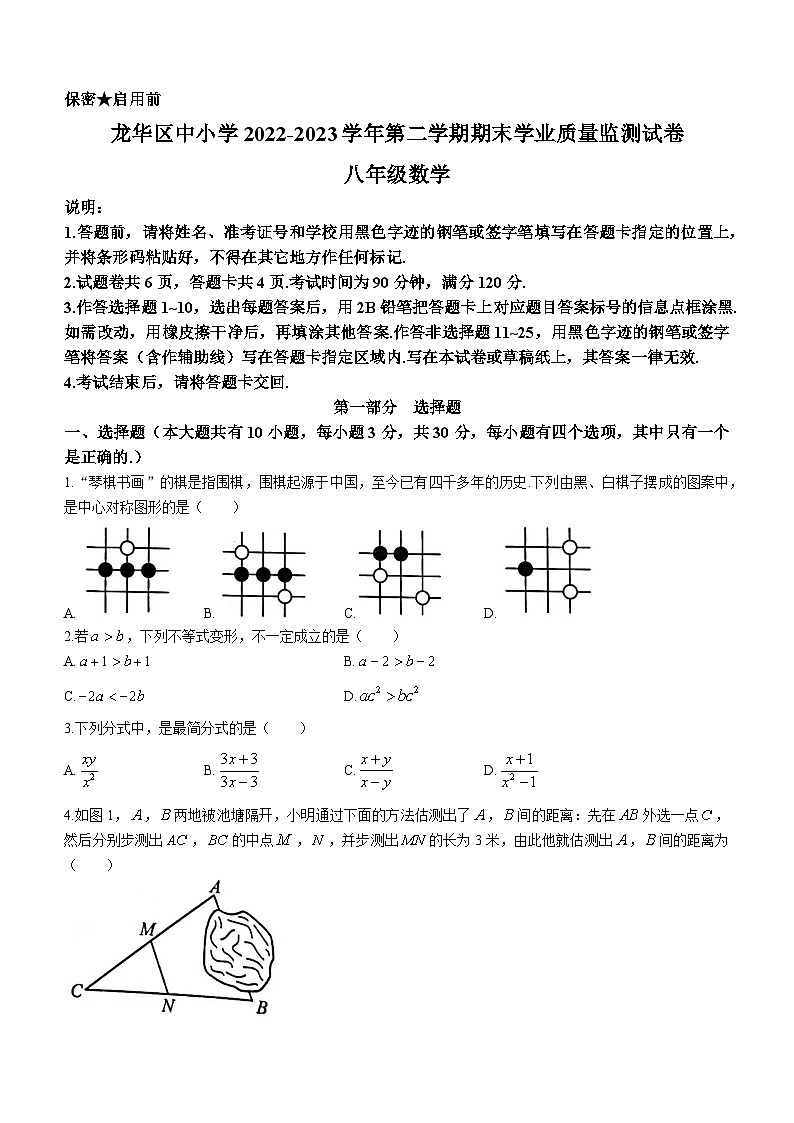
4.如图1，，两地被池塘隔开，小明通过下面的方法估测出了，间的距离：先在外选一点，然后分别步测出，的中点，，并步测出的长为3米，由此他就估测出，间的距离为（    ）

A.3米 B.4.5米 C.6米 D.9米

5.已知，，则多项式的值为（    ）

A.30 B.11 C.1 D.

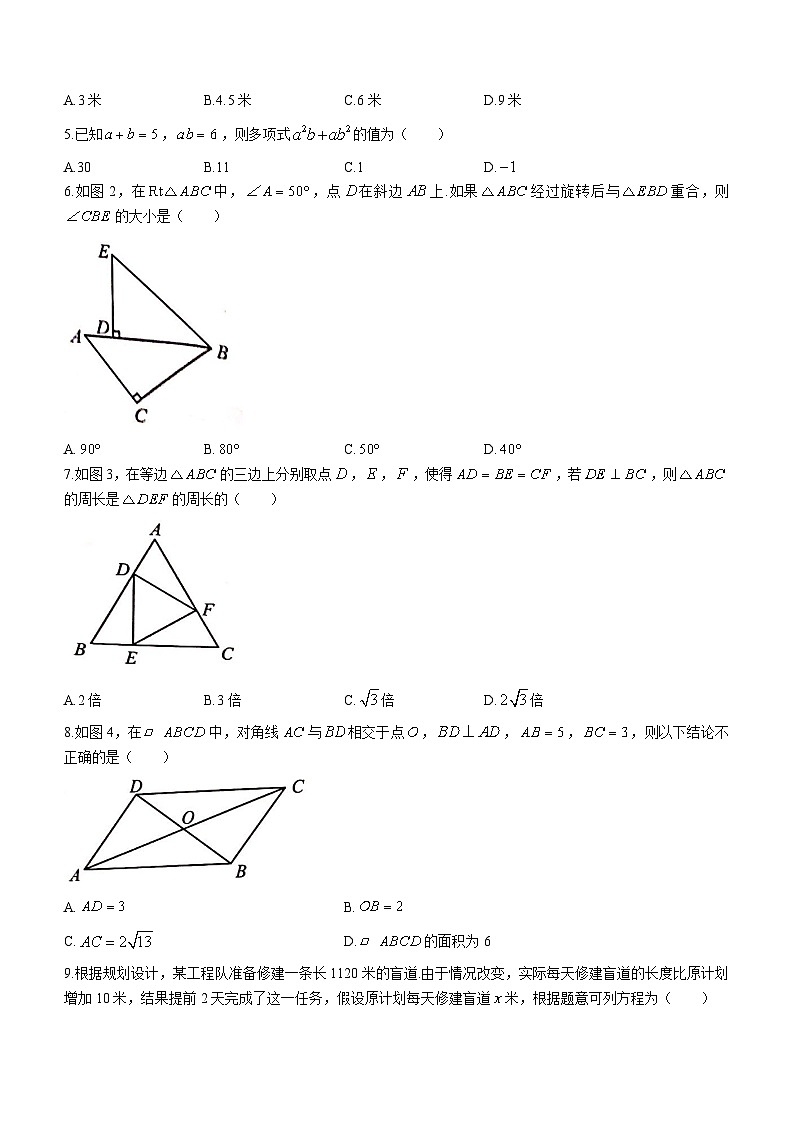
6.如图2，在中，，点在斜边上.如果经过旋转后与重合，则的大小是（    ）

A. B. C. D.

7.如图3，在等边的三边上分别取点，，，使得，若，则的周长是的周长的（    ）

A.2倍 B.3倍 C.倍 D.倍

8.如图4，在中，对角线与相交于点，，，，则以下结论不正确的是（    ）

A.  B.

C.  D.的面积为6

9.根据规划设计，某工程队准备修建一条长1120米的盲道.由于情况改变，实际每天修建盲道的长度比原计划增加10米，结果提前2天完成了这一任务，假设原计划每天修建盲道米，根据题意可列方程为（    ）

A.  B.

C.  D.

10.如图5，，直线与直线之间的距离为4，点是直线与外一点，点到直线的距离为2，点，分别是直线与直线上的动点，以点为圆心，的长为半径作弧，再以点为圆心，的长为半径作弧，两弧交于点，则点与点之间距离的最小值为（    ）

A.6 B.8 C.10 D.12

第二部分  非选择题

二、填空题（本大题共7小题，每小题3分，共21分.）

11.分解因式：______.

12.由深圳到广州的一条铁路全程约为146千米，高铁全程运行时间为小时，则高铁的速度是每小时______千米.

13.一个多边形的内角和等于它的外角和，则这个多边形是______边形.

14.一次函数的图像如图6所示，则不等式的解集为______.

15.某校学生会组织七年级和八年级共30名同学参加环保志愿者活动，七年级学生平均每人收集15个废弃塑料瓶，八年级学生平均每人收集20个废弃塑料瓶，为了保证所收集的塑料瓶总数不少于500个，则七年级学生参加活动的人数至多是______名

16.我们把顶角为的等腰三角形称作“黄金三角形”，“黄金三角形”的底边长是腰长的倍.如图7，是“黄金三角形”，，的垂直平分线交于点，交于点，则与的面积比为______.

16.如图8，在四边形中，，，将边绕点顺时针旋转后，点恰好落在边上的点处，已知，则的长度为______.

三、解答题（本大题共8小题，共69分.）

18.（8分）解不等式组：并把它的解集表示在数轴上.

19.（8分）先化简，再求值：，其中.

20.（7分）解方程：.

21.（6分）如图9，在平面直角坐标系中，的三个顶点，，的坐标分别是，，，若经过一次平移后得到，点，，的对应点分别为点，，，已知点的坐标为.根据以上条件，请解决下列问题：

（1）请画出平移后的；

（2）______（填“>”或“=”或“<”）；

（3）在平移过程中，边扫过的面积为______

22.（10分）已知四边形为平行四边形，点，分别是直线，上的点，且与点，，，不重合.

（1）请在图10中画出你设计的图形，并添加一个适当的条件：____________，使得点，与的两个顶点组成的四边形是一个平行四边形，并说明理由；

（2）如图11，已知，，若四边形为平行四边形，且，则的长度为______

图10  图11

23.（8分）某服装店老板用4000元购进了一批甲款恤，用8800元购进了一批乙款恤，已知所购乙款恤数量是甲款恤数量的2倍，购进的乙款恤单价比甲款恤单价贵5元.

（1）购进甲、乙两款恤的单价分别是多少元？

（2）老板把这两种恤的标价都定为每件100元，甲款恤打九折销售，乙款恤按标价销售.经过一段时间的销售，老板发现，销售两种恤共100件时，利润不低于4200元.那么这段时间按标价销售的乙款恤至少要销售多少件？

24.（10分）

【定义】对于没有公共点的两个图形，，点是图形上任意一点，点是图形上任意一点，把、两点之间的距离的最小值称为图形与图形的距离，记为.

【理解】如图12，在平面直角坐标系中，的对角线，相交于点，若点，的坐标分别为，，点是边上任意一点.

（1）当点在边上时，的最小值是______，因此[点，线段]=______；

（2）当点在任意边上时，的最小值是______，因此[点，]=______；

【拓展】如图13，在平面直角坐标系中，的对角线，相交于点，，平分，点，的坐标分别为，，点是对角线上与点，，不重合的一点，点是对角线上与点，，不重合的一点.

（3）当[线段，]时，则的取值范围为______；

（4）当时，______（结果用含的式子表示）；

【应用】为庆祝母亲节，某商场在广场举行花卉展览，要在长6米，宽4米的长方形花卉展览区外围用彩绳拉出封闭隔离线，要求封闭隔离线与长方形花卉展览区外围的最小距离均为0.5米，请直接写出所需彩绳的长度.

图12  图13 备用图

25.（12分）

【问题背景】如图14，在中，.将绕点逆时针旋转至，记旋转角，当线段与不共线时，记的面积为，的面积为.

图14  图15

【特例分析】如图15，当恰好过点，且点，，在同一条直线上时.

（1）______°；

（2）若，则______，______；

【推广探究】某数学兴趣小组经过交流讨论，猜想：在旋转过程中，与之间存在一定的等量关系.再经过独立思考，获得了如下一些解决思路：

思路1：如图16，过点，分别作直线平行于，，两直线交于点，连接，可证一组三角形全等，再根据平行四边形的相关性质解决问题；

思路2：如图17，过点作于点，过点作，交的延长线于点，可证一组三角形全等，再根据旋转的相关性质解决问题；

……

（3）如图18，请你根据以上思路，并结合你的想法，探究与之间的等量关系为______，并说明理由.

图16  图17  图18

【拓展应用】在旋转过程中，当为面积的时，的值为______

备用图

2022-2023学年第二学期八年级调研卷

参考答案及评分建议

一、选择题

BDCCA BCDAB

（说明：每小题3分，共30分.）

二、填空题

11. 12. 13.四 14. 15.20

16. 17.（说明：每小题3分，共21分．）

（17题提示：过点作交延长线于点，连接，∵，，∴，∴，可证，∴，∴为等腰直角三角形，∴，∴，∴）

三、解答题

18.（8分）解不等式组：

解：解不等式①得

解不等式②得

在同一数轴上表示解集如下：

∴原不等式组的解集为

19.（8分）解：原式（2个因式分解各1分，化乘法1分）

当时，原式

20.（7分）解：两边同乘以得：

解得：

经检验，是原分式方程的增根

∴原分式方程无解

21.（6分）

（1）如图所示

（2）=

（3）16

22.（10分）

（1）

补充条件：，

证明如下：

∵四边形是平行四边形

∴

∴

∵

∴四边形是平行四边形

（做法不唯一，言之有理即可，参照此标准酌情给分）

（2）6

23.（8分）

（1）解：设甲款T恤单价为元，则乙款T恤单价为元

依题意得：

解得：

经检验，是原方程的解

∴

答：甲款恤单价为50元，乙款恤单价为55元

（检验和答共计1分，写全才给）

（2）解：依题意得：甲售价（元/件）

设销售乙款T恤件

依题意得：

解得：

∴乙款T恤至少要销售40件

答：乙款恤至少要销售40件

24.（10分）【理解】（1）4；4

（2）3；3

【拓展】（3）或

（4）

【应用】所需彩绳长度为米

25.（12分）

【特例分析】（1）60

（2）；

【推广探究】（3）解：，理由如下：

思路1：如图，过点，分别作直线平行于，，两直线交于点，连接

∵，

∴四边形为平行四边形

∴，

∵旋转

∴，，

∴

∵

∴

∴

在和中

∴

∴

∵

∴

∴.

思路2：如图，过点作交延长线于点，过点作交延长线于点

∵，

∴

∵旋转

∴，，，

∴

∴

∴

即

在和中

∴

∴

∴

【拓展应用】（3）60或120（答对一个给1分）