人教版八年级上册13.4课题学习 最短路径问题示范课ppt课件

这是一份人教版八年级上册13.4课题学习 最短路径问题示范课ppt课件，共34页。PPT课件主要包含了知识回顾，学习目标，课堂导入，新知探究，跟踪训练，知识点两线一点型，随堂练习，BP+EP的最小值，最短路径问题，两线一点型等内容，欢迎下载使用。
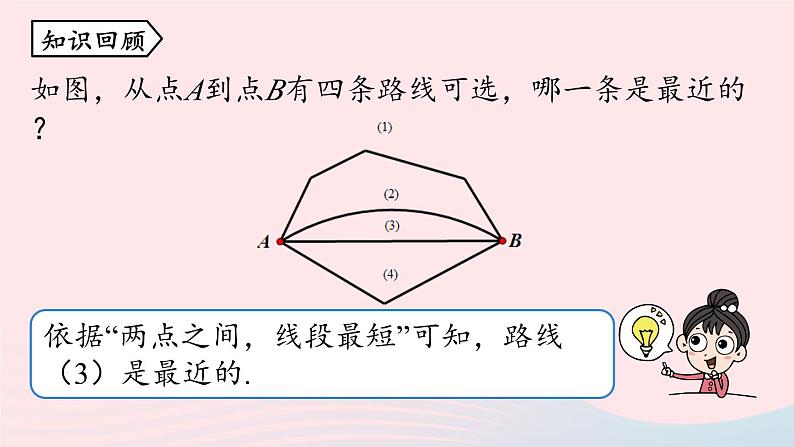
如图，从点A到点B有四条路线可选，哪一条是最近的？
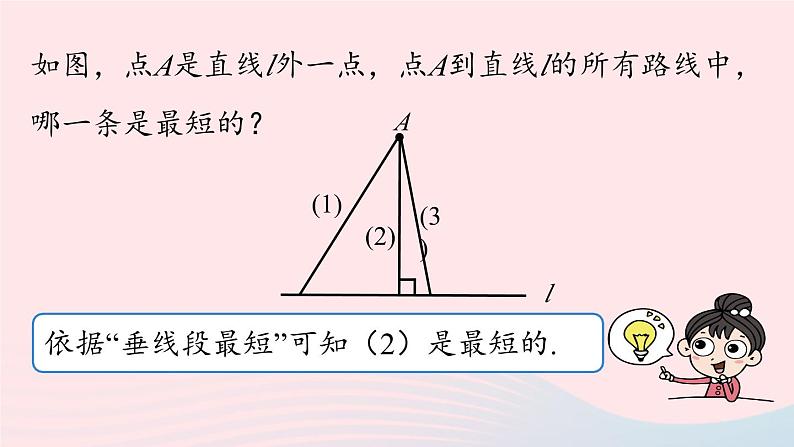
如图，点A是直线l外一点，点A到直线l的所有路线中，哪一条是最短的？
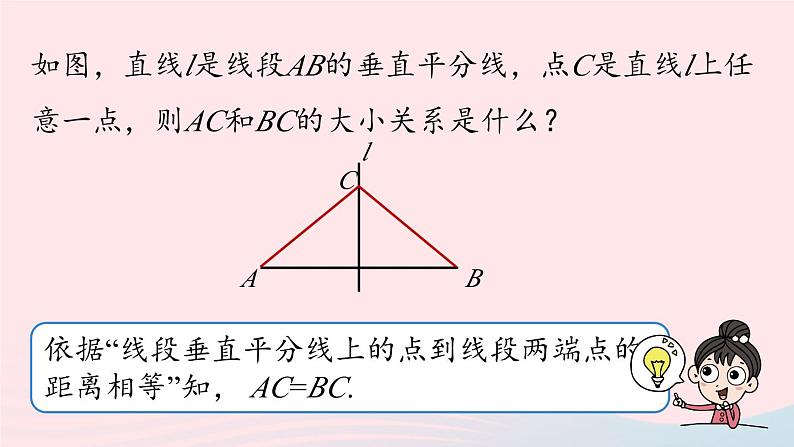
如图，直线l是线段AB的垂直平分线，点C是直线l上任意一点，则AC和BC的大小关系是什么？
1.利用轴对称,平移等变化解决简单的最短路径问题.2.体会图形的变化在解决最值问题中的作用,感受由实际问题转化为数学问题的思想.
相传古希腊亚历山大城里有一位久负盛名的学者，名叫海伦.有一天，一位将军专程拜访海伦，请教一个百思不得其解的问题：将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的B地开会，应该怎样走才能使路程最短？从此这个被称为“将军饮马”的问题广泛流传.
这是个实际问题，你能用自己理解的语言描述一下吗？
如图所示，将A，B 两地抽象为两个点，将河l抽象为一条直线.
知识点1 两点一线型
如图： 点A，B在直线l的同侧，点C是直线l上的一个动点，当点C在什么位置的时候，AC+BC的值最小？
作图问题：在直线 l 上求作一点C，使AC+BC最短．
解析：连接A，B两点，交直线l于点C，则点C即为所求的位置，可以使得AC+BC的值最小.依据：两点之间，线段最短.
如图，点A，B分别在直线l的两侧，点C是直线l上的一个动点，当点C在什么位置的时候，AC+BC的值最小？
你能利用两点分别在直线两侧的解题思路，来解决两点在直线同一侧的问题吗？
分析：如果我们能够把点B转移到直线l的另外一侧B′，同时使得对直线上任意一点C，满足BC=B′C，就可以将问题转化为“两点分别在直线两侧的情况”.那么在直线l上使得满足BC=B′C的点应该怎么找呢？
如图，作出点B关于直线l的对称点B′，利用轴对称的性质可知：对于直线l上的任意一点C均满足BC=B′C.此时，问题转化为：当点C在直线l的什么位置时，AB+B′C的值最小？
容易得出：连接AB′交直线l于点C，则点C即为所求.
证明：在直线l上任意取一点C′（不与点C重合），连接AC′，BC′，B′C′.由轴对称的性质可得：BC=B′C，BC′=B′C′，则AC+BC=AC+B′C=AB′，AC′+BC′=AC′+B′C′.在△AB′C′中，AB′