
江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-03选择题提升题
展开江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-03选择题提升题
【考点目录】
一.多项式乘多项式(共1小题) 1
四.等腰三角形的性质(共1小题) 2
五.勾股定理(共2小题) 2
六.平行四边形的性质(共1小题) 3
七.矩形的性质(共1小题) 3
八.正方形的性质(共1小题) 3
九.切线的性质(共2小题) 4
一十.扇形面积的计算(共1小题) 4
一十一.圆锥的计算(共1小题) 5
一十二.相似三角形的性质(共1小题) 5
一十三.相似三角形的判定(共1小题) 5
一十四.方差(共1小题) 5
【专题练习】
一. 多项式乘多项式(共1小题)
1.(2022•南通)已知实数m,n满足m2+n2=2+mn,则(2m﹣3n)2+(m+2n)(m﹣2n)的最大值为( )
A.24 B. C. D.﹣4
二. 反比例函数图象上点的坐标特征(共1小题)
2.(2022•宿迁)如图,点A在反比例函数y=(x>0)的图象上,以OA为一边作等腰直角三角形OAB,其中∠OAB=90°,AO=AB,则线段OB长的最小值是( )
A.1 B. C.2 D.4
三. 二次函数的最值(共1小题)
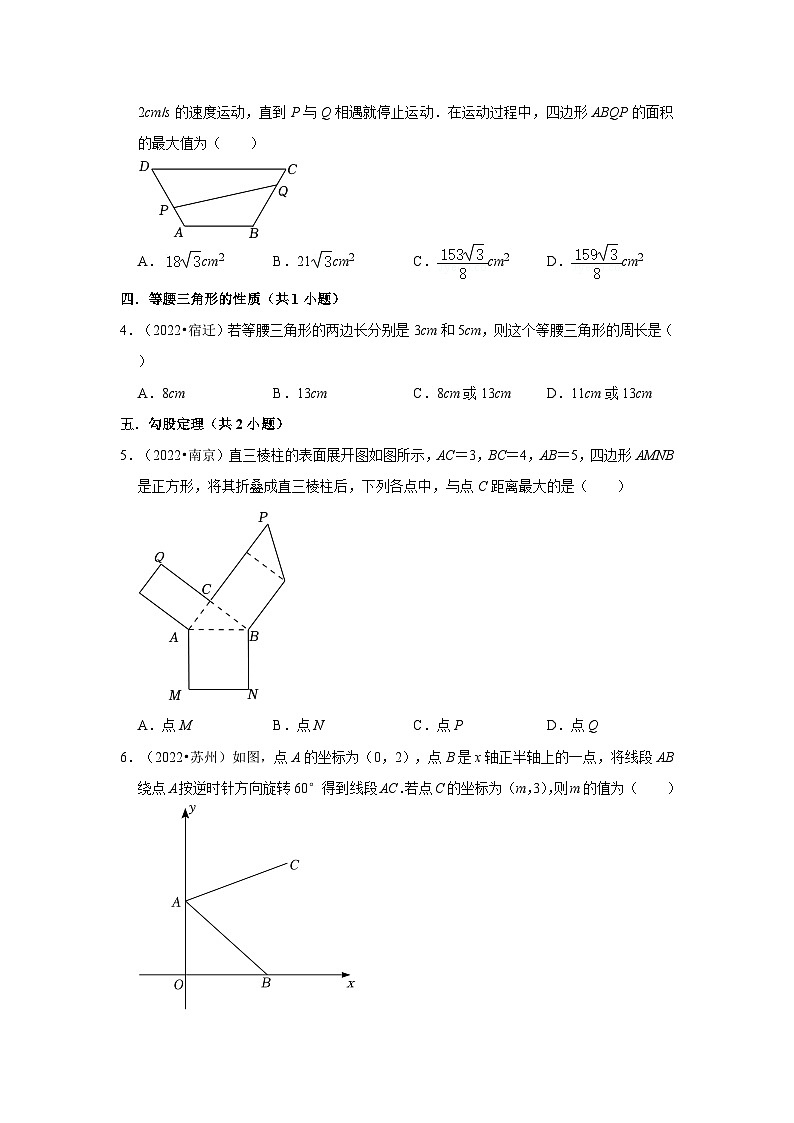
3.(2022•无锡)在四边形ABCD中,AB∥DC,∠C=∠D=60o,AB=6cm,CD=12cm,点P从A点出发,沿A→D→C以1cm/s的速度运动;点Q从B点出发,沿B→C→D以2cm/s的速度运动,直到P与Q相遇就停止运动.在运动过程中,四边形ABQP的面积的最大值为( )
A.cm2 B.21cm2 C.cm2 D.cm2
四.等腰三角形的性质(共1小题)
4.(2022•宿迁)若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )
A.8cm B.13cm C.8cm或13cm D.11cm或13cm
五.勾股定理(共2小题)
5.(2022•南京)直三棱柱的表面展开图如图所示,AC=3,BC=4,AB=5,四边形AMNB是正方形,将其折叠成直三棱柱后,下列各点中,与点C距离最大的是( )
A.点M B.点N C.点P D.点Q
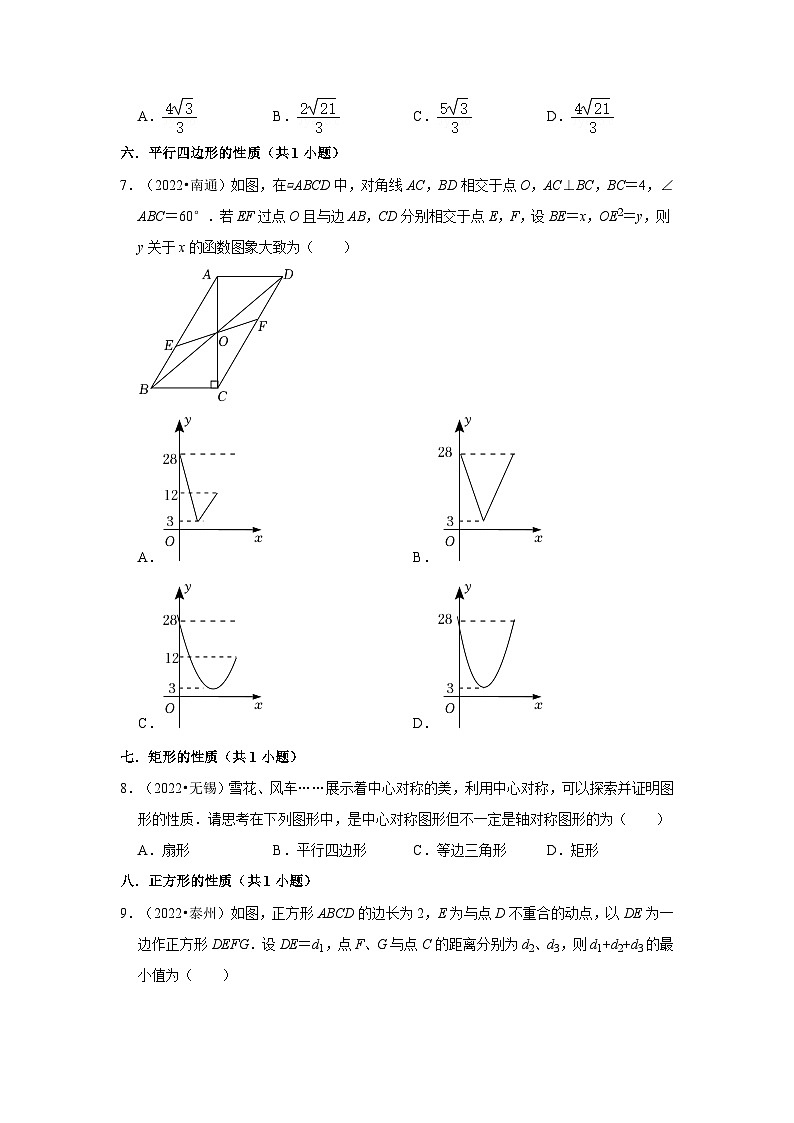
6.(2022•苏州)如图,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为(m,3),则m的值为( )
A. B. C. D.
六.平行四边形的性质(共1小题)
7.(2022•南通)如图,在▱ABCD中,对角线AC,BD相交于点O,AC⊥BC,BC=4,∠ABC=60°.若EF过点O且与边AB,CD分别相交于点E,F,设BE=x,OE2=y,则y关于x的函数图象大致为( )
A. B.
C. D.
七.矩形的性质(共1小题)
8.(2022•无锡)雪花、风车……展示着中心对称的美,利用中心对称,可以探索并证明图形的性质.请思考在下列图形中,是中心对称图形但不一定是轴对称图形的为( )
A.扇形 B.平行四边形 C.等边三角形 D.矩形
八.正方形的性质(共1小题)
9.(2022•泰州)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为( )
A. B.2 C.2 D.4
九.切线的性质(共2小题)
10.(2022•镇江)如图,在等腰△ABC中,∠BAC=120°,BC=6,⊙O同时与边BA的延长线、射线AC相切,⊙O的半径为3.将△ABC绕点A按顺时针方向旋转α(0°<α≤360°),B、C的对应点分别为B′、C′,在旋转的过程中边B′C′所在直线与⊙O相切的次数为( )
A.1 B.2 C.3 D.4
11.(2022•无锡)如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )
A.AE⊥DE B.AE∥OD C.DE=OD D.∠BOD=50°
一十.扇形面积的计算(共1小题)
12.(2022•连云港)如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A.π﹣ B.π﹣ C.π﹣2 D.π﹣
一十一.圆锥的计算(共1小题)
13.(2022•无锡)在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )
A.12π B.15π C.20π D.24π
一十二.相似三角形的性质(共1小题)
14.(2022•连云港)△ABC的三边长分别为2,3,4,另有一个与它相似的三角形DEF,其最长边为12,则△DEF的周长是( )
A.54 B.36 C.27 D.21
一十三.相似三角形的判定(共1小题)
15.(2022•连云港)如图,将矩形ABCD沿着GE、EC、GF翻折,使得点A、B、D恰好都落在点O处,且点G、O、C在同一条直线上,同时点E、O、F在另一条直线上.小炜同学得出以下结论:①GF∥EC;②AB=AD;③GE=DF;④OC=2OF;⑤△COF∽△CEG.其中正确的是( )
A.①②③ B.①③④ C.①④⑤ D.②③④
一十四.方差(共1小题)
16.(2022•镇江)第1组数据为:0、0、0、1、1、1,第2组数据为:、,其中m、n是正整数下列结论:①当m=n时,两组数据的平均数相等;②当m>n时,第1组数据的平均数小于第2组数据的平均数;③当m<n时,第1组数据的中位数小于第2组数据的中位数;④当m=n时,第2组数据的方差小于第1组数据的方差.其中正确的是( )
A.①② B.①③ C.①④ D.③④
江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-03选择题提升题
参考答案与试题解析
一.多项式乘多项式(共1小题)
1.(2022•南通)已知实数m,n满足m2+n2=2+mn,则(2m﹣3n)2+(m+2n)(m﹣2n)的最大值为( )
A.24 B. C. D.﹣4
【答案】B
【解答】解:方法1、∵m2+n2=2+mn,
∴(2m﹣3n)2+(m+2n)(m﹣2n)
=4m2+9n2﹣12mn+m2﹣4n2
=5m2+5n2﹣12mn
=5(mn+2)﹣12mn
=10﹣7mn,
∵m2+n2=2+mn,
∴(m+n)2=2+3mn≥0(当m+n=0时,取等号),
∴mn≥﹣,
∴(m﹣n)2=2﹣mn≥0(当m﹣n=0时,取等号),
∴mn≤2,
∴﹣≤mn≤2,
∴﹣14≤﹣7mn≤,
∴﹣4≤10﹣7mn≤,
即(2m﹣3n)2+(m+2n)(m﹣2n)的最大值为,
故选:B.
方法2、设m+n=k,则m2+2mn+n2=k2,
∴mn+2+2mn=k2,
∴mn=k2﹣,
∴原式=10﹣7mn=﹣k2+≤,
故选:B.
二.反比例函数图象上点的坐标特征(共1小题)
2.(2022•宿迁)如图,点A在反比例函数y=(x>0)的图象上,以OA为一边作等腰直角三角形OAB,其中∠OAB=90°,AO=AB,则线段OB长的最小值是( )
A.1 B. C.2 D.4
【答案】C
【解答】解:∵三角形OAB是等腰直角三角形,
∴当OB最小时,OA最小,
设A点坐标为(a,),
∴OA=,
∵≥0,
即:﹣4≥0,
∴≥4,
∵≥0,
两边同时开平方得:a﹣=0,
∴当a=时,OA有最小值,
解得a1=,a2=﹣(舍去),
∴A点坐标为(,),
∴OA=2,
∵三角形OAB是等腰直角三角形,OB为斜边,
∴OB=OA=2.
解法二:OB最小时,OA最小,此时OA是到图象上的最近距离,OA的解析式是y=x,
故A(,),
∴OA的最小值为2,
∴OB的最小值为2.
故选:C.
三.二次函数的最值(共1小题)
3.(2022•无锡)在四边形ABCD中,AB∥DC,∠C=∠D=60o,AB=6cm,CD=12cm,点P从A点出发,沿A→D→C以1cm/s的速度运动;点Q从B点出发,沿B→C→D以2cm/s的速度运动,直到P与Q相遇就停止运动.在运动过程中,四边形ABQP的面积的最大值为( )
A.cm2 B.21cm2 C.cm2 D.cm2
【答案】C
【解答】解:如图1,
作AE⊥CD于E,作BF⊥CD于F,
∴∠BFE=∠AEF=90°,
∴AE∥BF,
∵AB∥CD,
∴四边形AEFB是平行四边形,
∴▱AEFB是矩形,
∴EF=AB=6,AE=BF,
∵∠C=∠D,
∴△AED≌△BFC(AAS),
∴DE=CF=3,
∴AD=BC=2CF=6,AE=BF=3,
∴梯形ABCD的面积S==27,
如图2,
当点Q在BC上时,
当点Q和点C重合时,四边形ABQP的面积最大.此时AP=PQ=3,
∴四边形ABQP的面积=27﹣=18,
如图3,
当点Q在CD上,点P在AD上时,设四边形ABQP的面积为S,
∵==,
S△PDQ=,
∴S=27=,
∴当t=时,S最大=,
因为,
故选:C.
四.等腰三角形的性质(共1小题)
4.(2022•宿迁)若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )
A.8cm B.13cm C.8cm或13cm D.11cm或13cm
【答案】D
【解答】解:当3cm是腰长时,3,3,5能组成三角形,
当5cm是腰长时,5,5,3能够组成三角形.
则三角形的周长为11cm或13cm.
故选:D.
五.勾股定理(共2小题)
5.(2022•南京)直三棱柱的表面展开图如图所示,AC=3,BC=4,AB=5,四边形AMNB是正方形,将其折叠成直三棱柱后,下列各点中,与点C距离最大的是( )
A.点M B.点N C.点P D.点Q
【答案】B
【解答】解:如图,过C点作CE⊥AB于E,
∵AC=3,BC=4,AB=5,32+42=52,
∴△ACB是直角三角形,
∴CE=AC•BC÷÷AB=3×4÷5=2.4,
∴AE===1.8,
∴BE=5﹣1.8=3.2,
∵四边形AMNB是正方形,立方体是直三棱柱,
∴CQ=5,
∴CM=CP==,
CN==,
∵>>5,
∴与点C距离最大的是点N.
故选:B.
6.(2022•苏州)如图,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为(m,3),则m的值为( )
A. B. C. D.
【答案】C
【解答】解:过C作CD⊥x轴于点D,CE⊥y轴于点E,如图:
∵CD⊥x轴,CE⊥y轴,∠DOE=90°,
∴四边形EODC是矩形,
∵将线段AB绕点A按逆时针方向旋转60°得到线段AC,
∴AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴AB=AC=BC,
∵A(0,2),C(m,3),
∴CE=m=OD,CD=3,OA=2,
∴AE=OE﹣OA=CD﹣OA=1,
∴AC===BC=AB,
在Rt△BCD中,BD===,
在Rt△AOB中,OB===,
∵OB+BD=OD=m,
∴+=m,
化简变形得:3m4﹣22m2﹣25=0,
解得m=或m=﹣(舍去),
∴m=,
故选:C.
六.平行四边形的性质(共1小题)
7.(2022•南通)如图,在▱ABCD中,对角线AC,BD相交于点O,AC⊥BC,BC=4,∠ABC=60°.若EF过点O且与边AB,CD分别相交于点E,F,设BE=x,OE2=y,则y关于x的函数图象大致为( )
A. B.
C. D.
【答案】C
【解答】解:过O点作OM⊥AB于M,
∵AC⊥BC,∠ABC=60°,
∴∠BAC=30°,
∵BC=4,
∴AB=8,AC=,
∵四边形ABCD为平行四边形,
∴AO=AC=,
∴OM=AO=,
∴AM=,
设BE=x,OE2=y,则EM=AB﹣AM﹣BE=8﹣3﹣x=5﹣x,
∵OE2=OM2+EM2,
∴y=(x﹣5)2+3,
∴抛物线开口方向向上,顶点坐标为(5,3),与y轴的交点为(0,28),
∵0≤x≤8,
∴当x=8时y=12,
故符合解析式的图象为:
故选:C.
七.矩形的性质(共1小题)
8.(2022•无锡)雪花、风车……展示着中心对称的美,利用中心对称,可以探索并证明图形的性质.请思考在下列图形中,是中心对称图形但不一定是轴对称图形的为( )
A.扇形 B.平行四边形 C.等边三角形 D.矩形
【答案】B
【解答】解:A.扇形是轴对称图形,不是中心对称图形,故此选项不合题意;
B.平行四边形不一定是轴对称图形,是中心对称图形,故此选项符合题意;
C.等边三角形是轴对称图形,不是中心对称图形,故此选项不合题意;
D.矩形既是轴对称图形,又是中心对称图形,故此选项不合题意;
故选:B.
八.正方形的性质(共1小题)
9.(2022•泰州)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为( )
A. B.2 C.2 D.4
【答案】C
【解答】解:如图,连接AE,
∵四边形DEFG是正方形,
∴∠EDG=90°,EF=DE=DG,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADE=∠CDG,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴d1+d2+d3=EF+CF+AE,
∴点A,E,F,C在同一条线上时,EF+CF+AE最小,即d1+d2+d3最小,
连接AC,
∴d1+d2+d3最小值为AC,
在Rt△ABC中,AC=AB=2,
∴d1+d2+d3最小=AC=2,
故选:C.
九.切线的性质(共2小题)
10.(2022•镇江)如图,在等腰△ABC中,∠BAC=120°,BC=6,⊙O同时与边BA的延长线、射线AC相切,⊙O的半径为3.将△ABC绕点A按顺时针方向旋转α(0°<α≤360°),B、C的对应点分别为B′、C′,在旋转的过程中边B′C′所在直线与⊙O相切的次数为( )
A.1 B.2 C.3 D.4
【答案】C
【解答】解:如图1,由题意可知⊙O同时与边BA的延长线、射线AC相切,⊙O的半径为3,
设⊙O与边BA的延长线、射线AC分别相切于点T、点G,连接OA交⊙O于点L,连接OT,
∴AT⊥OT,OT=3,
作AE⊥BC于点E,OH⊥BC于点H,则∠AEB=90°,
∵AB=AC,∠BAC=120°,BC=6,
∴BE=CE=BC=3,∠B=∠ACB=(∠180﹣∠BAC)=30°,
∴AE=BE•tan30°=3×=3,
∵∠TAC=180°﹣∠BAC=60°,
∴∠OAG=∠OAT=∠TAC=30°,
∴∠OAG=∠ACB,
∴OA∥BC,
∴OH=AE=OT=OL=3,
∴直线BC与⊙O相切,
∵∠ATO=90°,
∴OA=2OT=6,
∴AL=3,
作AK⊥B′C′于点K,由旋转得AK=AE=3,∠AKB′=∠AEB=90°,
如图2,△ABC绕点A旋转到点K与点L重合,
∵∠OLB′=180°﹣∠ALB′=180°﹣∠AKB′=90°,
∴B′C′⊥OL,
∵OL为⊙O的半径,
∴B′C′与⊙O相切;
如图3,△ABC绕点A旋转到B′C′∥OA,作OR⊥B′C′交C′B′的延长线于点R,
∵OR=AK=3,
∴B′C′与⊙O相切;
当△ABC绕点A旋转到B′C′与BC重合,即旋转角α=360°,则B′C′与⊙O相切,
综上所述,在旋转的过程中边B′C′所在直线与⊙O相切3次,
故选:C.
11.(2022•无锡)如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是( )
A.AE⊥DE B.AE∥OD C.DE=OD D.∠BOD=50°
【答案】C
【解答】解:∵弦AD平分∠BAC,∠EAD=25°,
∴∠OAD=∠ODA=25°.
∴∠BOD=2∠OAD=50°.
故选项D不符合题意;
∵∠OAD=∠CAD,
∴∠CAD=∠ODA,
∴OD∥AC,即AE∥OD,故选项B不符合题意;
∵DE是⊙O的切线,
∴OD⊥DE.
∴DE⊥AE.故选项A不符合题意;
如图,过点O作OF⊥AC于F,则四边形OFED是矩形,
∴OF=DE.
在直角△AFO中,OA>OF.
∵OD=OA,
∴DE<OD.
故选项C符合题意.
故选:C.
一十.扇形面积的计算(共1小题)
12.(2022•连云港)如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A.π﹣ B.π﹣ C.π﹣2 D.π﹣
【答案】B
【解答】解:连接OA、OB,过点O作OC⊥AB,
由题意可知:∠AOB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∴AB=AO=BO=2
∴S扇形AOB==π,
∵OC⊥AB,
∴∠OCA=90°,AC=1,
∴OC=,
∴S△AOB==,
∴阴影部分的面积为:π﹣;
故选:B.
一十一.圆锥的计算(共1小题)
13.(2022•无锡)在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )
A.12π B.15π C.20π D.24π
【答案】C
【解答】解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB===5,
由已知得,母线长l=5,半径r为4,
∴圆锥的侧面积是S=πlr=5×4×π=20π.
故选:C.
一十二.相似三角形的性质(共1小题)
14.(2022•连云港)△ABC的三边长分别为2,3,4,另有一个与它相似的三角形DEF,其最长边为12,则△DEF的周长是( )
A.54 B.36 C.27 D.21
【答案】C
【解答】解:方法一:设2对应的边是x,3对应的边是y,
∵△ABC∽△DEF,
∴==,
∴x=6,y=9,
∴△DEF的周长是27;
方式二:∵△ABC∽△DEF,
∴=,
∴=,
∴C△DEF=27;
故选:C.
一十三.相似三角形的判定(共1小题)
15.(2022•连云港)如图,将矩形ABCD沿着GE、EC、GF翻折,使得点A、B、D恰好都落在点O处,且点G、O、C在同一条直线上,同时点E、O、F在另一条直线上.小炜同学得出以下结论:①GF∥EC;②AB=AD;③GE=DF;④OC=2OF;⑤△COF∽△CEG.其中正确的是( )
A.①②③ B.①③④ C.①④⑤ D.②③④
【答案】B
【解答】解:由折叠性质可得:DG=OG=AG,AE=OE=BE,OC=BC,
∠DGF=∠FGO,∠AGE=∠OGE,∠AEG=∠OEG,∠OEC=∠BEC,
∴∠FGE=∠FGO+∠OGE=90°,∠GEC=∠OEG+∠OEC=90°,
∴∠FGE+∠GEC=180°,
∴GF∥CE,故①正确;
设AD=2a,AB=2b,则DG=OG=AG=a,AE=OE=BE=b,
∴CG=OG+OC=3a,
在Rt△CGE中,CG2=GE2+CE2,
(3a)2=a2+b2+b2+(2a)2,
解得:b=a,
∴AB=AD,故②错误;
在Rt△COF中,设OF=DF=x,则CF=2b﹣x=2a﹣x,
∴x2+(2a)2=(2a﹣x)2,
解得:x=a,
∴DF=×a=a,2OF=2×a=2a,
在Rt△AGE中,GE==a,
∴GE=DF,OC=2OF,故③④正确;
无法证明∠FCO=∠GCE,
∴无法判断△COF∽△CEG,故⑤错误;
综上,正确的是①③④,
故选:B.
一十四.方差(共1小题)
16.(2022•镇江)第1组数据为:0、0、0、1、1、1,第2组数据为:、,其中m、n是正整数下列结论:①当m=n时,两组数据的平均数相等;②当m>n时,第1组数据的平均数小于第2组数据的平均数;③当m<n时,第1组数据的中位数小于第2组数据的中位数;④当m=n时,第2组数据的方差小于第1组数据的方差.其中正确的是( )
A.①② B.①③ C.①④ D.③④
【答案】B
【解答】解:①第1组平均数为:0.5;
当m=n时,第2组平均数为:==0.5;
∴①正确;
②当m>n时,m+n>2n,<0.5;
∴第1组数据的平均数大于第2组数据的平均数;
∴②错误;
③第1组数据的中位数=0.5;
当m<n时,若m+n为奇数,第2组数据的中位数是1,若m+n为偶数,第2组数据的中位数是1,
∴当m<n时,第2组数据的中位数是1,
∴m<n时,第1组数据的中位数小于第2组数据的中位数;
∴③正确;
④第1组数据的方差:=0.25;
第2组数据的方差:=0.25;
∴当m=n时,第2组数据的方差等于第1组数据的方差;
∴④错误;
故答案为:B.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2023/6/10 15:42:43;用户:15194141305;邮箱:15194141305;学号:44628700
江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-04填空题提升题: 这是一份江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-04填空题提升题,共36页。
江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-02选择题基础题②: 这是一份江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-02选择题基础题②,共19页。
江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-02选择题基础题①: 这是一份江苏省2022年各地区中考数学真题按题型难易度分层分类汇编(14套)-02选择题基础题①,共20页。












