四川省达州市渠县中学2022-2023学年七年级下学期期末数学练习题（一）

四川省达州市渠县中学2022-2023学年七年级下学期期末数学练习题（一）

一、选择题

1.已知a=3100，b=475，c=750，则a，b，c的大小关系为（    ）
A.a>b>c        B.a>c>b       C.c>a>b         D.b>c>a
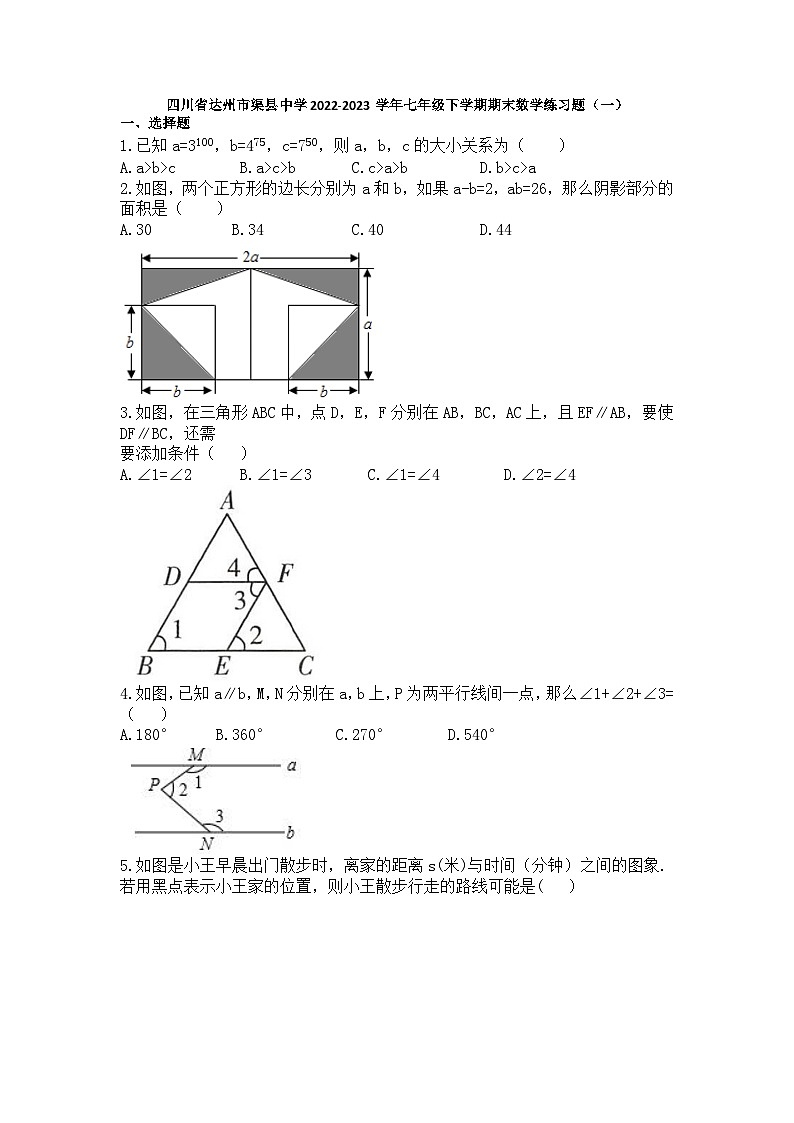
2.如图，两个正方形的边长分别为a和b，如果a-b=2，ab=26，那么阴影部分的面积是（    ）
A.30          B.34           C.40            D.44
 

3.如图，在三角形ABC中，点D，E，F分别在AB，BC，AC上，且EF∥AB，要使DF∥BC，还需
要添加条件（   ）
A.∠1=∠2      B.∠1=∠3       C.∠1=∠4        D.∠2=∠4
 

4.如图，已知a∥b，M，N分别在a，b上，P为两平行线间一点，那么∠1+∠2+∠3=（   ）
A.180°     B.360°        C.270°       D.540°
 

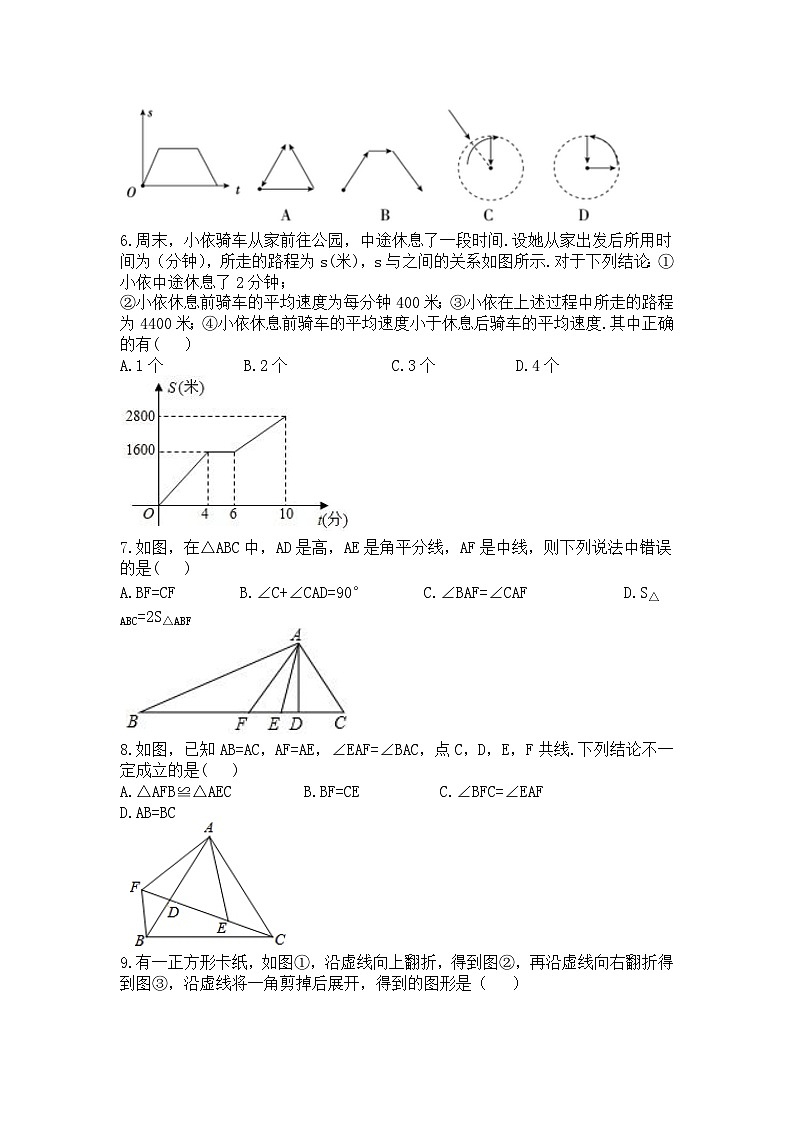
5.如图是小王早晨出门散步时，离家的距离s(米)与时间（分钟）之间的图象.若用黑点表示小王家的位置，则小王散步行走的路线可能是(   ）

6.周末，小依骑车从家前往公园，中途休息了一段时间.设她从家出发后所用时间为（分钟），所走的路程为s(米)，s与之间的关系如图所示.对于下列结论：①小依中途休息了2分钟；
②小依休息前骑车的平均速度为每分钟400米；③小依在上述过程中所走的路程为4400米；④小依休息前骑车的平均速度小于休息后骑车的平均速度.其中正确的有(   ）
A.1个          B.2个             C.3个          D.4个

7.如图，在△ABC中，AD是高，AE是角平分线，AF是中线，则下列说法中错误的是(   )
A.BF=CF        B.∠C+∠CAD=90°       C.∠BAF=∠CAF            D.S△ABC=2S△ABF
 

8.如图，已知AB=AC，AF=AE，∠EAF=∠BAC，点C，D，E，F共线.下列结论不一定成立的是(   )
A.△AFB≌△AEC         B.BF=CE          C.∠BFC=∠EAF            D.AB=BC
 

9.有一正方形卡纸，如图①，沿虚线向上翻折，得到图②，再沿虚线向右翻折得到图③，沿虚线将一角剪掉后展开，得到的图形是（   ）
 

10.如图，在钝角三角形ABC中，∠ABC=30°且AB＞AC.(1)以点C为圆心，CA长为半径画弧；(2)以点B为圆心，BA长为半径画弧，交前弧于点E;(3)连接AE交BC的延长线于点D.下列结论：①BD垂直平分AB；②AC平分∠BAD；③S△ABC=BC.AD，④△ABC与△EBC成轴对称.其中一定成立的是（   ）
A.①②③     B.②③④     C.①③④    D.①②③④
 

11.如图①，在平整的地面上有一个不规则的图案（图中阴影部分），小颖想知道该图案的面积是多少，她采取了以下的方案：先用一个长为8m，宽为5m的长方形框架（框架厚度忽略不计)把这个图案围起来，然后在适当的位置随机地朝长方形区域扔小球，并记录小球落在不规则图案的次数（球扔在长方形边上或长方形区域外不计试验结果），她将若干次有效试验的结果绘制成了图②，由此她估计不规则图案的面积为（   ）
A.12m2         B.13m2              C.14m2           D.15m2
 

12.如图，在4×4正方形网格中，已有4个小正方形被涂黑，现任意选取一个白色的小正方形并涂黑，使整个黑色部分构成一个轴对称图形的概率是（   ）
A.             B.               C.              D.
 

13.某同学粗心大意，计算多项式乘法时，把等式(x2+2x+4)(x-▲)=x-■中的两个常数弄污了，则式子中的■，▲对应的一组数可以是（   ）
A.20,5          B.16,4             C.13,3             D.8,2
14.如图，已知AB⊥MN，CD⊥MN，垂足分别为点B和D，BE和DF分别平分∠ABN和∠CDN，有下列结论：①AB∥CD;②∠1=∠2;③CD⊥EF;④∠E+∠F=180°.其中结论正确的是（   ）
A.①②③     B.②③④         C.①②④            D.③④
 

15.如图，折叠直角三角形纸片ABC，使得点A，B都与斜边AB上的点F重合，折痕分别为DE和GH，则下列结论不一定成立的是(  )
A.DH=AB    B.EF=FG     C.EF⊥FG    D.DE∥GH
 

16.如图，在△ABC中，AB=AC，BE=CD，BD=CF，则∠EDF的度数为(  )
A.45°-∠A      B.90°-∠A          C.90°-∠A      D.180°-∠A
 

17.如图，已知∠FED+∠BGF=180°，∠B=∠D，若∠AED=45°，∠BEF=35°，则∠BCF的度数为(   )
A.55°      B.50°       C.45°       D.35°
 

18.如图，AD是△ABC的角平分线，CE⊥AD，垂足为F.若∠CAB=40°，∠B=50°，则∠CDE的度数为(   )
A.135°      B.140°     C.145°      D.150°
 

19.已知(x-2021)2+(x-2023)2=34，则(x-2022)2的值是（   ）
A.4           B.8             C.12             D.16
20.如图，点B，C，E在同一条直线上，△ABC与△CDE为等腰三角形，CA=CB，CD=CE，∠ACB=∠DCE，∠BGC=∠AFC.下列结论错误的是（   ）
A.DG=EF          B.CG=CF          C.AE=BD           D.AC+CD=AE
 

二、填空题

21.小亮在计算(5m+2n)(5m-2n)+(3m+2n)2-3m(11m+4n)的值时，把n的值看错了，其结果等于25，细心的小敏把正确的n的值代人计算，其结果也是25.为了探究明白，她又把=2022代入，结果还是25，则m的值为_______.
22.如图，在长方形ABCD中放人一个边长为8的大正方形ALMN和两个边长为6的小正方形（正方形DEFG和正方形HIJK).三个阴影部分的面积满足2S3+S1-S2=2，则长方形ABCD的面积为_______.
 

23.如图，BC∥0A，∠B=∠A=100°，点E，F在BC上，OE平分∠B0F，且∠F0C=∠A0C，有下列结论：①0B∥AC;②∠E0C=45°;③∠0CB:∠0FB=1:3;④若∠0EB=∠0CA，则∠0CA=60°.其中正确的是_______.(填序号)
 

24.有两条笔直且平行的景观道AB，CD上放置P，Q两盏激光灯（如图所示），若光线PB按顺时针方向以每秒6°的速度旋转至PA便立即回转，并不断往返旋转；光线QC按顺时针方向以每秒2°的速度旋转至QD边就停止旋转（同时光线PB也停止旋转）.若光线QC先转5秒，光线PB才开始转动，当光线PB旋转时间为_______秒时，PB1∥QC1.
 

25.小亮从家骑车上学，先经过一段平路到达A地后，再上坡到达B地，最后下坡到达学校,所行驶路程s(千米)与时间（分钟）的关系如图所示.如果返回时，上坡、下坡、平路的速度仍然保持不变，那么他从学校回到家需要的时间是_______分钟.

26.甲、乙两车分别从A，B两地同时相向匀速行驶.当乙车到达A地后，继续保持原速向远离B的方向行驶，而甲车到达B地后立即掉头，并保持原速与乙车同向行驶，经过一段时间后两车同时到达C地.设两车行驶的时间为x(h)，两车之间的距离为y(km)，y与x之间的关系如图所示，当甲车到达B地时，乙车距离A地_______km.

27.程老师制作了如图①所示的学具，用来探究“边边角条件是否可确定三角形的形状”问题.操作学具时，点Q在轨道槽AM上运动，点P既能在以点A为圆心，8为半径的半圆轨道槽上运动，也能在轨道槽QN上运动.图②是操作学具时，所对应某个位置的图形示意图，有以下结论：①当∠PAQ=30°，PQ=6时，可得到形状唯一确定的△PAQ;②当∠PAQ=30°，PQ=9时，可得到形状唯一确定的△PAQ;③当∠PAQ=90°，PQ=10时，可得到形状唯一确定的△PAQ;④当∠PAQ=150°，PQ=12时，可得到形状唯一确定的△PAQ.其中正确的是___________.(填序号)

28.如图，∠A=∠B=90°，AB=60，E，F分别为线段AB和射线BD上的一点，若点E从点B出发向点A运动，同时点F从点B出发向点D运动，二者速度之比为3：7，运动到某时刻同时停止，在射线AC上取一点G，要使△AEG与△BEF全等，则AG的长为______.

29.如图，在五边形ABCDE中，∠BAE=136°，∠B=∠E=90°，在BC，DE上分别找一点M，N使得△AMWN的周长最小时，则∠AMN+∠ANM的度数为_____.
 

30.已知锐角∠A0B，如图，(1)在射线0A上取一点C，以点0为圆心，OC长为半径作弧，交射线OB于点D，连接CD;(2)分别以点C，D为圆心、CD长为半径作弧，两弧交于点P，连接CP，DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形，有下列结论：①CD⊥OP;②CP=2QC;③∠AOP=∠BOP;④CP∥OB.其中一定成立的是______.(填序号)
 

31.如图，D，E，F，G分别是BC，AD，BE，CE的中点，若△ABC内有一点M，则点M落在△AFG内（含边界）的概率为________.
 

32.斐波那契螺旋线，也称“黄金螺旋线”，是根据斐波那契数列1，1，2，3，5，画出来的螺旋曲线.如图，白色小圆是边长为1的正方形内最大的圆，黑色曲线就是斐波那契螺旋线，它是依次在以1，2，3，5为边长的正方形中画一个圆心角为90°的扇形，将其圆弧连接起来得到的.若在长方形ABCD内随机取一点，则此点取自阴影部分的概率是________.
 

33.如图，长方形ABCD的周长为12，面积为3，分别以BC，CD为边作正方形，则图中阴影部分的面积为_______.
 

34.已知MN∥PQ，将一副直角三角尺ABC和ADE按照如图方式摆放在平行线之间，且边BC落在直线MN上，边DE落在直线PQ上，其中∠ACB=60°，∠AED=45°.若C0平分∠ACB，E0平分∠AED，两条角平分线相交于点O，则∠COE的度数是_______.

35.如图，在△ABC中，AD为BC边上的中线，将△ABD沿AD翻折得到△AB′D，AB交BC于点H，连接B′C，若S△B′CH=2，CH:DH=1:2，则△ABC的面积是________.
 

36.如图，点C在线段BD上，AB⊥BD于点B，ED⊥BD于点D，∠ACE=90°，且AC=5cm，CE=6cm，点P以2cm/s的速度沿A→C→E向终点E运动，同时点Q以3cm/s的速度从E开始，在线段EC上往返运动（即沿E一C一→E→C→…运动），当点P到达终点时，P，Q同时停止运动,过P，Q分别作BD的垂线，垂足为M，N.设运动时间为ts，当以P，C，M为顶点的三角形与△QCN全等时，t的值为________.

37.如图，AE∥CF，∠ACF的平分线交AE于点B，G是CF上的一点，∠GBE的平分线交CF于点D，且BD⊥BC.有下列结论：①BC平分∠ABG;②AC∥BG;③与∠DBE互余的角有2个；④若∠A=ɑ，则∠BDF=180°-,其中正确的是_______.(填序号)
 

38.如图，在△ABC中，∠ACB=90°，AC=7cm，BC=3cm，CD为AB边上的高，点E从点B出发，在直线BC上以2cm/s的速度移动，过点E作BC的垂线交直线CD于点F，当点E运动
_______s时，CF=AB.
 

39.如图，在△ABC中，∠A=22°，D为AB边的中点，E为AC边上一点，将△ADE沿着DE翻折，得到△A′DE，连接A′B.当A′B=A′D时，∠A′EC的度数为______.
 

40.如图，在Rt△ABC中，∠ABC=90°，以AC为边，作△ACD，满足AD=AC，E为BC上一点,连接AE，2∠BAE=∠CAD，连接DE.下列结论：①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB，则AE⊥AD;④DE=CE+2BE.其中一定成立的是______.(填序号)
 

三、解答题

41.如图，把一个木制正方体的表面涂上颜色，然后将正方体分割成64个大小相同的小正方体，从这些小正方体中任意取出一个，求取出的小正方体：
(1)三面涂有颜色的概率；(2)两面涂有颜色的概率；
 

42.已知△ABC，AB=AC，D为直线CB上一点，E为直线CA上一点，AD=AE，设∠BAD=α，∠CDE=β.
(1)如图，若点D在线段BC上，点E在线段AC上，∠B=60°，∠ADE=70°，那么α，β之间的关系式是_____.
(2)是否存在不同于(1)中的α，β之间的关系式？若存在，求出这个关系式；若不存在，请说明理由.

43.在△ABC中，D，E是BC边上的两点，且BA=BD，CA=CE，连接AD，AE.
(1)如图①，若∠B=40°，∠C=60°，求∠DAE的度数；
(2)如图②，若∠BAC=ɑ(0°＜ɑ＜180°)，试说明：∠DAE=90°-ɑ；
(3)若∠DAE=45°，则∠BAC=______°.

44.阅读：若x满足(60-x)(x-40)=30，求(60-x)2+(x-40)2的值.

解：设(60-x)=a，(x-40)=b，则(60-x)(x-40)=ab=_________,a+b=(60-x)+(x-40)=______，所以(60-x)2+(x-40)2=a2+b2=(a+b)2-2ab=__________.
请仿照上例解决下面的问题：
(1)补全题目中横线处；
(2)已知(30-x)(x-20)=-10，求(30-x)2+(x-20)2的值；
(3)若x满足(2023-x)2+(2022-x)2=2021，求(2023-x)(x-2022)的值；
(4)如图，正方形ABCD的边长为x，AE=10，CG=25，长方形EFGD的面积是400，四边形
NGDH和MEDQ都是正方形，PQDH是长方形，求图中阴影部分的面积（结果必须是一个具体
数值).

45.如图①，AB∥CD，∠PAB=125°，∠PCD=115°，求∠APC的度数.
小明的思路是：过点P作PM∥AB，通过平行线的性质来求∠APC.
(1)按小明的思路，易求得∠APC的度数为_______.
(2)如图②，AB∥CD，点P在直线a上运动，记∠PAB=α，∠PCD=β，当点P在B，D两
点之间运动时，问∠APC与α，β之间有何数量关系？请说明理由；
(3)在(2)的条件下，如果点P在B，D两点外侧运动时（点P与B，D两，点不重合），请直接写出∠APC与α，β之间的数量关系.

46.如图①是一个大长方形减去一个小长方形后形成的图形，已知动点P以1cm/s的速度沿边框A→B→C→D→E→F的路径移动，相应的三角形AFP的面积S(cm2)与时间x(s)之间的关系如图②所示，若AF=3cm，请求出：
(1)图①中的BC的长是多少？
(2)图②中的a是多少？
(3)图①中的图形面积是多少？
(4)图②中的b是多少？
 

47.(1)问题背景：如图①，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°，探究图中线段BE，EF，FD之间的数量关系.
小王同学探究此问题的方法是：延长FD至点G，使DG=BE，连接AG，先说明△ABE≌△ADG，再说明△AEF≌△ACF，即可得到BE，EF，FD之间的数量关系是_______________.
(2)拓展应用：如图②，在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD
上的点，且∠EAF=∠BAD，上述结论是否仍然成立？请说明理由.
(3)实际应用：如图③，在某次军事演习中，舰艇甲在指挥中心(0处)北偏西30°的A处，舰艇乙在指挥中心南偏东70的B处，并且两舰艇到指挥中心的距离相等.接到行动指令后，舰艇甲向正东方向以60海里时的速度前进，舰艇乙沿北偏东50°的方向以80海里时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离.
 

48.已知，如图①，∠A=50°，点C为射线AD上一点（不与点A重合），连接BC.
问题提出：
(1)如图②，AB∥CE，∠BCD=73°，则∠B的度数为______.
类比探究：
(2)在图①中，探究∠A，∠B和∠BCD之间有怎样的数量关系，并用平行线的性质说明理由；
拓展延伸：
(3)如图③，在射线BC上取一点O，过O点作直线MN使MN∥AD，BE平分∠ABC交AD于E点，OF平分∠BON交AD于F点，OG∥BE交AD于G点，当C点沿着射线AD方向运动时，∠FOG的度数是否会变化？若变化，请说明理由；若不变，请求出这个不变的值.
 

49.问题背景：课外兴趣小组活动时，老师提出了如下问题：如图①，在△ABC中，若AB=4，AC=3，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE=AD，连接BE，则得到△ADC≌△EDB，他用到的判定定理是：_____________;(用字母表示)
问题解决：小明发现，解题时条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求解的结论集合到同一个三角形中，请写出小明解决问题的完整过程；
拓展应用：如图②，以△ABC的边AB，AC为边向外作△ABE和△ACD，AB=AE，AC=AD，∠BAE=∠CAD=90°，M是BC的中点，连接AM，DE.当AM=3时，求DE的长.

50.如图①，△ABC为等腰直角三角形，AB=AC，△ADE为等腰直角三角形，AD=AE，点D在直线BC上，连接CE.
(1)判断：CE，CD，BC之间的数量关系，CE与BC所在直线之间的位置关系，并说明理由：
(2)若D在CB的延长线上（如图②）,(1)中的结论是否成立？若成立，请直接写出结论,若不成立，请什么理由.

(3)若D在BC的延长线上（如图③），(1)中的结论是否成立？若成立，请直接写出结论，若不成立，请写出你发现的结论，并计算：当CE=10cm，CD=2cm时，BC的长.