专题06　圆周运动-冲刺高考物理大题突破+限时集训（全国通用）

专题06　圆周运动

  【例题】（2023春·天津·高三校联考开学考试）如图所示为一游艺系统示意图。光滑半圆轨道竖直固定，直径沿竖直方向，半径为，A点有一质量为的小物块处于静止状态。光滑足够长的水平平台上有一平板小车，质量为，其左端恰好与半圆轨道的B点平齐，恰能使小物块离开B点后滑上小车。在A点给物块一个水平向左的瞬时冲量I，物块以的速度滑上小车，恰停在小车右端。已知物块与小车之间的动摩擦因数为。求

（1）在B点物块对轨道压力大小；

（2）瞬时冲量I的大小；

（3）小车的长度。

【答案】  （1）10N；（2）；（3）1m

【解析】（1）滑块在B点时，由牛顿第二定律

解得

FN=10N

根据牛顿第三定律可知在B点物块对轨道压力大小

F′N=10N

（2）从A到B，由机械能守恒定律

其中

I=mv0

解得

（3）物块滑上小车时，由动量守恒定律和能量关系

解得

L=1m

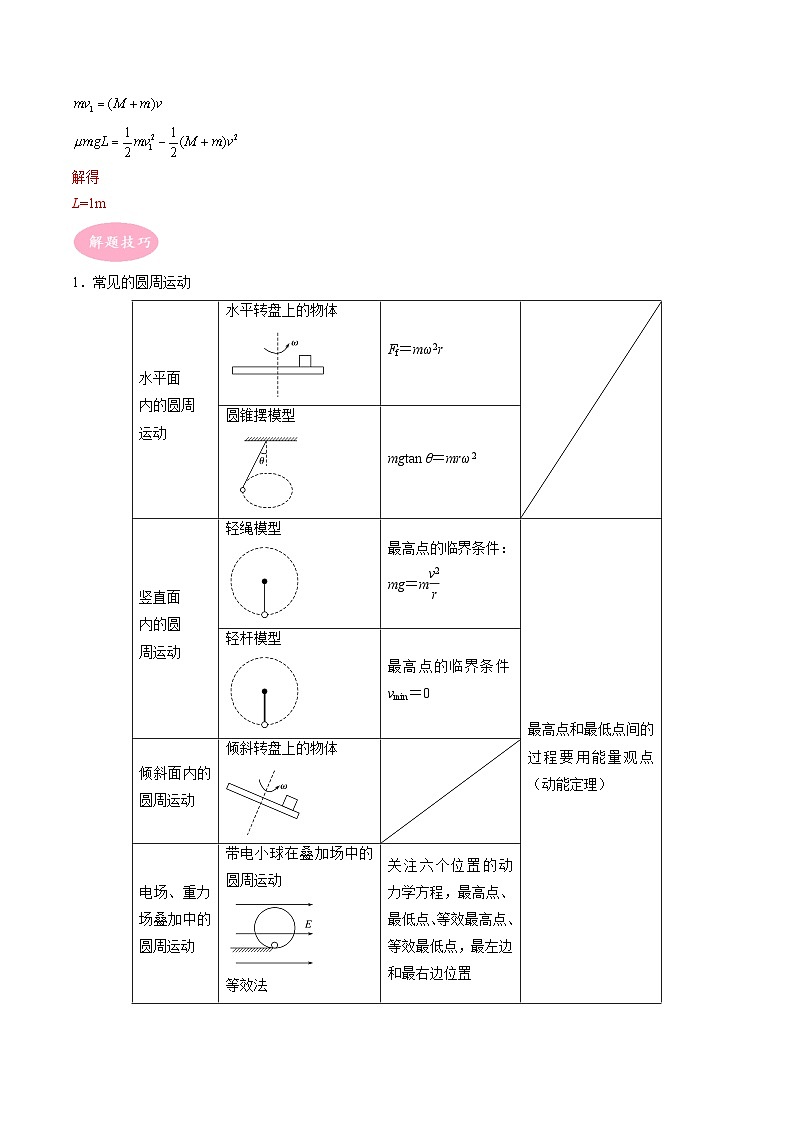
1．常见的圆周运动

2．圆周运动的三种临界情况

（1）接触面滑动临界：摩擦力达到最大值．

（2）接触面分离临界：FN＝0.

（3）绳恰好绷紧：FT＝0；绳恰好断裂：FT达到绳子最大承受拉力．

（4）竖直面内的圆周运动两种模型

①绳球模型：小球能通过最高点的条件是v≥。

②杆球模型：小球能到达最高点的条件是v≥0。

【变式训练】（2023·山东济宁·济宁市育才中学统考一模）火星的半径是地球半径的二分之一，质量为地球质量的十分之一，忽略星球自转影响，地球表面重力加速度g=10m/s²。假定航天员在火星表面利用如图所示的装置研究小球的运动。竖直平面放置的光滑半圆形管道固定在水平面上，一直径略小于管道内径的小球（可视为质点）沿水平面从管道最低点A进入管道，从最高点B脱离管道后做平抛运动，1s后与倾角为37°的斜面垂直相碰于C点。已知半圆形管道的半径为r=3m，小球的质量为m=0.5kg，sin37°=0.6，cos37°=0.8。求：

（1）火星表面的重力加速度的大小；

（2）C与B点的水平距离；

（3）小球经过管道的A点时，对管壁的压力的大小。

【答案】  （1）；（2）；（3）11.5N

【解析】（1）根据“黄金代换式”，对地球

对火星

火星的半径是地球半径的二分之一，质量为地球质量的十分之一，得火星表面的重力加速度的大小为

（2）小球从B点到C点做平抛运动，则

小球与斜面垂直相碰于C点，则

C与B点的水平距离为

（3）由（1）可得小球在B点的速度为

小球由A点到B点，根据机械能守恒

根据牛顿第二定律

得

根据牛顿第三定律，则小球经过管道的A点时，对管壁的压力的大小为11.5N。

1．（2023·山东滨州·高三统考期末）如图，质量为的小物块，用长的细线悬挂于点，现将细线拉直并与水平方向夹角，由静止释放，小物块下摆至最低点处时，细线达到其最大承受力并瞬间断开，小物块恰好从水平传送带最左端点滑上传送带，传送带以的速度逆时针匀速运转，其上表面距地面高度，小物块最后从传送带左端飞出，并恰好从光滑斜面顶端沿斜方面滑上斜面。斜面高，倾角，斜面底端挡板上固定一轻弹簧。小物块沿斜面下滑一段距离后，压缩弹簧，小物块沿斜面运动的最大距离，取。求：

（1）绳子能承受的最大拉力的大小；

（2）传送带速度大小满足的条件；

（3）弹簧的最大弹性势能。

【答案】  （1）：（2）；（3）

【解析】（1）小球从静止摆到最低点过程中，根据机械能守恒定律有

解得

小球在点时，根据向心力公式有

联立解得

根据牛顿第三定律，刚到最低点细线达到其最大承受力。

（2）由于小物块恰好沿斜面方向落到光滑斜面上，即小物块落到斜面顶端时速度方向沿斜面方向，则

联立以上各式得

则传送带速度大于等于。

（3）小物块在斜面顶端速度

小物块从顶端到压缩弹簧最短，由机械能守恒，弹簧最大的弹性势能为

解得

2．（2023·安徽淮北·统考一模）2022年2月我国成功举办了第24届“冬奥会”，冬奥会让冰雪运动走向大众，让更多人认识冰雪，爱上冰雪，北京冬奥留下的不只是场馆设施等物质遗产，还有影响深远的文化和精神遗产。如图甲所示为2022年北京冬奥会首钢滑雪大跳台，将其简化为如图乙所示模型：段和段是长度均为的倾斜滑道，倾角均为；段是半径的一段圆弧轨道，圆心角为，与段平滑连接；段为结束区。一滑雪爱好者连同装备总质量，从A点由静止出发沿着滑道下滑，从C点水平抛出落到斜面上的点，点到的距离。该爱好者可看作质点，将到的运动简化为平抛运动处理。忽略其运动过程中所受的空气阻力，，重力加速度取。求：

（1）该人运动到点时对滑道的压力大小；

（2）从开始运动到落至点的过程中摩擦阻力做的功。

【答案】  （1）；（2）

【解析】（1）从处平抛，竖直方向有

水平方向有

得

在处，据牛顿第二定律有

解得滑道对人的支持力为

据牛顿第三定律，人运动到点时对滑道的压力与大小相等，为。

（2）从到由动能定理得

解得

3．（2023春·山西·高三校联考开学考试）某课外小组制作了如图所示的轨道，数字“0”和“9”竖直轨道内部光滑且固定，水平直轨道粗糙，左侧固定水平弹射器，整个装置位于同一竖直平面。两小球可视为质点，小球1压缩弹射器并被锁定，小球2位于轨道“9”最底端处，质量均为，与水平轨道之间的动摩擦因数均为，小球接触即粘合在一起。轨道小圆弧半径，大圆弧半径为。圆弧轨道最低点与相靠但不相叠，小球能够无能量损失地通过。当弹射器释放的弹性势能为时，小球恰好能经过点。不计空气阻力，重力加速度取。

（1）求弹射器的弹性势能；

（2）弹射器释放的弹性势能为时，求两球碰后瞬间对圆弧轨道点压力大小；

（3）弹射器释放的弹性势能为时，两球碰后能经过点抛出，（假设抛出后与轨道没有碰撞），判断抛出后运动的最高点与点相比哪点高。

【答案】  （1）0.22J；（2）0.45N；（3）D点高

【解析】（1）小球1离开弹射器后到达点，根据功能关系可得

恰好能经过点，重力刚好提供向心力，则有

联立解得

（2）弹射器释放的弹性势能为时，碰前第小球1到达点瞬时速度为，根据功能关系可得

解得

两小球发生非弹性碰撞，设碰后瞬间速度为，根据动量守恒可得

解得

重力和支持力的合力提供向心力，则有

根据牛顿第三定律，碰后瞬间对圆弧轨道点压力大小为

联立解得

（3）设两小球经过点时速度大小为，由到，根据机械能守恒得

解得

到，根据机械能守恒得

在点水平方向速度分量为

联立解得

由于最高点的速度大于点速度，根据机械能守恒可知，抛出后运动的最高点与点相比，点高。

4．（2023·辽宁丹东·高三统考期末）如图甲所示，光滑半圆形曲面固定在水平地面上，其直径AB水平，曲面体内有压力传感器，可测出各时刻物体对曲面体内表面压力的大小。某时刻一小球从曲面最左端A点的正上方某处自由下落，它对曲面体内表面的压力大小随时间t的变化的规律如图乙所示，结合图像求：（不计空气阻力，重力加速度）

（1）小球刚接触曲面时的速度的大小；

（2）小球的质量m；

（3）在0.9s~1.2s内，曲面体对小球的支持力产生的冲量。

【答案】  （1）；（2）0.7kg；（3），方向竖直向上

【解析】（1）0.3s－0.9s小球做竖直上抛运动，t＝0.6s

则小球刚接触曲面时的速度

（2）在A点

最低点C

A到C由动能定理

可得

m＝0.7kg

（3）0.9s－1.2s是从B回到A的过程，以向上为正，对小球由动量定理

方向竖直向上。

5．（2023·新疆乌鲁木齐·统考一模）如图所示，一半径为R的光滑圆轨道固定在竖直平面内，两小球A、B从与圆心O等高处同时由静止开始释放，释放后两小球沿圆轨道运动。两小球第一次发生弹性正碰后，小球A静止，小球B继续沿圆轨道运动。已知小球B的质量为m，重力加速度大小为g，小球A、B可视为质点且碰撞时间极短。求：

（1）两小球第一次发生弹性碰撞后的瞬间，小球B的速度v的大小；

（2）小球B第一次通过圆轨道最高点时，轨道对小球B的作用力F的大小。

【答案】  （1）；（2）3mg

【解析】（1）设小球A、B第一次运动到轨道最低点时的速度大小为，小球的质量为，根据机械能守恒定律和动量守恒定律可得

解得

（2）设小球第一次通过圆轨道最高点的速度大小为，根据机械能守恒定律和牛顿第二定律得

解得

6．（2023·浙江·模拟预测）如图为某游戏装置的示意图。AB、CD均为四分之一圆弧，E为圆弧DEG的最高点，各圆弧轨道与直轨道相接处均相切。GH与水平夹角为θ＝37°，底端H有一弹簧，A、O₁、O₂、D、O₃、H在同一水平直线上。一质量为0.01kg的小钢球（其直径稍小于圆管内径，可视作质点）从距A点高为h处的O点静止释放，从A点沿切线进入轨道，B处有一装置，小钢球向右能无能量损失的通过，向左则不能通过且小钢球被吸在B点。若小钢球能够运动到H点，则被等速反弹。各圆轨道半径均为R＝0.6m，BC长L＝2m，水平直轨道BC和GH的动摩擦因数μ＝0.5，其余轨道均光滑，小钢球通过各圆弧轨道与直轨道相接处均无能量损失。某次游戏时，小钢球从O点出发恰能第一次通过圆弧的最高点E。（sin37°＝0.6，cos37°＝0.8，g＝10m/s2）求：

（1）小钢球第一次经过C点时的速度大小vC；

（2）小钢球第一次经过圆弧轨道最低点B时对轨道的压力大小FB（保留两位小数）；

（3）若改变小钢球的释放高度h，求出小钢球在斜面轨道上运动的总路程s与h的函数关系。

【答案】  （1）；（2）；（3）见解析

【解析】（1）小钢球从O点出发恰能第一次通过圆弧的最高点E，则小球到E点的速度为0，小球从C点到E点，根据动能定理得

代入数据解得

（2）从B点到C点，由动能定理得

小钢球经过B点，由牛顿第二定律得

代入数据联立解得

根据牛顿第三定律得，小钢球对轨道的压力大小

FB＝N＝0.83N

（3）若小钢球恰能第一次通过E点，设小钢球释放点距A点为h1，从释放到E点，由动能定理得

代入数据解得

h1＝1.6m

若小钢球恰能第二次通过E点，设小球钢释放点距A点为h2，从释放到E点，由动能定理得

代入数据解得

h2＝2.24m

①若小球释放高度h＜1.6m，无法到达E点，s＝0

②若小球释放高度1.6m≤h＜2.24m，小球能经过E点一次，因为μ＜tanθ，则小钢球最终停在H点，从释放点到停在H点，根据动能定理得

代入数据解得

s＝2.5（h﹣1）

③若小球释放高度2.24m≤h，小球经过E点两次

7．（2023·山东枣庄·高三统考期末）如图甲所示，一水平放置的内表面光滑对称“V”型二面体，可绕其竖直中心轴在水平面内匀速转动，置于AB中点P的小物体（视为质点）恰好在ABCD面上没有相对滑动。二面体的二面角为120°，截面图如图乙所示。面ABCD和面CDEF的长和宽均为，CD距水平地面的高度为，取重力加速度。

（1）求“V”型二面体匀速转动的角速度的大小；

（2）若“V”型二面体突然停止转动，求小物体从二面体上离开的位置以及小物体落地时速度的大小。

【答案】  （1）；（2），

【解析】（1）设小物体受到的支持力为F，受力如图所示。根据牛顿第二定律得

解得

（2）“V”型二面体突然停止转动，设小物体在二面体上运动的时间为t，运动的初速度大小为，加速度大小为a，沿AD方向向下运动在距离为y，则

解得

设小物体刚要到达地面时的速度大小为，由机械能守恒定律得

解得

8．（2023·辽宁·模拟预测）小李同学站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球恰好能在竖直平面内做完整的圆周运动。再次加速甩动手腕，当球某次运动到最低点A时，绳恰好断掉，如题图所示。已知握绳的手离地面高度为2L，手与球之间的绳长为L，绳能承受的最大拉力为9mg，重力加速度为g，忽略手的运动半径和空气阻力。求：

（1）为使小球能在竖直平面内作完整的圆周运动，小球过最高点B时的最小速度；

（2）绳断时球的速度大小；

（3）绳断后，小球落地点与抛出点A的水平距离。

【答案】  （1）；（2）；（3）

【解析】（1）为使小球能在竖直平面内作完整的圆周运动，小球过最高点B时，当

得

小球过最高点B时的最小速度。

（2）绳断时

绳断时球的速度大小

（3）绳断后，小球做平抛运动，竖直方向

得

小球落地点与抛出点A的水平距离

9．（2023·福建漳州·统考二模）如图甲为生产流水线上的水平皮带转弯机，由一段直线皮带和一段圆弧皮带平滑连接而成，其俯视图如图乙所示，虚线ABC是皮带的中线，AB段（直线）长度L=3.2m，BC段（圆弧）半径R=2.0m，中线上各处的速度大小均为v=1.0m/s。某次转弯机传送一个质量m=0.5kg的小物件时，将小物件轻放在直线皮带的起点A处，被传送至B处，滑上圆弧皮带上时速度大小不变，已知小物件与两皮带间的动摩擦因数均为μ=0.5，设最大静摩擦力等于滑动摩擦力，重力加速度g取10m/s2。

（1）求小物件在直线皮带上加速过程的位移大小s；

（2）计算说明小物件在圆弧皮带上是否打滑？并求出摩擦力大小。

【答案】  （1）0.1m；（2）不打滑，0.25N

【解析】（1）在直线皮带上对小物件分析有

假设物件能够匀加速至v，则有

解得

可知，物件在直线段落还有一段匀速过程，则有

（2）假设物件在圆弧处不打滑，则所需向心力为

物件与皮带之间的最大静摩擦力为

可知假设成立，且摩擦力为

10．（2023·上海黄浦·上海市大同中学统考一模）如图所示的装置由安装在水平台面上的高度H可调的斜轨道KA、水平直轨道AB、圆心为O1的竖直半圆轨道BCD、圆心为O2的竖直半圆管道DEF、水平直轨道FG等组成，F、D、B在同一竖直线上，轨道各部分平滑连接，已知滑块（可视为质点）从K点静止开始下滑，滑块质量m = 0.1kg，轨道BCD的半径R = 0.8m，管道DEF的半径r = 0.1m，滑块与轨道FG间的动摩擦因数μ = 0.4，其余各部分轨道均光滑且无能量损失，轨道FG的长度L = 3m，g取10m/s2。

（1）若滑块恰能过D点，求高度H的大小；

（2）若滑块在运动过程中不脱离轨道，求经过管道DEF的最高点F时的最小速度；

（3）若滑块在运动过程中不脱离轨道且最终能静止在水平轨道FG上，求可调高度H的范围。

【答案】  （1）2m；（2）2m/s；（3）2m ≤ H < 3m

【解析】（1）恰能过D点时，由牛顿第二定律可得

则恰能过BCD的最高点D的最小速度为

从释放到D点过程，以AB所在平面为零势能面，据机械能守恒定律可得

解得

H = 2m

（2）滑块在运动过程中不脱离轨道，则通过轨道BCD的最高点D的最小速度为

DF过程，以D所在平面为零势能面，据机械能守恒定律可得

解得

vF = 2m/s

经半圆管道的F点时，若vF > 0，滑块即可通过F点，则经过管道DEF的最高点F时的最小速度vF = 2m/s。

（3）保证不脱离轨道，滑块在F点的速度至少为vF = 2m/s，若以此速度在FG上滑行直至静止运动时，有

μmg = ma

则加速度大小为

a = μg = 0.4 × 10m/s2 = 4m/s2

H = 2m时，FG上滑行距离为

，不掉落轨道

若滑块恰好静止在G点，根据公式v2－v02 = 2ax，可得F点的最大速度为

从K释放到F点过程，以AB所在平面为零势能面，据机械能守恒定律可得

解得

滑块不脱离轨道且最终静止在轨道FG上，可调高度H的范围应满足

2m ≤ H < 3m

11．（2023·山东滨州·高三统考期末）如图，轨道固定在竖直平面内，为直线，倾角，为一段圆弧，为圆心，圆弧的半径，为圆弧的最高点，直线与圆弧相切于点，点距离地面的高度为。一质量为的物体（可视为质点）从点由静止开始沿着轨道下滑。已知物体与轨道之间的动摩擦因数为，圆弧光滑，取10m/s2。在物体运动过程中，求：

（1）物体对圆弧轨道点压力的大小；

（2）物体离开轨道后离地面的最大高度。

【答案】  （1）；（2）

【解析】（1）从点到点的过程中，设A、B之间的距离为x，则根据动能定理得

根据几何关系

摩擦力大小为

在点，根据牛顿第二定律得

根据牛顿第三定律，物体对轨道的压力大小为

（2）假设物体能到达C点，则C点速度满足

解得所需要的向心力为

故不可能到达C点，设物体在圆弧轨道的点离开，此时圆弧轨道对物体的压力为零，设与圆心的连线与竖直方向的角度为，根据牛顿第二定律

从到的过程中，根据动能定理

从点离开轨道后，物体做斜抛运动，竖直方向上达到最高高度满足

解得

物体离地面的高度为

联立解得

12．（2023·江苏南通·高三统考期末）如图所示，在竖直轴OO′的B点套有不可上下滑动，只可以绕轴无摩擦转动的轻环，轻弹簧的上端与该环相连，光滑杆OA与水平面间的夹角α=60°，质量为m的小球套在光滑杆OA上并与弹簧的下端连接，已知轴OB间距为L。

（1）保持杆不动，小球在图示P点位置处于静止状态，图示β=30°，求小球所受弹簧的弹力大小T和所受杆的弹力大小N；

（2）保持光滑杆OA与水平面间的夹角始终为α，使小球随杆OA一起由静止绕OO′轴加速转动，小球缓慢运动到与B点在同一水平面的A点时，杆OA匀速转动，小球与杆保持相对静止，求此时杆OA绕OO′轴转动的角速度大小ω；

（3）在（2）情形之下，小球由P点开始相对杆向上滑动到A点与杆相对静止的过程中，杆对球所做的功W。

【答案】  （1），mg；（2）；（3）1.5mgL

【解析】（1）小球在位置P处静止时， 受力分析，如图

根据平衡条件有

解得

，

（2）小球在位置A处时，设小球做圆周运动的半径为r，所受弹簧的弹力大小FT和杆的弹力大小FN，则水平方向

竖直方向

几何关系

弹簧伸长的长度与初始相同，则

解得

（3）小球将由静止开始沿杆向上滑动，初速度

vP=0

小球在位置A的速度大小

小球由P到A过程，根据动能定理有

解得

（2022·福建·高考真题）清代乾隆的《冰嬉赋》用“躄躠”（可理解为低身斜体）二字揭示了滑冰的动作要领。短道速滑世界纪录由我国运动员武大靖创造并保持。在其创造纪录的比赛中，

（1）武大靖从静止出发，先沿直道加速滑行，前用时。该过程可视为匀加速直线运动，求此过程加速度大小；

（2）武大靖途中某次过弯时的运动可视为半径为的匀速圆周运动，速度大小为。已知武大靖的质量为，求此次过弯时所需的向心力大小；

（3）武大靖通过侧身来调整身体与水平冰面的夹角，使场地对其作用力指向身体重心而实现平稳过弯，如图所示。求武大靖在（2）问中过弯时身体与水平面的夹角的大小。（不计空气阻力，重力加速度大小取，、、、）

【答案】  （1）；（2）；（3）

【解析】（1）设武大靖运动过程的加速度大小为，根据

解得

（2）根据

解得过弯时所需的向心力大小为

（3）设场地对武大靖的作用力大小为，受力如图所示

根据牛顿第二定律可得

解得

可得