新教材2023年高中数学第5章三角函数5.4三角函数图象与性质5.4.1正弦函数余弦函数的图象课件新人教A版必修第一册

这是一份新教材2023年高中数学第5章三角函数5.4三角函数图象与性质5.4.1正弦函数余弦函数的图象课件新人教A版必修第一册，共47页。

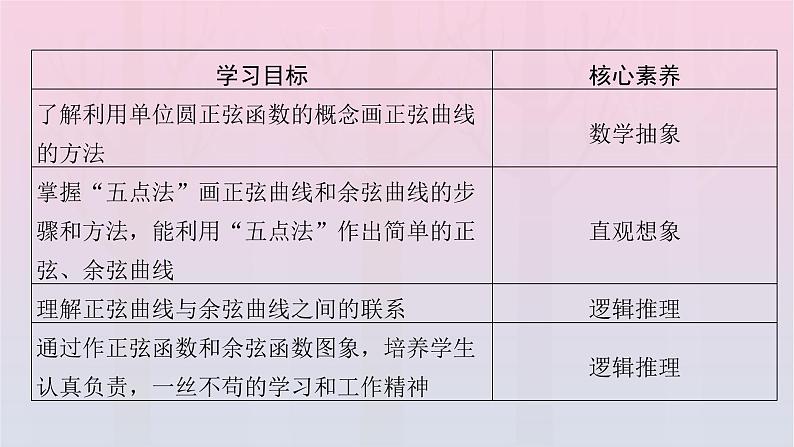
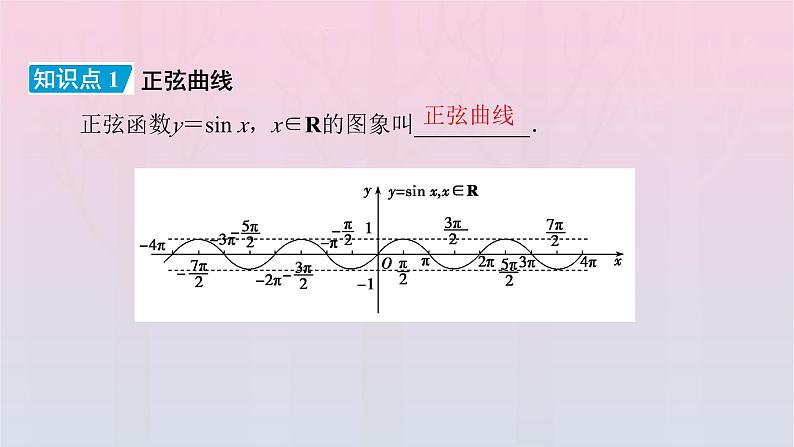
第五章　三角函数5.4　三角函数图象与性质5.4.1　正弦函数、余弦函数的图象必备知识 · 探新知正弦函数y＝sin x，x∈R的图象叫__________．正弦曲线　知识点 1正弦曲线想一想：作正弦函数的图象时，函数自变量(x)应使用什么作单位？为什么？提示：作正弦函数的图象时，函数自变量要用弧度制，以保证自变量与函数值都为实数．练一练：在同一平面直角坐标系内，函数y＝sin x，x∈[0，2π]与y＝sin x，x∈[2π，4π]的图象 (　　)A．重合B．形状相同，位置不同C．关于y轴对称D．形状不同，位置不同[解析]　根据正弦曲线的作法过程，可知函数y＝sin x，x∈[0，2π]与y＝sin x，x∈[2π，4π]的图象位置不同，但形状相同．B　(1)几何法：①利用正弦线画出y＝sin x，x∈[0，2π]的图象；知识点 2正弦函数图象的画法②将图象向左、向右平行移动(每次2π个单位长度)．想一想：观察上图，你认为正弦曲线是如何画出来的？提示：利用单位圆中的正弦线可以作出y＝sin x，x∈[0，2π]的图象，将y＝sin x在[0，2π]内的图象左右平移即可得到正弦曲线．五个关键点　A　B　余弦函数y＝cos x，x∈R的图象叫余弦曲线．知识点 3余弦曲线想一想：你认为应该利用正弦函数和余弦函数的哪些关系，通过怎样的图形变换，才能将正弦函数的图象变换为余弦函数的图象？提示：诱导公式　左右平移B　知识点 4余弦函数图象的画法想一想：正弦曲线和余弦曲线有怎样的关系？练一练：对于正弦函数y＝sin x的图象，下列说法错误的是 (　　)A．过原点B．与y＝cos x的图象形状相同，只是位置不同C．与x轴有无数个交点D．关于y轴对称D　关键能力 · 攻重难 用“五点法”作出下列函数的简图：(1)y＝sin x－1，x∈[0，2π]；(2)y＝2＋cos x，x∈[0，2π]．[分析]　先在[0，2π]上找出五个关键点，再用光滑曲线连接即可．典例1[解析]　(1)列表描点，连线，如图[归纳提升]　用“五点法”画函数y＝Asin x＋b(A≠0)或y＝Acos x＋b(A≠0)在[0，2π]上的简图的步骤：(1)列表：【对点练习】❶ 用“五点法”画出下列函数在区间[0，2π]上的简图．(1)y＝2－sin x；(2)y＝cos x－1.描点并将它们用光滑的曲线连接起来(如图(1))． 利用图象变换作出下列函数的简图：(1)y＝1－cos x，x∈[0，2π]；(2)y＝|sin x|，x∈[0，4π]．[分析]　先作出y＝cos x和y＝sin x，x∈[0，2π]上的图象，再作对称和平移变换．典例2[解析]　(1)首先用五点法作出函数y＝cos x，x∈[0，2π]的图象，再作出y＝cos x关于x轴对称的图象，最后将图象向上平移1个单位．如图(1)所示．(2)首先用五点法作出函数y＝sin x，x∈[0，4π]的图象，再将x轴下方的部分对称到x轴的上方．如图(2)所示．[归纳提升]　1．平移变换(1)函数y＝f(x＋a)的图象是由函数y＝f(x)的图象向左(a>0)或向右(a<0)平移|a|个单位得到的．(2)函数y＝f(x)＋b的图象是由函数y＝f(x)的图象向上(b>0)或向下(b<0)平移|b|个单位得到的．2．对称变换(1)函数y＝|f(x)|的图象是将函数y＝f(x)的图象在x轴上方的部分不动，下方的部分对称翻折到x轴上方得到．(2)函数y＝f(|x|)的图象是将函数y＝f(x)的图象在y轴右边的部分不动，并将其对称翻折到y轴左边得到．(3)函数y＝－f(x)的图象与函数y＝f(x)的图象关于x轴对称．(4)函数y＝f(－x)的图象与函数y＝f(x)的图象关于y轴对称．(5)函数y＝－f(－x)的图象与函数y＝f(x)的图象关于原点对称．D　利用正弦函数、余弦函数图象判断方程根的个数C　典例3 方程sin x＝lg x的实根个数有 (　　)A．1个　　　　 B．2个C．3个 D．无穷多个[错解]　如图所示，y＝sin x与y＝lg x的图象，有且只有1个公共点，故选A．[错因分析]　作y＝lg x图象时，没有找准临界点的坐标，只作出了草图．[正解]　在同一直角坐标系中作函数y＝sin x与y＝lg x的图象．由图中可以看出两函数图象有三个交点(xi，yi)，其中xi∈(1，10)(i＝1，2，3)是方程sin x＝lg x的解．[方法点拨]　有些方程从正面直接求解较难时，可通过对方程变形，转化成两个熟悉的函数，再通过画函数图象，利用数形结合求解．利用正、余弦函数的图象解不等式典例4[归纳提升]　用三角函数图象解三角不等式的步骤(1)作出相应的正弦函数或余弦函数在[0，2π]上的图象．(2)写出适合不等式在区间[0，2π]上的解集．(3)根据公式一写出定义域内的解集．课堂检测 · 固双基A　D　C　B　5．用“五点法”作出下列函数的简图：(1)y＝－sin x(0≤x≤2π)；(2)y＝1＋cos x(0≤x≤2π)．描点作图，如图．描点作图，如图．