
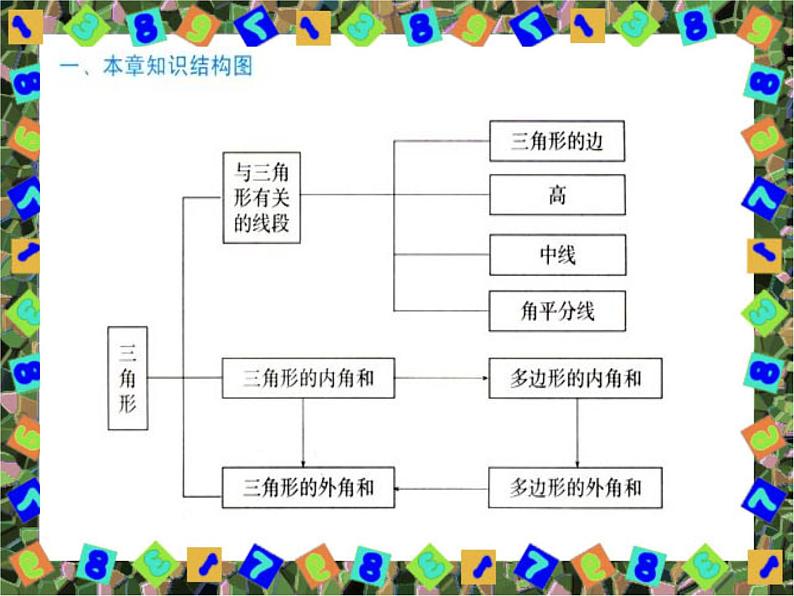



初中数学青岛版七年级下册13.1 三角形复习ppt课件
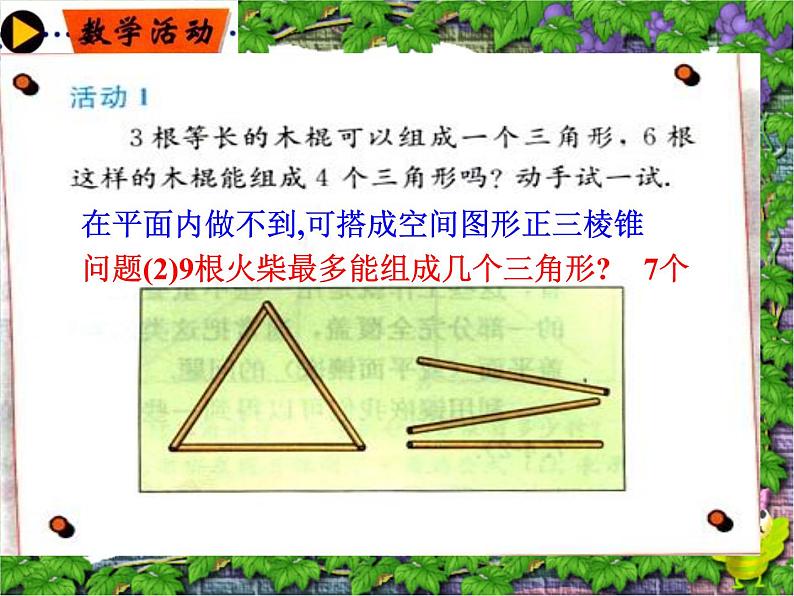
展开问题(2)9根火柴最多能组成几个三角形?
在平面内做不到,可搭成空间图形正三棱锥
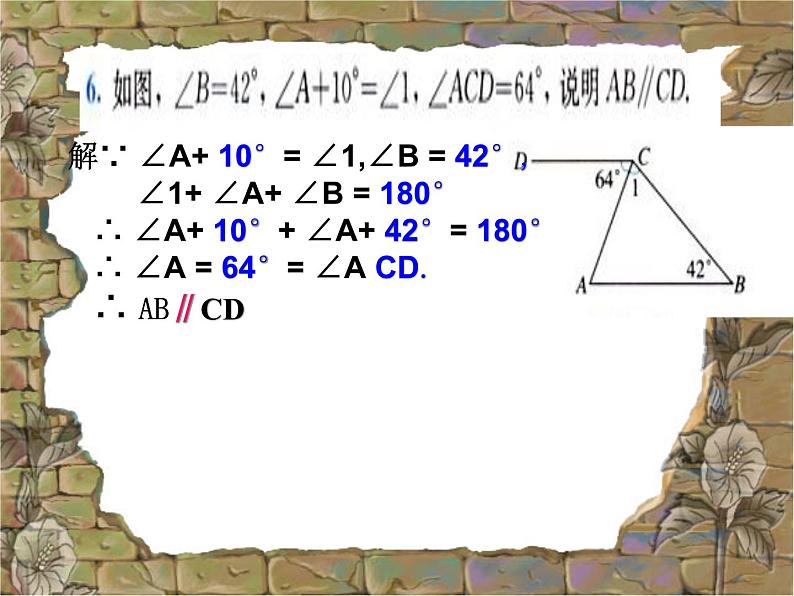
解∵ ∠A+ 10°= ∠1,∠B = 42°, ∠1+ ∠A+ ∠B = 180° ∴ ∠A+ 10°+ ∠A+ 42°= 180° ∴ ∠A = 64°= ∠A CD. ∴ AB∥CD
解∵ ∠C=∠ABC=2∠A ∠A +∠ABC+∠C= 180°∴ 5∠A = 180°∴ ∠A = 36°∴ ∠C= 72°∵BD是AC边上的高,∴ ∠DBC= 180°- 90°- 72°=18°
解∵AD是△ABC的高, ∠C= 70°∴ ∠DAC= 180°- 90°- 70°= 20°∵ ∠BAC= 50°∴ ∠ABC= 180°- 50°- 70°= 60°∵ AE 和BF是角平分线∴ ∠BAO=25°, ∠ABO=30°∴ ∠AOB= 180°- 25°- 30°= 125°
解:正五边形的每个内角是108°正六边形的每个内角是120°.三块皮块有一个公共顶点.位于公共顶点处的三个内角分别是108°, 120°, 120°,它们的和是348°,小于360°.所以不能将这三块皮块连在一起铺平.
1.已知等腰三角形的两边长分别为10和6,则三角形的周长为________2.等腰三角形的两边和与差分别为16和8,则此三角形的周长为______ 3.以线段3、4、x-5为边组成三角形,那么x的取值范围是_________ 4.若三角形的两边长分别为4、a(a>0),则第三边的取值范围是____
5.两根木棒长分别为5和7,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,则第三根木棒的取值情况有___种6.等腰三角形的周长为18厘米,若腰长是底边的2倍,则三边的长分别是 、 、 若已知其中一边的长为4厘米,则其它两边的长为 、____
7.如图:0为△ABC内一点,求证:(1)OB +OA +OC﹥ (AB +AC +BC)(2)OB+OC<AB+AC(3)OA+OB+OC<AB+BC+AC
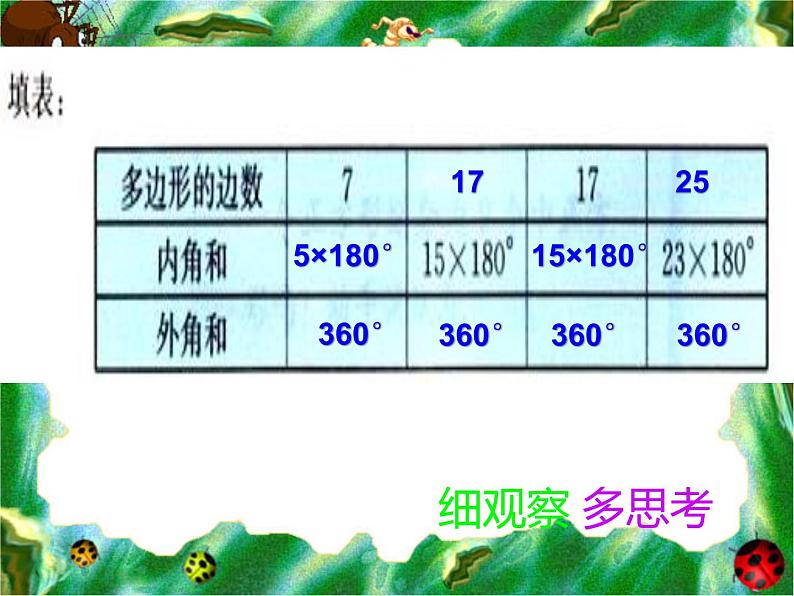
回顾二:1.锐角三角形、钝角三角形、直角三角形定义2.三角形的外角的定义3.三角形内角和定理及推论1、2、34.三角形按角的分类
1.直角三角形的两锐角的关系_______2.直角三角形的两个锐角的平分线的夹角是 .3.三角形ABC中,∠B=∠C=2∠A,则∠B= ,∠A=_______4.在△ABC中 已知: ∠A:∠B:∠C =1:2:3,则三角形是____三角形; 若∠A+∠B=∠C,则此三角形是________ 三角形
5.(1)在直角三角形中,一个锐角是30°,则另一个锐角的外角是______(2)直角三角形的一个锐角是另一个锐角的3倍,这两个锐角分别是______ (3)三角形的一个外角等于与相邻内角的4倍,等于与它不相邻的一个内角的2倍,则三角形的各角的度数是___
6.在△ABC中,最大角A是最小角C的3倍,且∠A 与∠B的差等于∠B与∠C 的差,则∠A= ,∠B= ,∠C=_____;7.在△ABC中,已知:3∠A=∠C,3∠B=2∠C,则 △ABC是 三角形;8.已知:三角形ABC中,∠C=∠ABC =2∠A,BD是AC边上的高,则∠DBC= _______
9.叙述并证明三角形的内角和定理。
10.如图,已知DE分别交△ABC的边AB、AC于D、E,交BC的延长线于F,∠B=67O,∠ACB=740,∠AED=480,则∠BDF=________
12.如图:求证:∠A+∠B+∠C=∠ADC
11. 已知:P是三角形ABC内任意一点 求证:∠BPC>∠A
13.如图:D是△ACB的外角平分线CD与BA的延长线的交点,求证:∠BAC>∠B
14.△ABC中,∠ABC的平分线BD和△ABC的外角平分线CD交于D,求证:∠A=2∠BDC
15.如图,D、E为△ABC内的两点 求证:AB+AC﹥BD+DE+EC
青岛版七年级下册13.1 三角形精品ppt课件: 这是一份青岛版七年级下册13.1 三角形精品ppt课件,共20页。
人教版七年级下册10.2 直方图精品ppt课件: 这是一份人教版七年级下册10.2 直方图精品ppt课件,共15页。PPT课件主要包含了知识回顾,各方法有什么特点,频数组距,身高㎝等内容,欢迎下载使用。
数学七年级下册10.2 直方图优质ppt课件: 这是一份数学七年级下册10.2 直方图优质ppt课件,共11页。PPT课件主要包含了知识回顾,问题2等内容,欢迎下载使用。













