





初中数学青岛版七年级下册第13章 平面图形的认识13.1 三角形试讲课课件ppt
展开1.通过作图、对折、思考等,能够理解并能口述出等腰三角形的概念,能够发现等腰三角形的轴对称性;
2.通过对折、合作交流等,探究出等腰三角形的对称轴是底边的垂直平分线,由此推理并证明得到等腰三角形的性质定理,并能够利用性质定理解决实际问题;
3.通过回忆线段垂直平分线的作法以及等腰三角形三线合一性质,能够完成基本作图:已知底边和底边上的高,求作等腰三角形三角形
做一个等腰三角形,折一折,并思考一下问题:
1.△ABC是轴对称图形吗?对称轴AD是底边BC的 线?
2.①∠BAD与∠CAD是什么关系?AD是顶角∠BAC的 线? ②因为AD⊥BC,所以AD也是底边BC上的 线? ③因为BD=CD,所以D是BC的 点,所以AD也是底边BC上的 线(点拨:连接顶点与对边中点的线段为三角形的中线)
3.底角∠B与∠C相等吗?
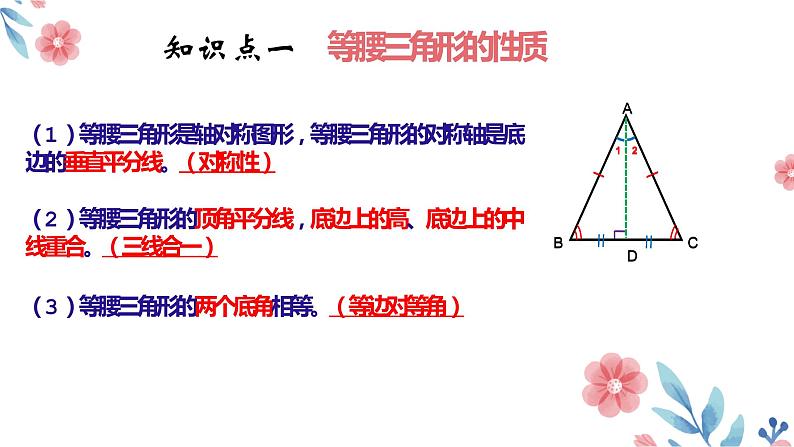
知识点一 等腰三角形的性质
(1)等腰三角形是轴对称图形,等腰三角形的对称轴是底边的垂直平分线。(对称性)
(2)等腰三角形的顶角平分线,底边上的高、底边上的中线重合。(三线合一)
(3)等腰三角形的两个底角相等。(等边对等角)
1.等腰三角形的顶角的平分线,既是底边上的中线,又是底边上的高。
符号语言:∵AB=AC ∠BAD=∠CAD(已知)
2.等腰三角形的底边上中线,既是底边上的高,又是顶角平分线。
符号语言: ∵AB=AC BD=DC (已知)
3.等腰三角形的底边上的高,既是底边上的中线,又是顶角平分线。
符号语言: ∵AB=AC AD⊥BC (已知)
三线合一符号语言运用:
∴BD=DC AD⊥BC(等腰三角形三线合一)
∴AD⊥BC ∠BAD=∠CAD (等腰三角形三线合一)
∴BD=DC ∠BAD=∠CAD (等腰三角形三线合一)
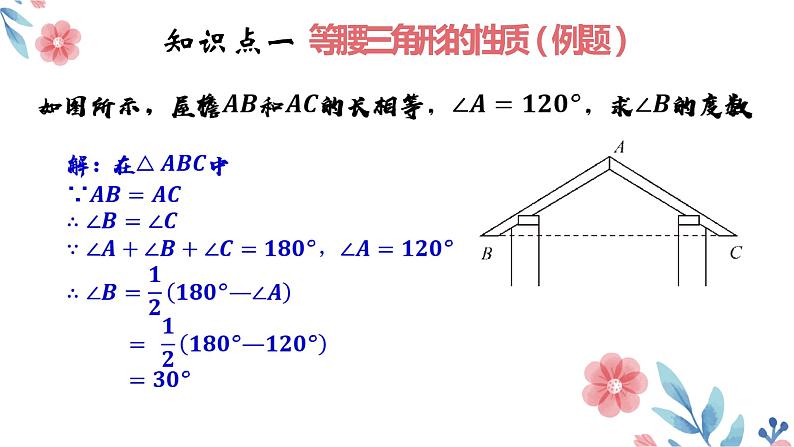
知识点一 等腰三角形的性质(例题)
知识点一 等腰三角形的性质(应用)
6.如图,在△ABC中,AB=AC,AE是BC边上的高,BD为AC边上的高,已知∠EAD=20°,则∠ABD的度数是( )。A.20° B.40° C.50° D.70°
5.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
思考:顶角是直角的三角形叫做等腰直角三角形。等腰直角三角形的底角为多少度?
1.通过尺规作出有两个角相等的三角形,并通过折叠所作三角形,探究并总结归纳出得到等腰三角形的判定定理的文字和符号语言;
2.通过对例题的学习与研究,能够熟练运用等腰三角形的判定定理解决实际问题
思考:1.在作出的三角形中,用圆规比较AB与AC的长,你会发现什么?2.根据你的发现,△ABC是什么三角形?3.通过刚刚的操作与发现,你能总结出如何判定一个三角形是等腰三角形吗?
知识点二 等腰三角形的判定
★等腰三角形的判定:有两个角相等的三角形是等腰三角形
你能用学过的知识证明上面的结论吗?
知识点二 等腰三角形的判定(证明)
点拨:可以过哪个点做辅助线?做辅助线的种类有哪些?
知识点二 等腰三角形的判定(应用)
模型:角平分线+平行线→等腰三角形
1.通过对等腰三角形与等边三角形的观察与分析,能够理解等腰三角形与等边三角形的关系,能够总结归纳出:等边三角形具有等腰三角形的一切性质;
2.通过回顾三角形内角和,能够计算并得到等边三角形的性质定理,并能利用性质定理解决实际问题;
3.通过对不同三角形的分析以及合作交流等,能够总结归纳出等边三角形的判定定理,并能够利用判定定理解决实际问题。
知识点一 等边三角形的定义
三边都相等的三角形是等边三角形
知识点二 等边三角形的性质
(3)等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质
(2)等边三角形是轴对称图形,它有三条对称轴,三条对称轴的交点称为“中心”
知识点三 等边三角形的判定
一个三角形满足什么条件就是等边三角形?
1.三条边都相等的三角形是等边三角形.
2. 三个角都相等的三角形是等边三角形.
有一个角是60°的等腰三角形是等边三角形.
等腰三角形满足什么条件就是等边三角形?
(1)三条边都相等的三角形是等边三角形(2)三个角都相等的三角形是等边三角形(3)有一个角是60°的等腰三角形是等边三角形
(2)第三种判定方法是在等腰三角形的条件下, 60°的角无论是顶角还是底角都成立
(1)“三个角都相等的三角形是等边三角形”也可理解为 “有两个内角等于60°的三角形是等边三角形”
知识点三 等边三角形的判定(应用)
1.下面的判断中,错误的是( )A.在△ABC中,如果AB=AC,且∠A=∠B,那么△ABC是等边三角形B.在△ABC中,如果AB=AC,且∠B=∠C,那么△ABC是等边三角形C.在△ABC中,如果∠A=60°,∠B=60°,那么△ABC是等边三角形D.在△ABC中,如果AB=AC,∠B=60°,那么△ABC是等边三角形
2.如图,△ABC是等边三角形,BC边上的中线AD与AC边上的中线BE相交与点O,求∠DOE的度数,你有几种不同的求法?
3.如图,△ABC为等边三角形,∠1=∠2=∠3(1)求∠BEC的度数;(2)△DEF是等边三角形吗?为什么?
青岛版八年级上册2.6 等腰三角形教学课件ppt: 这是一份青岛版八年级上册2.6 等腰三角形教学课件ppt,共19页。PPT课件主要包含了猜谜语,三角形,学习目标,“三线合一”,用符号语言表示为,等边对等角,等腰三角形的性质3,例题讲解,°或80°,本节课你学到了什么等内容,欢迎下载使用。
青岛版八年级上册2.6 等腰三角形精品ppt课件: 这是一份青岛版八年级上册2.6 等腰三角形精品ppt课件,共17页。PPT课件主要包含了知识回顾,等边对等角,三线合一,等角对等边,两边相等,两腰相等,轴对称图形,“三线合一”的逆用,等边三角形的性质,试一试等内容,欢迎下载使用。
初中数学青岛版八年级上册2.6 等腰三角形公开课ppt课件: 这是一份初中数学青岛版八年级上册2.6 等腰三角形公开课ppt课件,共15页。PPT课件主要包含了这就是说,方法1,方法2,方法3,几何语言表示如下,等腰三角形的判定方法,理由在△ABC中,∴∠B∠C70°等内容,欢迎下载使用。













