第3章 实数 小结与复习 南阳2中2022年湘教版八年级上册数学 课件

这是一份第3章 实数 小结与复习 南阳2中2022年湘教版八年级上册数学 课件，共13页。

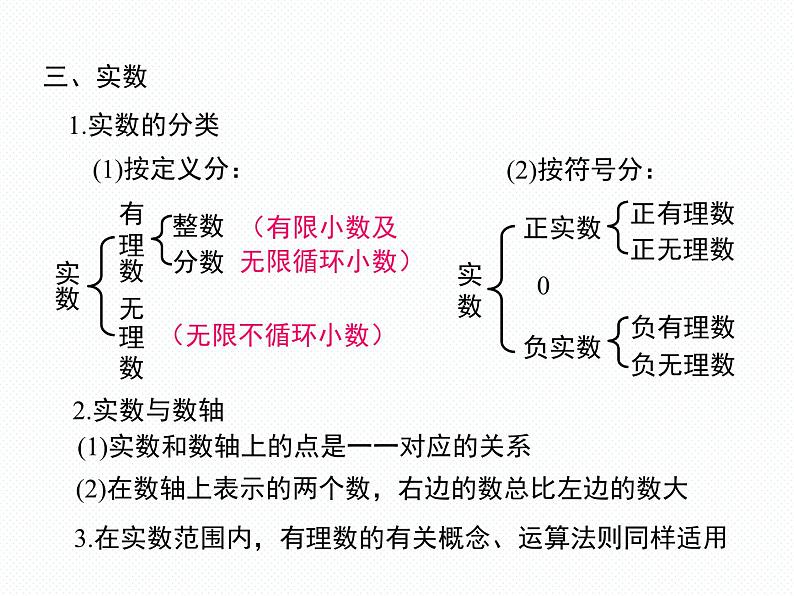
第3章 实 数小结与复习要点梳理1. 平方根的概念及性质2. 算术平方根的概念及性质3. 无理数(2)性质：正数a有两个平方根，它们互为相反数； 0的平方根是0，负数没有平方根.(2)性质：0的算术平方根是0，只有非负数才有算术平 方根，而且算术平方根也是非负数.一、平方根(1)定义：若r2=a，则r叫作a的一个平方根.(1)定义：a的正平方根叫作a的算术平方根.常见类型：带根号且开不尽方的数；含π的一些数； 无限不循环小数.1. 立方根的概念及性质(1)定义：如果b3=a，那么b叫作a的立方根.二、立方根(2)性质：每一个实数都有一个与它本身符号相同的 立方根.2. 用计算器求立方根 用计算器求一个数a的立方根，其按键顺序为三、实数1.实数的分类(1)按定义分：(2)按符号分：2.实数与数轴(1)实数和数轴上的点是一一对应的关系(2)在数轴上表示的两个数，右边的数总比左边的数大3.在实数范围内，有理数的有关概念、运算法则同样适用 例1 已知一个正数的两个平方根分别是a+3和2a-18，求这个正数.【解析】根据一个正数的平方根有两个，它们互为相反数，可以得到关于a的一元一次方程，解之求得a的值，从而可求出这个正数.解：根据平方根的性质，有a+3+2a-18=0，解得a=5，a+3=8，82=64，所以这个正数是64. 一个正数的平方根有两个，它们互为相反数．而一个非负数的算术平方根只有一个.另外，一个数的立方根也只有一个，且与它本身的符号相同.BC-111CAC【解析】数轴上的点表示的数，右边的总比左边的大，故A不正确；根据点A，B与原点的距离知|a|<|b|，B不正确；-a>0，根据|a|<|b|，知-a