

2023年贵阳初中学业水平考试数学模拟卷(一)含答案
展开2023年贵阳初中学业水平考试数学模拟卷(一)
(考试时间:120分钟 满分:150分)
姓名:__________ 班级:__________ 分数:__________
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,每小题3分,共36分.
1.下列四个数中,最小的数是(D)
A.0 B.2 C.-1 D.-3
2.围成下列立体图形的各个面中,每个面都是曲的是(C)
A B C D ,
3.地球静止轨道卫星的静止轨道与地面的高度约为35 800 km.将35 800用科学记数法表示为(A)
A.3.58×104 B.0.358×104 C.3.58×105 D.0.358×105
4.如图,直线AB,CD交于点O.射线OM平分∠AOC,若∠BOD=68°,则∠COM的度数为(B)
A.36° B.34° C.32° D.26°
,
, 第4题图 第6题图 第8题图 ,
5.分式方程+1=的解是(D)
A.x=1 B.x=-2 C.x= D.x=2
6.如图,在▱ABCD中,CD=8,BC=10,按以下步骤作图:①以点C为圆心,适当长度为半径作弧,分别交BC,CD于M,N两点;②分别以点M,N为圆心,以大于MN的长为半径画弧,两弧在▱ABCD的内部交于点P;③连接CP并延长交AD于点E,交BA的延长线于点F,则AF的长为(A)
A.2 B.3 C.4 D.5
7.若四边形ABCD是菱形,其中AB=4 cm,则四边形ABCD的周长是(D)
A.5 cm B.8 cm C.12 cm D.16 cm
8.把下列无理数表示在数轴上,被墨迹(如图所示)覆盖住的无理数是(B)
A. B. C. D.-
9.下表是某社团15名同学的捐款情况,下列说法中正确的是(B)
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A.众数是100 B.中位数是30
C.方差是20 D.平均数是30
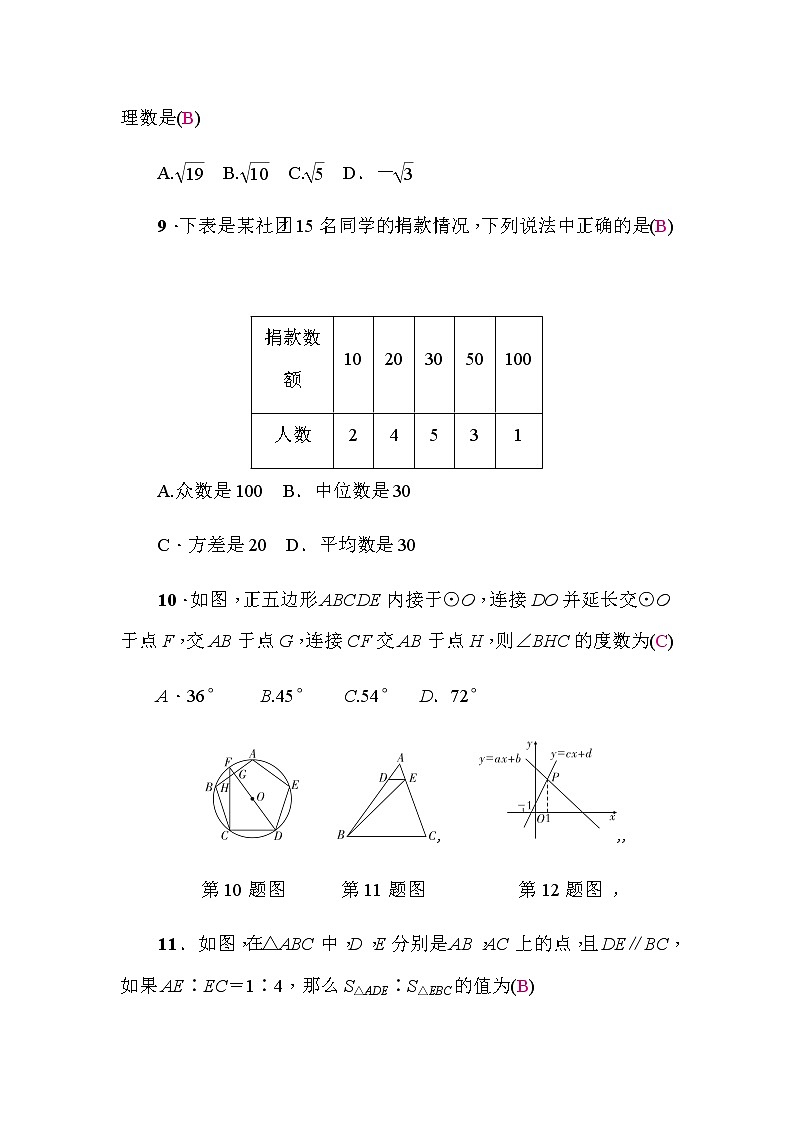
10.如图,正五边形ABCDE内接于⊙O,连接DO并延长交⊙O于点F,交AB于点G,连接CF交AB于点H,则∠BHC的度数为(C)
A.36° B.45° C.54° D.72°
, ,,
第10题图 第11题图 第12题图 ,
11.如图,在△ABC中,D,E分别是AB,AC上的点,且DE∥BC,如果AE∶EC=1∶4,那么S△ADE∶S△EBC的值为(B)
A.1∶24 B.1∶20 C.1∶18 D.1∶16
12.★如图,一次函数y=ax+b与y=cx+d的图象交于点P.下列结论:①b<0;②ac<0;③当x>11时,ax+b>cx+d;④a+b=c+d;⑤c>d.其中正确结论的个数是(C)
A.1 B.2 C.3 D.4
二、填空题:每小题4分,共16分.
13.已知m2-2m=1,则3+m2-2m=4.
14.《九章算术》是中国古代数学著作之一,书中有这样的一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换一只,恰好一样重.问:每只雀、燕的质量各为多少?设一只雀的质量为x斤,一只燕的质量为 y斤,则可列方程组为.
15.一次购物中,小马和小张都随机从“微信”、“支付宝”、“银行卡”、“云闪付”四种支付方式中选一种方式进行支付,两位恰好一人用“微信”支付,一人用“支付宝”支付的概率是.
16.★如图,过正方形ABCD的中心O的直线分别交DC,AB于点E,F,将该正方形沿直线EF折叠,点A,D分别落在点A′,D′的位置,连接A′C.若AB=6,DE=1,则OE=,A′C=
.
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(本题满分12分)(1)化简:(x+2)2-x(1+x);
解:原式=x2+4x+4-x-x2 =3x+4.
(2)给三个分式:,,,请把这三个分式(次序自定)填入下列横线上(________-________)÷________,并化简.
解:答案不唯一,例如:
÷=·
=·=.
18.(本题满分10分)为了了解某市初中生的视力情况,随机抽取了3 000名学生进行检测,收集数据后,绘制了以下三幅统计图表,请根据图表中提供的信息解答下列问题:
| 调查人数 | 视力不良 | 视力不良率(精确到0.01) |
男生 | 1 400 | 750 | 54% |
女生 | 1 600 | m | n |
根据统计图表回答下列问题:
(1)统计表中m=1 050,n=66%;
(2)补全条形统计图,并通过计算估计该市80 000名初中生的视力不良情况的人数;
(3)通过统计图表中的信息,写出一条关于视力不良的正确结论.
解:(2)补全条形统计图如图所示.估计该市视力不良人数为48 000人.(3)视力不良人数成逐年增长趋势.
19.(本题满分10分)如图,▱ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接EB,DF.判断四边形EBFD的形状,并说明理由.
(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,∴OE=OF,
在△DOE和△BOF中,
∴△DOE≌△BOF(SAS).
(2)解:结论:四边形EBFD是矩形.理由:∵OD=OB,OE=OF,
∴四边形EBFD是平行四边形,∵BD=EF,∴四边形EBFD是矩形.
20.(本题满分10分)如图,一次函数y1=kx+b的图象与x轴,y轴分别交于点A,B,与反比例函数y2=(m>0)的图象交于点C(1,2),D(2,n).
(1)分别求出两个函数的解析式;
(2)连接OD,求△BOD的面积.
解:(1)∵y2=过点C(1,2)和点D(2,n),
∴m=2,n=1,∴y2=,D(2,1),
∵y1=kx+b过点C(1,2)和点D(2,1),
∴解得∴y1=-x+3.
(2)由y1=-x+3过点B,可知B(0,3),
∴△BOD的面积为×3×2=3.
21.(本题满分10分)我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点A处测得阿育王塔最高点C的仰角∠CAE=45°,再沿正对阿育王塔方向前进至B处测得最高点C的仰角∠CBE=53°,AB=10 m;小亮在点G处竖立标杆FG,小亮的所在位置点D、标杆顶F、最高点C在一条直线上,FG=1.5 m,GD=2 m.(注:结果精确到0.01 m,参考数据:sin 53°≈0.799,cos 53°≈0.602,tan 53°≈1.327)
(1)阿育王塔的高度CE约为40.58m;
(2)求小亮与阿育王塔之间的距离ED.
解:(2)由题意知Rt△FGD∽Rt△CED,
∴=,即=,∴ED≈54.11.
经检验,ED≈54.11是方程的解,且符合题意.
答:小亮与阿育王塔之间的距离ED约为54.11 m.
22.(本题满分10分)某学校要购买甲、乙两种消毒液.若购买9桶甲消毒液和6桶乙消毒液,则一共需要615元;若购买8桶甲消毒液和12桶乙消毒液,则一共需要780元.
(1)每桶甲消毒液、每桶乙消毒液的价格分别是多少元?
(2)若该校计划购买甲、乙两种消毒液共30桶,其中购买甲消毒液a桶,且甲消毒液的数量至少比乙消毒液的数量多5桶,又不超过乙消毒液的数量的2倍.怎样购买,才能使总费用W最少?并求出最少费用.
解:(1)设每桶甲消毒液价格为x元,每桶乙消毒液的价格为y元,由题意可得解得
答:每桶甲消毒液的价格为45元,每桶乙消毒液的价格为35元.
(2)由题意可得W=45a+35(30-a)=10a+1 050,
∴W随a的增大而增大,∵甲消毒液的数量至少比乙消毒液的数量多5桶,又不超过乙消毒液的数量的2倍,∴
解得17.5≤a≤20,∵a为整数,∴当a=18时,W取得最小值,
此时W=1 230(元),30-a=12(桶).
答:购买甲消毒液18桶,乙消毒液12桶时,总费用W最少,最少费用是1 230元.
23.(本题满分12分)如图,在Rt△ABC中,∠ABC=90°,O为BC边上一点,以点O为圆心,OB长为半径的⊙O与AC边相切于点D,交BC于点E.
(1)求证:AB=AD;
(2)连接DE,若tan∠EDC=,DE=2,求线段EC的长.
(1)证明:∵∠ABC=90°,∴AB⊥OB.
∵OB是⊙O的半径,∴AB切⊙O于点B.
∵AC切⊙O于点D,∴AB=AD.
(2)解:连接BD,∵BE为⊙O的直径,
∴∠BDE=90°.∴∠CDE+∠ADB=90°,
∵AB=AD,∴∠ADB=∠ABD,∴∠CDE+∠ABD=90°,
∵∠ABC=90°,∴∠ABD+∠EBD=90°,∴∠EBD=∠EDC.
∵tan∠EDC=,∴tan∠EBD=,即=,
∵DE=2,∴BD=4,BE=2.∵∠C=∠C,∠EBD=∠EDC,
∴△CDE∽△CBD,∴===,
设CE=x,则DC=2x,∴(2x)2=x(x+2),
∴x1=0(舍去),x2=,即线段EC的长为.
24.(本题满分12分)如图,已知抛物线y=x2+bx+c分别交x轴、y轴于点A(-1,0),C(0,-3),连接AC.
(1)求该抛物线的解析式;
(2)若P(x1,y1),Q(x2,y2)是抛物线上两点,当x1≤-2,m≤x2≤m+1时,均有y1≥y2,求m的取值范围;
(3)将该抛物线向左平移n(n>0)个单位长度后,得到的新抛物线与线段AC只有一个交点,请直接写出n的取值范围.
解:(1)y=x2-2x-3.
(2)∵y=x2-2x-3=(x-1)2-4,
∴抛物线开口向上,对称轴为直线x=1,
将x=-2代入y=x2-2x-3得y=5,
∴抛物线经过点(-2,5),点(-2,5)关于对称轴的对称点为(4,5),∴-2≤m<m+1≤4,解得-2≤m≤3.
∴m的取值范围为-2≤m≤3.
(3)∵抛物线经过点A(-1,0),C(0,-3),抛物线的对称轴为直线x=1,
∴抛物线经过(3,0),(2,-3),3-(-1)=4,
∴抛物线向左平移4个单位长度经过点A,2-0=2,
∴抛物线向左平移2个单位长度经过点C,∴当2≤n≤4时,满足题意.
25.(本题满分12分)某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段进行了如下探究:
【观察与猜想】
(1)如图①,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE,BD,CE⊥BD,则的值为;
【类比探究】
(2)如图②,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE·AB=CF·AD;
【拓展延伸】
(3)如图③,在Rt△ABD中,∠BAD=90°,AD=9,tan∠ADB=,将△ABD沿BD翻折,点A落在点C处得到△CBD,点E,F分别在边AB,AD上,连接DE,CF,DE⊥CF.连接BF,若AE=1,直接写出BF的长度.
(2)证明:如图②,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,∴∠G=∠H=∠A=∠B=90°,∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,∴△DEA∽△CFH,
∴=,∴=,∴DE·AB=CF·AD.
(3)解:如图③,连接AC交BD于点H,则AH⊥BD,
∵AD=9,tan∠ADB=,∴AB=3,由勾股定理,得BD=3,
由面积法知AH===,
∵将△ABD沿BD翻折,点A落在点C处得到△CBD,
∴AC=2AH=,∵CF⊥DE,∴∠ACF=∠BDE,
∵∠HAD=∠ABD,∴△ACF∽△BDE,∴===,
∵AE=1,∴BE=2,∴AF=,∴BF===.
2023年贵阳初中学业水平考试数学模拟卷(二)含答案: 这是一份2023年贵阳初中学业水平考试数学模拟卷(二)含答案,共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中学业水平考试(中考)数学模拟测试(含答案): 这是一份初中学业水平考试(中考)数学模拟测试(含答案),共6页。试卷主要包含了09, 所有的答案必须在答题卡上作答,的相反数是,下列计算正确的是,39,乙组数据方差S乙2=0等内容,欢迎下载使用。
2022年江西省初中学业水平考试数学模拟卷一 (word版含答案): 这是一份2022年江西省初中学业水平考试数学模拟卷一 (word版含答案),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












