

初中学业水平考试(中考)数学模拟测试(含答案)
展开2023年初中学考数学模拟测试(含答案)
2022.09
注意事项:
- 全卷共6页,三大题,满分120分,考试时间为120分钟。
2. 答题前,考生务必将自己的姓名、准考证号码写在答题卡相应的位置上,并在指定的位置粘贴条形码。
3. 所有的答案必须在答题卡上作答。选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑,非选择题用黑色墨水钢笔或签字笔将答案写在答题卡规定的地方,试卷上答题无效。
一、选择题:(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的,不选,错选或多选均不得分)。
1.的相反数是( )
A. B. C. D.
2. 如图是由5个相同的正方体搭成的几何体,其左视图是( )
A. B. C. D.
3.2022年1月31日,农历除夕,中国人首次在距离地球约396000米的“中国宫”里迎新春、 过大年。神舟十三号航天员在遥远的太空专门发来视频,向祖国和人民送上祝福.数据396000 用科学记数法表示为( )
A. B. C. D.
4.下列计算正确的是( ).
A. B. C. D.
5.函数y=+中自变量x的取值范围是( )
A.x≤2 B.x=3 C.x<2且x ≠3 D.x ≤2且x≠3
6.下列说法不正确的是( )
A.了解全市中学生对合肥“大湖名城,创新高地”含义的知晓度的情况,适合用抽样调查
B.若甲组数据方差S甲2=0.39,乙组数据方差S乙2=0.27,则乙组数据比甲组数据稳定
C.某种彩票中奖的概率是,买100张该种彩票一定会中奖
D.数据﹣1、1.5、2、2、4的中位数是2
7.新冠肺炎变异病毒炎奥密克戎传染速度很快,假如有1人患了新冠肺炎,经过两轮传染后共有64人患了新冠肺.求每轮传染中平均1个人传染几个人?设每轮传染中平均1个人传染x个人,则下列方程中符合题意的是( )
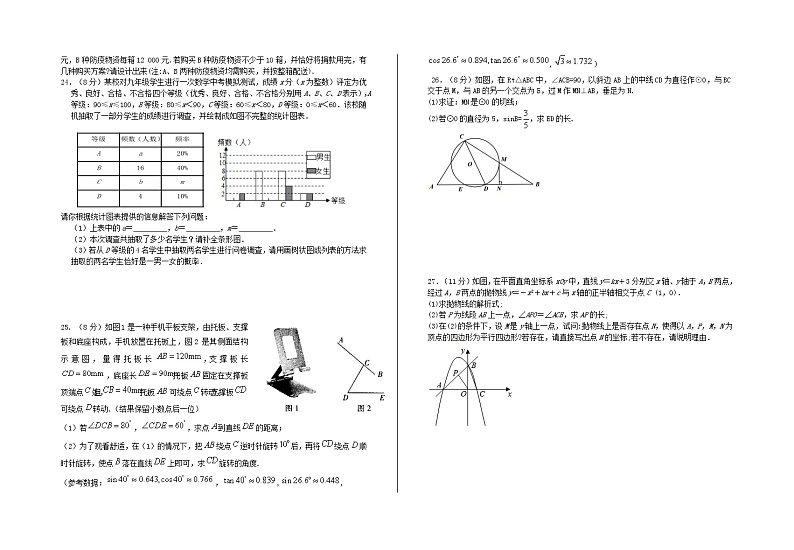
A. B. C. D.
8.已知关于的分式方程的解为非负数,则的取值范围是( )
A. B.且 C. D.且
9.如图,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠2=( ).
A.90° B.115° C.130° D.100°
10.如图,BD是⊙O的直径,点A,C在⊙O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为( )
A.99° B.108° C.110° D.117°
第9题图 第10题图 第11题图 第12题图
11.如图,在3×3的网格中,每个小正方形的边长均为1,点A、B、C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
12.如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(﹣1,0)、B(0,2)、C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A',则A'C的最小值为( )
A. B. C. D.1
二、填空题:(本大题共6小题,每小题3分,共18分)。
13.分解因式:= .
14. 邮票素有“国家名片”之称,方寸之间,包罗万象.为宣传2022年北京冬奥会,中国邮政发行了一套冬奥会邮票,其中有一组展现雪上运动的邮票,如图所示:
越野滑雪(4-1)J | 高山滑雪(4-2)J | 冬季两项(4-3)J | 自由式滑雪(4-4)J |
① | ② | ③ | ④ |
某班级举行冬奥会有奖问答活动,答对的同学可以随机抽取邮票作为奖品.在抢答环节中,若答对一题,可从4枚邮票中任意抽取1枚作为奖品,则恰好抽到“冬季两项”的概率是 ;
15.线段AB端点B的坐标分别为B(8,2),以原点O为位似中心,将线段AB缩小为原来的后得到线段CD,则端点D的坐标为 .
16.如图,某同学利用半径为40cm的扇形纸片制作成一个圆锥形纸帽(接缝忽略不计),若圆锥底面半径为10cm,那么这个圆锥的侧面积是 cm2.
17.有一列数:a1,a2,a3,a4,…,an﹣1,an,其中a1=5×2+1,a2=5×3+2,a3=5×4+3,
a4=5×5+4,a5=5×6+5,…,当an=2021时,n的值为 .
18.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
三、解答题:本大题共9小题,共66分,解答应写出必要的文字说明、证明过程或演算步骤。
19.(5分)计算:.
20.(5分)先化简,再求值:,其中.
21.(7分)如图,在平行四边形中,对角线与交于点O,点M,N分别为、的中点,延长至点E,使,连接.
(1)求证:;
(2)若,试判断四边形的形状.
22.(6分) 如图,在平面直角坐标系中,反比例函数(x>0)的图象上有一点D(m,),过点D作CD⊥x轴于点C,将点C向左平移2个单位长度得到点B,过点B作y轴的平行线交反比例函数的图象于点A,AB=4.
(1)求反比例函数的解析式;
(2)设直线AD的解析式为y=ax+b(a,b为常数且a≠0).则不等式>0的解集为 .(直接填写结果)
23. (8分)甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款100 000元,乙公司共捐款140 000元,下面是甲、乙两公司员工的一段对话:
甲公司员工 乙公司员工
(1)甲、乙两公司各有多少人?
(2)现甲、乙两公司共同使用这笔捐款购买A、B两种防疫物资,A种防疫物资每箱15 000
元,B种防疫物资每箱12 000元.若购买B种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注:A、B两种防疫物资均需购买,并按整箱配送).
24.(8分)某校对九年级学生进行一次数学中考模拟测试,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90≤x≤100,B等级:80≤x<90,C等级:60≤x<80,D等级:0≤x<60.该校随机抽取了一部分学生的成绩进行调查,并绘制成如图不完整的统计图表.
请你根据统计图表提供的信息解答下列问题:
(1)上表中的a= ,b= ,m= .
(2)本次调查共抽取了多少名学生?请补全条形图.
(3)若从D等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.
25. (8分)如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,量得托板长,支撑板长,底座长,托板固定在支撑板顶端点处,且,托板可绕点转动,支撑板可绕点转动.(结果保留小数点后一位)
(1)若,,求点到直线的距离;
(2)为了观看舒适,在(1)的情况下,把绕点逆时针旋转后,再将绕点顺时针旋转,使点落在直线上即可,求旋转的角度.
(参考数据:,,,
,)
26.(8分)如图,在Rt△ABC中,∠ACB=90,以斜边AB上的中线CD为直径作⊙O,与BC交于点M,与AB的另一个交点为E,过M作MN⊥AB,垂足为N.
(1)求证:MN是⊙O的切线;
(2)若⊙O的直径为5,sinB=,求ED的长.
27.(11分)如图,在平面直角坐标系xOy中,直线y=kx+3分别交x轴、y轴于A,B两点,经过A,B两点的抛物线y=-x2+bx+c与x轴的正半轴相交于点C (1,0).
(1)求抛物线的解析式;
(2)若P为线段AB上一点,∠APO=∠ACB,求AP的长;
(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
九年级数学试卷参考答案
2022.6
一、选择题:本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的,不选,错选或多选均不得分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | C | A | A | C | A | C | B | B | D | B | D | B |
二、填空题:本大题共6小题,每小题3分,共18分。
13. . 14. 15. (4,1)或(-4,-1)
- 17. 336 . 18. .
三、解答题:本大题共9小题,共66分,
19.(5分)计算:.
【解】:原式=1﹣2+4+﹣1………………4分
=4﹣.…………………………1分
20.(5分)先化简,再求值:,其中.
【解】:原式
,………………………………3分
当时,原式.…………5分
- (7分)
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,ABCD,OA=OC,
∴∠BAC=∠DCA,
又点M,N分别为、的中点,
∴,
在和中,
,
∴.……3分
(2)BD=2BO,又已知BD=2AB,
∴BO=AB,∴△ABO为等腰三角形;
又M为AO的中点,
∴BM⊥AO,∴∠BMO=∠EMO=90°,
同理可证△DOC也为等腰三角形,
又N是OC的中点,
∴DN⊥CO,∴∠DNO=90°,
∵∠EMO+∠DNO=90°+90°=180°,
∴EMDN,
又已知EM=BM,由(1)中知BM=DN,
∴EM=DN,
∴四边形EMND为平行四边形,
又∠EMO=90°,∴四边形EMND为矩形。…………7分
22.(6分)
【解】:(1)D(m,),BC=2,∴OB=m﹣2,
又∵AB=4,AB⊥OC,∴A(m﹣2,4).……(2分)
反比例函数(x>0)的图象上有A,D两点,
∴k=4×(m﹣2)=m,解得m=3.
∴k=4,∴反比例函数的解析式为.…………(4分)
(2)0<x<1或x>3. …………………… (6分)
23.(8分)
【解】:(1)设乙公司有x人,则甲公司有(x- 30)人,由题意得
,解得x=180.
经检验,x=180是原方程的解.
x- 30= 150.
答:甲公司有150人,乙公司有180人.
(2)设购买A种防疫物资m箱,购买B种防疫物资n箱,由题意得
15000m+12000n = 100000 + 140000,整理得m=16-n.
又因为n≥10,且m,n为正整数,
所以。
答:有2种购买方案:购买8箱A种防疫物资、10箱B种防疫物资,或购买4箱A种防疫物资、15箱B种防疫物资.
24.(8分)
【解】:(1)a=8,b=12,m=30%;……3分
(2)本次调查共抽取了4÷10%=40名学生;
补全条形图如图所示;…………5分
(3)将男生分别标记为A,B,女生标记为a,b,
| A | B | a | b |
A |
| (A,B) | (A,a) | (A,b) |
B | (B,A) |
| (B,a) | (B,b) |
a | (a,A) | (a,B) |
| (a,b) |
b | (b,A) | (b,B) | (b,a) |
|
∵共有12种等可能的结果,恰为一男一女的有8种,
∴抽得恰好为“一男一女”的概率为:.………………8分
25(8分)
【解】(1)如图1,过点C作CH⊥DE于点H.
∵CD80,∠CDE=60°,∴sin60°=,
∴
作AM⊥DE于点M,CN⊥AM于点N.
∴MN=CH=,∠NCD=∠CDE=60°
∵∠DCB=80°,∴∠ACN=180°-80°-60°=40°.
∵sin∠ACN=∴AN=80sin40°≈80×0.643≈51.44.
∴AM=AN+NM≈51.44+69.28≈120.7mm.………………4分
(2)解法一:
∵AB绕着点C逆时针旋转10°,∴∠DCB=90°.
如图2,连接BD.
∵DC=80,CB=40.∴tan∠CDB==0.5.
∴∠CDB≈26.6°.∴∠BDE≈60°-26.6°=33.4°
答:CD旋转的度数约为33.4°………………8分
解法二:
当点B落在DE上时,如图3
在Rt△BCD中,BC=40,CD=80(∠DCB=90°,同解法一)
∴tan∠CDB==0.5.∴∠CDB≈26.6
∴∠=∠-∠BDC=60°-26.6°=33.4°
答:CD旋转的度数约为33.4°………………8分
26(8分)
(1)证明:连接OM,∵OC=OM,∴∠OCM=∠OMC.
在Rt△ABC中,CD是斜边AB上的中线,
∴CD=AB=BD,∴∠DCB=∠DBC,
∴∠OMC=∠DBC,∴OM∥BD
∵MN⊥BD,∴MN⊥OM,∴MN是⊙O的切线.………………4分
(2)解:连接DM,CE,易知DM⊥BC,CE⊥AB,
由(1)可知BD=CD=5,故M为BC的中点.
∵sinB=,∴cosB=,
在Rt△BMD中,BM= BD·cosB=4,∴BC=2BM=8
在Rt△CEB中,BE=BC·cosB=,∴ED=BE-BD=-5=.…………8分
说明:该题(1)(2)问均有多种方法,用其他合理方法得到正确结果都可给分.
27(11分)
【解】:(1)∵抛物线经过B(0,3),C(1,0),
∴
解得,
∴抛物线的解析式为y=﹣x2﹣2x+3.…………4分
(2)对于抛物线y=﹣x2﹣2x+3,令y=0,解得x=﹣3或1.
∴A(﹣3,0).
∵B(0,3),C(1,0),
∴OA=OB=3,OC=1,AB=3.
∵∠APO=∠ACB,∠PAO=∠CAB,
∴△PAO∽△CAB,
∴.
∴,
∴AP=2.……………………8分
(3)满足条件的点N的坐标为(﹣2,3)或(2,﹣5)或(﹣4,﹣5).………11分
初中学业水平考试数学模拟卷(四)含答案: 这是一份初中学业水平考试数学模拟卷(四)含答案,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中学业水平考试数学模拟卷(三)含答案: 这是一份初中学业水平考试数学模拟卷(三)含答案,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中学业水平考试数学模拟卷(二)含答案: 这是一份初中学业水平考试数学模拟卷(二)含答案,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












