2022-2023学年广西钦州市第四中学高一下学期3月月考数学试题含解析

2022-2023学年广西钦州市第四中学高一下学期3月月考数学试题

一、单选题

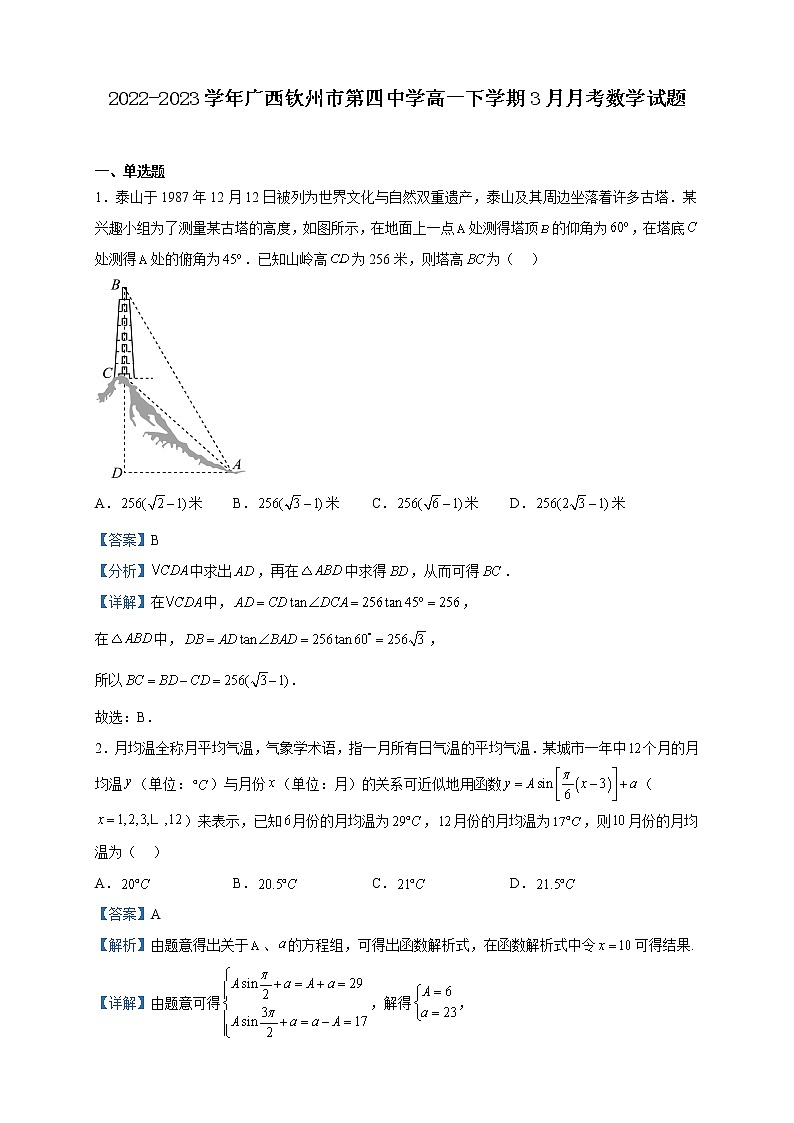
1．泰山于1987年12月12日被列为世界文化与自然双重遗产，泰山及其周边坐落着许多古塔．某兴趣小组为了测量某古塔的高度，如图所示，在地面上一点处测得塔顶的仰角为，在塔底处测得处的俯角为．已知山岭高为256米，则塔高为（    ）

A．米 B．米 C．米 D．米

【答案】B

【分析】中求出，再在中求得，从而可得．

【详解】在中，，

在中，，

所以．

故选：B．

2．月均温全称月平均气温，气象学术语，指一月所有日气温的平均气温．某城市一年中个月的月均温（单位：）与月份（单位：月）的关系可近似地用函数（）来表示，已知月份的月均温为，月份的月均温为，则月份的月均温为（    ）

A． B． C． D．

【答案】A

【解析】由题意得出关于、的方程组，可得出函数解析式，在函数解析式中令可得结果.

【详解】由题意可得，解得，

所以，函数解析式为，

在函数解析式中，令，可得.

因此，月份的月均温为.

故选：A.

3．的解集为（    ）

A． B．

C． D．

【答案】D

【分析】结合正切函数的图象求不等式在时的解集，再结合正切函数的周期性确定其解集.

【详解】作函数的图象，作函数的图象，

观察图象可得当时，，

即时，不等式的解集为，

又正切函数为周期函数，周期为，

所以不等式的解集为，

故选：D.

4．函数的定义域为（    ）

A． B．

C． D．

【答案】D

【分析】先根据对数函数定义域的求法得到，再利用三角不等式的解法求解.

【详解】若函数有意义，

则，

，

所以函数的定义域为.

故选：D

5．关于函数有下述四个结论，其中结论错误的是（    ）

A．的最小正周期为 B．的图象关于直线对称

C．的图象关于对称 D．在上单调递增

【答案】C

【分析】根据二倍角余弦公式、辅助角公式，结合正弦型函数的对称性、单调性、周期公式进行求解即可.

【详解】，

则的最小正周期为，故A正确；

因为，所以的图象关于直线对称，故B正确；

因为，

所以的图象不关于对称，故C不正确；

，所以在上单调递增，故D正确.

故选：C.

6．把函数的图象向左平移个单位长度，所得到的图象对应的函数是（    ）

A．奇函数 B．偶函数

C．既是奇函数也是偶函数 D．非奇非偶函数

【答案】A

【分析】根据诱导公式以及函数y＝Asin（ωx+φ）的图象变换规律可得所得的图象对应的函数为y＝＝sin2x，从而得出结论．

【详解】把函数的图象向左平移，所得的图象对应的函数为y＝sin[2（x）]＝sin2x的图象，

故所得函数为奇函数，

故选：A．

【点睛】本题主要考查诱导公式的应用，函数y＝Asin（ωx+φ）的图象变换规律，正弦函数的奇偶性，属于中档题．

7．要得到函数的图象，只需将函数的图象（    ）

A．向左平移个单位长度 B．向右平移个单位长度

C．向左平移个单位长度 D．向右平移个单位长度

【答案】B

【分析】根据三角函数平移变换原则直接判断即可.

【详解】，

只需将的图象向右平移个单位长度即可.

故选：B.

8．定义为中较大的数，已知函数，给出下列命题：

①为非奇非偶函数；

②的值域为；

③是以为最小正周期的周期函数；

④当时，.

其中正确的为（    ）

A．②④ B．①③ C．③④ D．①④

【答案】D

【分析】作出函数的图象，利用图象确定出奇偶性，值域，周期，单调区间，即可求解.

【详解】解：作出函数的图象，如下：

令，即，则，，解得，，

当，时，

由图可知，是非奇非偶函数，值域为，故①正确，②错误；

因为是以为最小正周期的周期函数，故③错误；

由图可知，时，，故④正确.

故选：D.

二、多选题

9．在函数①，②，③，④中，最小正周期为的所有函数为（    ）

A．① B．② C．③ D．④

【答案】ABC

【分析】对于①，根据与图象一致，由求出最小正周期；对于②，画出的图象，数形结合得到答案；对于③，利用求解；④利用求解.

【详解】对于①，本身为偶函数，故与图象一致，周期性也一致，

因为的最小正周期为，所以的最小正周期为，A正确；

对于②，的图象如下：

故的最小正周期为，B正确；

对于③，的最小正周期为，C正确；

对于④，的最小正周期为，D错误.

故选：ABC.

10．给出下列命题中，正确的是（    ）

A．存在实数，使

B．存在实数，使

C．函数是偶函数

D．若，是第一象限的角，且，则

【答案】BC

【分析】A由正弦的倍角公式直接判断；B由辅助角公式进行判断即可；C通过诱导公式及余弦函数的性质即可判断；D直接取特殊值判断即可.

【详解】对于，由，得，矛盾，错误；

对于，由，得，即成立，正确；

对于，，显然是偶函数，正确；

对于，取，，，是第一象限的角，且，但，错误．

故选：BC．

11．下列结论正确的是（   ）

A．是第三象限角 B．若圆心角为的扇形的弧长为，则该扇形面积为

C．若角为锐角，则角为钝角 D．若角的终边过点，则

【答案】BD

【分析】将化为，即可判断是第二象限角，判断A；根据弧长以及扇形面积公式可判断B；举反例判断C；根据三角函数的定义可判断D.

【详解】因为，故是第二象限角，A错误；

圆心角为的扇形的弧长为，则扇形的半径为，

故扇形面积为，B正确；

若角为锐角，不妨取，则角为锐角，C错误；

角的终边过点，则,则，D正确，

故选：

12．下列命题中正确的是（    ）

A．若且则为第二象限角

B．

C．若则

D．若角的终边在第一象限，则的取值集合为

【答案】AD

【分析】根据三角函数值符号判断象限角得出A选项，根据诱导公式求解B选项，特殊值法确定C选项，根据角的终边再确定半角范围确定函数值符号解决D选项.

【详解】若则为第二或四象限角且则为第一或二象限角, 则为第二象限角,A选项正确;

,B选项错误；

可取,则,C选项错误;

角的终边在第一象限, 则角的终边在第一或三象限,

角的终边在第一象限,

角的终边在第三象限,D选项正确.

故选:AD.

三、填空题

13．若是第四象限角，且,__________．

【答案】

【分析】先由条件结合同角关系求出，再由诱导公式可得的值.

【详解】因为是第四象限角，所以，

所以，又，故在第四象限，

，

所以，

所以，

故答案为：

14．若角的始边是轴非负半轴，终边落在直线上，则______.

【答案】/

【分析】利用三角函数的定义求出的值，利用诱导公式、二倍角的余弦公式以及弦化切化简可得所求代数式的值.

【详解】由已知可得，所以，，

所以，.

故答案为：.

15．若扇形的圆心角为，半径为6，则该扇形的面积为__________．

【答案】

【分析】将圆心角转成弧度制，利用扇形面积公式即可算得

【详解】圆心角为，即，所以扇形的面积为.

故答案为：

16．给出下列个命题：

①若是第二象限角，则是第一或第三象限角

②若，则；

③与角终边相同角的集合是；

④将函数的图像向左平移个单位可得到函数的图像；

⑤若是周期为的函数，则的周期为，

其中正确的命题是__________写出所有正确命题的编号．

【答案】①②④

【分析】根据象限角范围可以判断①正确；对的奇偶性进行讨论结合诱导公式可以判断②正确；根据终边相同角的定义可以判断③错误；利用平移变换特征可以判断④正确；利用周期性质可以判断⑤错误.

【详解】①若是第二象限角，    即，

则，

当时，，此时是第一象限角；

当时，，此时是第三象限角；

故①正确；

②当时，

当时，，

故②正确；

③根据终边相同角的定义，，故③错误；

④将函数的图像向左平移个单位，可得到函数

的图像；故④正确；

⑤若是周期为，则的周期为，故⑤错误；

故答案为：①②④.

四、解答题

17．求与角终边相同的最小正角和最大负角，并指出角是第几象限角.

【答案】最小正角为，最大负角为，角是第四象限角

【分析】由可确定其为第四象限角，结合终边相同的角的表示法可确定最小正角和最大负角.

【详解】，

角是第四象限角，与角终边相同的角可以表示为，

当时，；当时，；

与角终边相同的最小正角为，最大负角为.

18．若角的终边上有一点，且.

（1）求的值；

（2）求的值.

【答案】（1）；（2）.

【分析】（1）根据三角函数的概念，由题中条件，列出方程组求解，即可得出结果；

（2）先将原式化简，再由三角函数的定义求出，进而可得出结果.

【详解】（1）点到原点的距离为，

根据三角函数的概念可得，解得，（舍去）.

（2）原式，

由（1）可得，，

所以原式.

【点睛】本题主要考查由三角函数的定义求参数，以及根据诱导公式化简求值，属于常考题型.

19．已知函数.

（Ⅰ）求函数的最小正周期；

（Ⅱ）求函数在上的单调递增区间；

（Ⅲ）若是函数的一个零点，求实数的值及函数在上的值域.

【答案】（Ⅰ）；（Ⅱ）；（Ⅲ）.

【解析】利用三角恒等变换公式化简函数解析式，（1）利用周期公式求解；（2）利用换元法或整体代换法求函数单调递增区间；（3）利用换元法求判断函数单调性，并求值域.

【详解】解：（Ⅰ）

，

；

（Ⅱ）法一：

令；则.

，的单调增区间为.

，解得.

函数在上的单调递增区间.

法二：

，

，

画数轴与所有区间取交集可知：.

函数在上的单调递增区间；

（Ⅲ）是函数的一个零点

.

解得：.

.

，，当单调递减区间为.

，解得

在区间上为减函数.

函数在上的单调递增区间，单调递减区间

，，.

函数在上的值域为.

【点睛】对于三角函数，求最小正周期和最值时可先把所给三角函数式化为y＝Asin(ωx＋φ)或y＝Acos(ω x＋φ)的形式，则最小正周期为，最大值为，最小值为；奇偶性的判断关键是解析式是否为y＝Asin ωx或y＝Acos ωx的形式．

20．已知角，（，）的顶点与原点重合，始边与轴的非负半轴重合，点，分别在角，的终边上.

(1)设函数，，求函数的值域；

(2)若点在角的终边上，且线段的长度为，求的面积.

【答案】(1)

(2)

【分析】（1）先由任意角三角函数的定义结合的取值范围确定的大小，再求的值域（2）先由任意角三角函数的定义结合的取值范围确定的大小，从而求出的大小，再利用余弦定理，求出的长度，确定出点在上的位置之后，即可求的面积

【详解】（1）∵的终边过点，∴，.

∵，∴.

则，

∵，∴，∴，∴，

即的值域是.

（2）∵的终边过点，

∴，.

∵，∴，∴.

由余弦定理可得，，

∴，解得.

∵，∴为的中点，

∴则的面积

21．已知函数部分图像如图所示.

(1)求和值；

(2)求函数在上的单调递增区间；

(3)设，已知函数在上存在零点，求实数最小值和最大值.

【答案】(1)，

(2)单调递增区间为，，

(3)最小值为，最大值为

【分析】（1）由图像观察周期，计算；由最大值求出；

（2）利用整体代换求出单增区间；

（3）先求出，转化为，在上有解.令，求出的值域，即可求出a.

【详解】（1）由图像可知：，所以，则，

又，，得，

又，所以.

（2）.

要求的增区间，只需，，

解得：，.

令，得，

因，则，

令，得，

令，得，

因，则，

所以在上的单调递增区间为，，.

（3），

则.

由函数在上存在零点，

则，在上有解，

令，由，则，即，

则，

所以，即，

故a最小值为，最大值为.