数学九年级上册第21章 二次函数与反比例函数21.4 二次函数的应用教学ppt课件

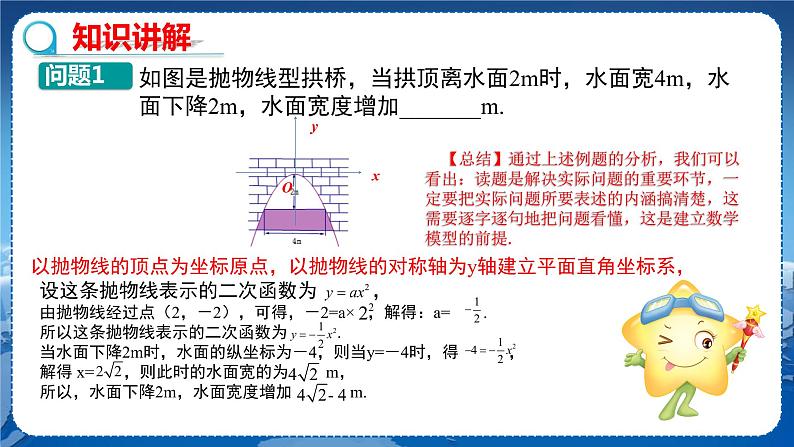
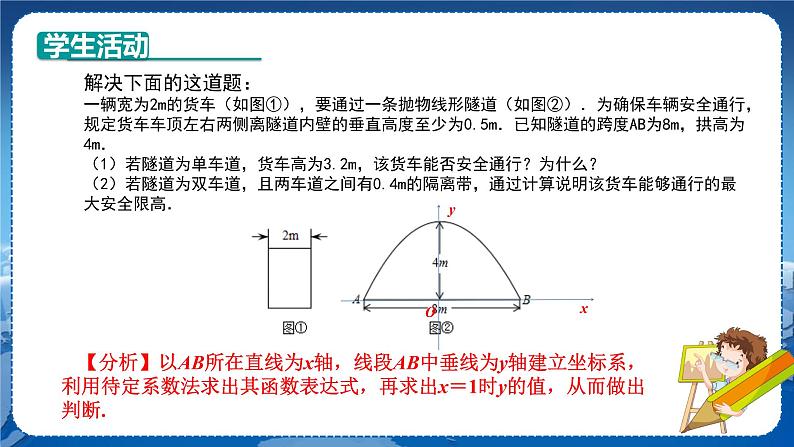
教学目标

1.熟练掌握二次函数模型的相关基础知识.

2.初步体会利用建模的思想解决实际问题的过程.

3.能够初步掌握建立函数模型解决实际问题的基本步骤.

教学重难点

重点：使学生初步掌握建立函数模型解决实际问题的基本步骤，体会建模的数学思想.

难点：建立函数模型解决实际问题.

教学过程

导入新课

【问题1】如图是抛物线形拱桥，当拱顶离水面2 m时，水面宽4 m，若水面下降2 m，则水面宽度增加            m.

探究新知

【活动】学生自主辨析：以抛物线的顶点为坐标原点，以抛物线的对称轴为y轴建立平面直角坐标系.设这条抛物线表示的二次函数为y＝ax2，由抛物线经过点(2，-2)，可得-2＝a×22，解得a＝，所以这条抛物线对应的函数表达式为.当水面下降2 m时，抛物线的纵坐标为-4，则当y＝-4时，得，解得x＝，则此时的水面宽度为m，所以水面下降2 m，水面宽度增加-4m.

【总结】1.通过上述例题的分析，我们可以看出：读题是解决实际问题的重要环节，一定要把实际问题所要表述的内容搞清楚，这需要逐字逐句地把问题看懂，这是建立数学模型的前提.

2.(引导学生通过题目归纳)解决抛物线型的建筑问题的关键：

合理建立平面直角坐标系，设出适当的二次函数表达式，利用待定系数法求出表达式，再由二次函数的性质解决问题.

【问题2】从房屋的窗户的形状如图所示，它的上半部分是四个小扇形组成的半圆，下半部分是由三个相同的小矩形组成，制作窗框的材料总长为15 m，设半圆的半径为x m，窗户的截面面积为S m2.

(1)求S与x之间的函数表达式，并求出x的取值范围；

(2)画出(1)中所求函数的图象；

(3)当x的长度为多少时，S有最大的值？最大的值是多少？(精确到0.01)

【思考】观察图形思考小矩形的宽与半圆的半径有什么关系？如何利用二次函数结合矩形面积公式列出函数表达式？

【互动】(引发学生思考，老师指导)试写出解题过程.

解：(1)设矩形的宽为y m，

∵材料的总长为15 m，

∴4y+7x+πx＝15，

∴y＝(15-7x-πx)，

从而S＝2x•(15-7x-πx)+＝-3.5x2+7.5x，

即S＝-3.5x2+7.5x.

(2)由(1)知S＝-3.5x2+7.5x＝-0.5x(7x-1.5)＝ ，

则函数图象与x轴的两个交点坐标是(0，0)，(1.5，0)，顶点坐标是，开口向下，其大致图象如图所示.

(3)如图所示，当x＝≈1.07时，S最大值＝≈4.02.

答：当x约为1.07 m时，S有最大值，此时S的最大值约为4.02 m2.

【问题3】下面让你们来解决下面的这道题：

一辆宽为2 m的货车(如图(1))，要通过一条抛物线形隧道(如图(2)).

为确保车辆安全通行，规定货车车顶左右两侧离隧道内壁的垂直高度至少为

0.5 m.已知隧道的跨度AB为8 m，拱高为4 m.

(1)若隧道为单车道，货车高为3.2 m，该货车能否安全通行？为什么？

(2)若隧道为双车道，且两车道之间有0.4 m的隔离带，通过计算说明该货车能够通行的最大安全限高.

(1) 　　　　　　　　　　　　(2)

【互动】(引导学生分析题目中的信息，结合图形和已知条件能确定出哪些量，让学生发现如何引入二次函数解决问题)

以AB所在直线为x轴，线段AB中垂线为y轴建立坐标系，利用待定系数法求出其函数表达式，再求出x＝1时y的值，从而做出判断.

【解题过程】(1)货车能安全通行.理由如下：

设抛物线对应的函数表达式为y＝ax2+4，

将B(4，0)代入，得16a+4＝0，

解得a＝-，

∴ 抛物线对应的函数表达式为.

由x＝1，可得y＝3.75.

∵ 3.75-0.5＝3.25＞3.2，

∴ 货车能够安全通行.

(2) ∵ 两车道之间有0.4 m的隔离带，∴ 由，可得y＝2.79.

∵ 2.79-0.5＝2.29（m），

∴ 货车能够通行的最大安全限高为2.29 m.

【总结】

1.同学们在解决问题时应选择适当的函数模型；

2.在解题时，能够直接弄清函数形式的可直接利用所给的函数关系求解，若并不能直接确定函数关系的，则应按照题目指明的相等关系建立函数模型，再进行求解.

课堂练习

1.某广场有一个小型喷泉，水流从垂直于地面的水管OA喷出，OA长为1.5 m.水流在各个方向上沿形状相同的抛物线路径落到地面上，某方向上抛物线路径的形状如图所示，落点B到O的距离为3 m.如图（2），建立平面直角坐标系，水流喷出的高度y(m)与水平距离x(m)之间近似满足函数表达式y＝ax2+x+c(a≠0)，则水流喷出的最大高度为(　　)

(1)　　　　　　　　　　　　(2)

A.1 m B. m C.2 m D. m

2.如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20 m，如果水位上升3 m达到警戒水位时，水面CD的宽是10 m.如果水位以0.25 m/h的速度上涨，那么达到警戒水位后，再过　   　h水位达到桥拱最高点O.

3.廊桥是我国古老的文化遗产，下图是某座抛物线形的廊桥示意图.已知水面AB宽40米，抛物线最高点C到水面AB的距离为10米，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，求这两盏灯的水平距离EF.(结果保留根号)

参考答案

1.C   2.4

3.解：如图，以AB所在直线为x轴、线段AB的中垂线为y轴建立平面直角坐标系.

由题意知，A(-20，0)，B(20，0)，C(0，10).

设过点A，B，C的抛物线对应的函数表达式为y＝a(x+20)(x-20)(a＜0).

把点C(0，10)的坐标代入，得

10＝a(0+20)(0-20)，

解得a＝-，

则该抛物线对应的函数表达式为y＝-(x+20)(x-20)＝-x2+10.

把y＝8代入，得-x2+10＝8，

解得x1＝4，x2＝-4.

所以两盏警示灯之间的水平距离为

EF＝|x1-x2|＝|4-(-4)|＝8(m).

课堂小结

1.本节课的重点是了解数学建模的基本步骤，体会数学建模的基本思想.

2.建立函数模型解决实际问题的步骤:

(1)认知读题、审清题意.

(2)设有关符号表示题目中的有关量.

(3)若已知题目中的函数关系，则直接利用函数的观点解题；若未知题目的函数关系，则根据题目中的等量关系用相关的符号来建立函数关系，并用函数的观点解答问题.

布置作业

某种电缆在空中架设时，两端挂起的电缆下垂都近似抛物线y＝ x2的形状，今在一个坡度为1∶5的斜坡BD上，沿水平距离间隔50米架设两个固定电缆位置的塔柱AB，CD，塔柱高度均为20米(如图)，以点B为原点，BE方向为x轴，AB所在直线为y轴，建立平面直角坐标系，解决下列问题：

(1)求电缆(AC段)所在抛物线对应的函数表达式；

(2)求下垂的电缆与斜坡BD的最近距离.

【答案】解：(1)由题意设抛物线对应的函数表达式为y＝x2+bx+c，

易知A(0，20)，C(50，30)，

代入，得

解得

∴抛物线对应的函数表达式为y＝x2-x+20.

(2)∵斜坡的坡度为1∶5，

∴斜坡所在直线对应的函数表达式为y＝x.

设一条与x轴垂直的直线x＝m与抛物线交于点M，与斜坡交于点G，

则MG＝m2-m+20-m＝(m-25)2+13.75，

∴当m＝25时，MG有最小值，最小值为13.75，

即下垂的电缆与地面的最近距离为13.75米.

板书设计

【问题1】

【问题2】                 

解决抛物线型的建筑问题的关键：

合理建立平面直角坐标系，设出适当的二次函数表达式，再利用待定系数法求出表达式，并由二次函数的性质解决问题.

教学反思

教学反思

教学反思

教学反思

教学反思

教学反思