北师大版八年级上册1 平均数完美版ppt课件

这是一份北师大版八年级上册1 平均数完美版ppt课件，文件包含611平均数教学课件教学课件pptx、62平均数第1课时学案+练习docx、第六章数据的分析61平均数第1课时教学详案docx等3份课件配套教学资源，其中PPT共18页， 欢迎下载使用。

1.掌握算术平均数、加权平均数的概念，会求一组数据的平均数和加权平均数.（重点）2.体会算术平均数和加权平均数的联系和区别.（难点）
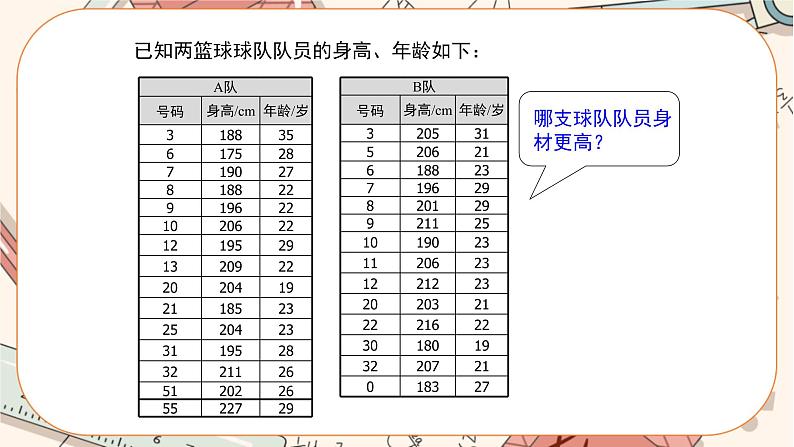
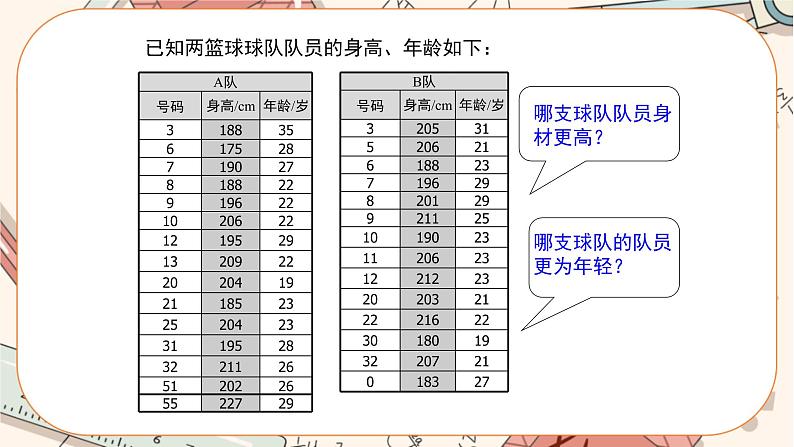
在篮球比赛中，影响比赛的成绩有哪些因素？ 如何衡量两个球队队员的身高？ 怎样理解“甲队队员的身高比乙队更高”？ 要比较两个球队队员的身高，需要收集哪些数据呢？
已知两篮球球队队员的身高、年龄如下：
上述两支篮球队中，哪支球队队员的身高更高？哪支球队的队员更为年轻？你是怎样判断的？与同伴交流。
在日常生活中，我们常用平均数描述一组数据的集中趋势。
一般地，对于n个数x1 ，x2 ，… ，xn ，我们把
小明是这样计算A队队员的年龄情况的：
平均年龄=（19×1＋22×4＋23 × 2＋ 26 × 2 ＋27 ×1 ＋28 × 2＋29 ×2+35 ×1 ） ÷（1＋4 +2＋2 ＋ 1＋2 ＋ 2 ＋ 1）
你能说说小明这样做的道理吗？
如果在n个数中，x1出现f1次，x2出现f2次，…，xk出现fk次（这里f1+f2+… +fk=n），那么
当一组数据中有若干个数据多次重复出现时，可以考虑下面的做法：
（1）如果根据三项测试的平均成绩决定录用人选，那么谁将被录用？ （2）根据实际需要，公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩，此时谁将被录用？
例 某广告公司欲招聘广告策划人员一名，对A,B,C三名候选人进行了三项素质测试，他们的各项测试成绩如下表所示：
（1）如果根据三项测试的平均成绩决定录用人选，那么谁将被录用？
解：（1）A的平均成绩为（72+50+88）÷3=70分。 B的平均成绩为（85+74+45）÷3=68分。 C的平均成绩为（67+70+67）÷3=68分。 由70>68，故A将被录用。
（2）根据实际需要，公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩，此时谁将被录用？
解∶（2）A的测试成绩为∶（72×4+50×3+88×1）÷（4+3+1）=65.75分。 B的测试成绩为∶（85×4+74×3+45×1）÷（4+3+1）=75.875分。 C的测试成绩为∶（67×4+70×3+67×1）÷（4+3+1）=68.125分。 因此候选人B将被录用。
思考：(1)(2)的结果不一样说明了什么？
某校规定学生的体育成绩由三部分组成:早锻炼及体育课外活动表现占成绩的20%,体育理论测试占30%,体育技能测试占50%,小颖的上述三项成绩依次是92分、80分、84分，则小颖这学期的体育成绩是多少？
解：小颖这学期的体育成绩是92×20%+80×30%+84×50%=84.4（分）
答:小颖这学期的体育成绩是84.4分
1、一组数据:40、37、x、64的平均数是53，则x的值是 （ ） A、67 B、69 C、71 D、722、甲、乙、丙三种饼干售价分别为3元、4元、5元，若将甲种7斤、乙种8斤、丙种10斤混到一起，则售价应该定为每斤 （ ） A、4.12元 B、5.13元 C、8.6元 D、10.8元3、某次考试A、B、C、D、E五名学生平均分为62分，除A以外四人平均分为60分，则A得分为 （ ）A、60 B、62 C、70 D、无法确定