初中数学第二章 相交线与平行线1 两条直线的位置关系优秀课件ppt

这是一份初中数学第二章 相交线与平行线1 两条直线的位置关系优秀课件ppt，共27页。PPT课件主要包含了情景引入，探究新知，相交线平行线概念，归纳总结，针对训练，两直线相交，∠1和∠3，位置关系，∠2和∠4，有公共顶点等内容，欢迎下载使用。

生活中处处可见建筑物、道路、桥梁、山川等。在大自然的杰作和人类的创造物中，蕴含着无数的相交线和平行线。
观察下面几幅图片，思考：在同一平面内，两条直线的位置关系有几种？
在同一平面内，两条直线的位置关系有______和______两种.
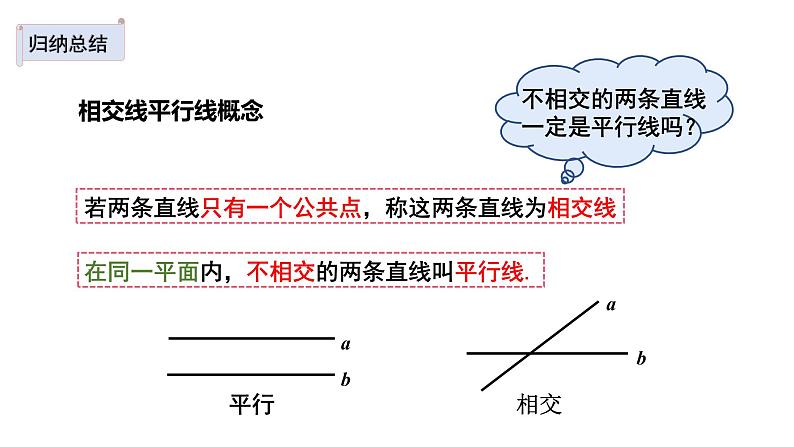
若两条直线只有一个公共点，称这两条直线为相交线
在同一平面内，不相交的两条直线叫平行线.
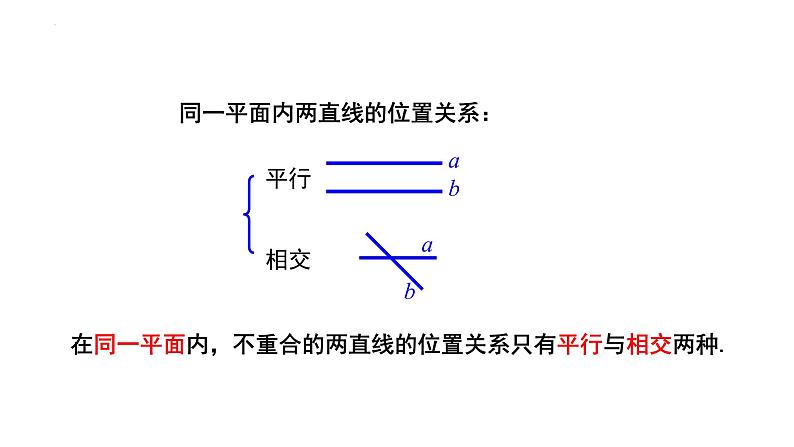
同一平面内两直线的位置关系：
在同一平面内，不重合的两直线的位置关系只有平行与相交两种.
注意：平行线的定义包含三层意思：（1）“在同一平面内”是前提条件；（2）“不相交”就是说两条直线没有交点；（3）平行线指的是“两条直线”而不是两条射线或两条线段．
练一练：下列说法中，正确的个数有（　　 ）（1）在同一平面内不相交的两条线段必平行（2）在同一平面内不相交的两条直线必平行（3）在同一平面内不平行的两条线段必相交 （4）在同一平面内不平行的两条直线必相交 A．1个 B．2个 C．3个 D．4个
如图，把两根木条用钉子钉在一起，转动其中一根木条，观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗?
∠1，∠2，∠3，∠4
两条直线相交，形成的小于平角的角有哪几个？
将这些角两两相配能得到几对角？
你能根据这几对角的位置关系，对它们进行分类吗？
3.两边互为反向延长线
图中的对顶角有:_________、_________.
如图，直线AB与CD相交于点O，∠1与∠3有____________，它们的两边________________，具有这种位置关系的两个角叫做________.
特别关注：（1）对顶角只有在两条直线相交时才出现． （2）对顶角是指两个角的位置关系．
练一练：下列各组角中，∠1与∠2是对顶角的为 ( )
探究：∠1 与∠3在数量上又有什么关系呢？
讨论：你能利用有关知识来验证∠1与∠3的数量关系吗？
已知：直线AB与CD相交于O点(如图),求证:∠1=∠3， ∠2=∠4.
证明：因为直线AB与CD相交于O点,
所以∠1+∠2=180° ∠2+∠3=180°，
符号语言：因为直线AB与CD相交于O点， 所以∠1=∠3，∠2=∠4.
如果两个角的和是90°，那么称这两个角互为余角.注：两个角不一定有公共边.
用手中的三角板，画一个直角三角形，如图1.
则∠A+∠B=_____.
如果两个角的和是90°，那么称这两个角互为_______.
如果两个角的和是180°，那么称这两个角互为补角.注：两个角不一定有公共边.
观察可得结论： 同一个锐角的补角比它的余角大________.
如图，已知：直线AB与CD交于点O， ∠EOD=90°.回答下列问题：（1）∠AOE的余角是_______________，补角是______；（2）∠AOC的余角是______，补角是______， 对顶角是_______.
打台球时，选择适当的方向，用白球击打红球，反弹后的红球会直接入袋，此时∠1=∠2，将图1抽象成图2，ON与DC交于点O，∠DON=∠CON=900，∠1=∠2.
观察思考，在图2中，解决下列问题：1.哪些角互为补角？哪些角互为余角？2.∠3与∠4有什么关系？为什么？3.∠AOC与∠BOD有什么关系？为什么？
解：(1)∠1与∠ AOC, ∠2与∠ BOD互补; ∠1与∠ 3, ∠2与∠ 4互余；
（2）因为∠1= ∠2，∠ 1+∠3=90° , ∠ 2+∠4=90°，所以 ∠ 3=∠4.
同角(等角)的余角相等
（3）因为∠1= ∠2，∠1+∠AOC=180°, ∠ 2+∠BOD=180°，所以∠AOC=∠BOD.
同角(等角)的补角相等
互余与互补只与角的数值有关，与位置无关。而对顶角是根据角的位置来判断的
有公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，这样的两个角，互为对顶角．对顶角相等.
如果两个角的和是90°，那么称这两个角互为余角.
如果两个角的和是180°，那么称这两个角互为补角.
1．如图，下列各组角中，互为对顶角的是（　　）
A．∠1和∠2B．∠1和∠3C．∠2和∠4D．∠2和∠5
2.下列说法中，正确的有（　 ） ①对顶角相等 ②相等的角是对顶角 ③不是对顶角的两个角就不相等 ④不相等的角不是对顶角 A．1个 B．2个 C．3个 D．0个
3.如图已知：直线AB与CD交于点O, ∠EOD=900, 回答下列问题： （1）∠AOE的余角是 ；补角是 ； （2）∠AOC的余角是 ；补角是 ； 对顶角是 ；