

小学数学人教版六年级下册2 正比例和反比例综合与测试巩固练习
展开
【单元专题卷】人教版数学6年级下册
第4章 专题02 正比例和反比例
一、选择题(共19小题)
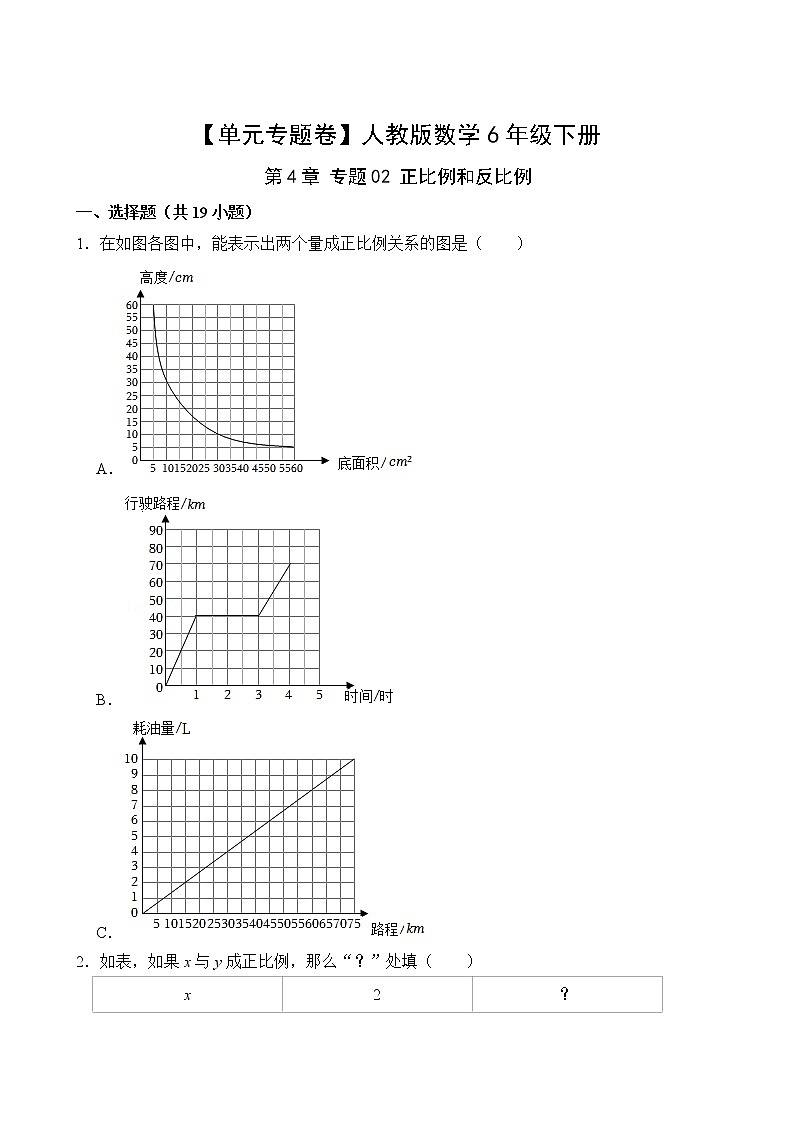
1.在如图各图中,能表示出两个量成正比例关系的图是( )
A.
B.
C.
2.如表,如果x与y成正比例,那么“?”处填( )
x | 2 | ? |
y | 8 | 24 |
A.8 B.3 C.6 D.0.5
3.下面图( )表示的是成正比例关系的图像。
A.
B.
C.
4.如图表示两辆汽车所行驶的路程与相应时间关系的图象,下列关于图象描述错误的是( )
A.两辆汽车行驶的路程和时间都成正比例
B.从昆明到大理大约有350千米,甲车从昆明到大理大约要4个小时
C.从图象上看甲车的速度比乙车快
D.从图象上看乙车的速度比甲车快
5.甲与乙是成反比例的量,如果甲增加25%,乙就会( )
A.增加25% B.减少25% C.增加20% D.减少20%
6.下面各题中,成反比例关系的是( )
A.路程一定,速度和时间 B.时间一定,路程和速度
C.单价一定,总价和数量 D.数量一定,总价和单价
7.下列两个量之间成正比例关系的是( )
A.如果y,x和y
B.同一个圆的周长和直径
C.积(0除外)一定,一个因数和另一个因数
D.一本书的总页数一定,已读的页数和未读的页数
8.若x和y都不为0,则表示x和y成正比例的式子是( )
A.x+y=3 B.xy=40 C.xy
9.如右表,当x和y成反比例时,m是( )
x | 5 | m |
y | 4 | 12 |
A.15 B.10 C.
10.表示x与y(x、y都不为0)成正比例关系的式子是( )
A.6x+5=y B.x﹣y=4 C.2x D.3x=y
11.成反比例的量是( )
A.A和B互为倒数
B.圆柱的高一定,体积和底面积
C.被减数一定,减数与差
D.除数一定,商和被除数
12.被减数一定,减数与差( )
A.成正比例 B.成反比例 C.不成比例
13.圆柱的体积一定,底面积和高( )
A.成正比例 B.成反比例 C.不成比例
14.三角形的高一定,它的面积和底( )
A.成正比例 B.成反比例 C.不成比例 D.没有关系
15.表中,如果a和b成反比例关系,空格里应填( )
a | 4 | 6 |
b |
| 12 |
A.2 B.8 C.18 D.24
16.正比例图象是一条( )
A.直线 B.线段 C.射线
17.( )中的两个量不成正比例。
A.在同一个正方形中,正方形的周长和边长
B.一箱苹果,吃掉的个数和剩下的个数
C.长方体的底面积一定,高和体积
D.订阅某期刊的份数一定,单价和总钱数
18.下列各种关系中,成反比例关系的是( )
A.如果5x=8y,则x和y
B.铺地面积一定,每块砖的面积和用砖块数
C.在同时同地条件下,竹竿的长和它的影长
D.同学的年龄一定,他们的身高与体重
19.下列数量关系中,成正比例关系的是( )
A.总价一定,购买的数量和单价
B.正方形的面积和边长
C.一个人的身高和年龄
D.长方体的底面积一定,长方体的体积和高
二、填空题(共19小题)
20.如果x和y成正比例,如表中的“?”处应该填 ,如果x和y成反比例,如表中的“?”处应该填 。
x | 50 | ? |
Y | 40 | 20 |
21.如表,如果a和b成正比例,X为 。
a | 60 | X |
B | 15 | 50 |
22.举出一个生活中成反比例关系的例子 。
23.如表中,如果x和y成正比例,“?”处填 。
x | 4 | ? |
y | 12 | 24 |
24.x与y成正比例。将表补充完整。
x | 3 |
|
| 10 |
y | 1.8 |
| 1.2 |
|
25.在中,当x与y成正比例时,“?”处应填 ;当x与y成反比例时,“?”处应填 。
26.下表中,若x与y成正比例关系,则★等于 ;若x与y成反比例关系,则★等于 .
x | 6 | 15 |
y | ★ | 4 |
27.下表中,如果x和y成正比例,“?”处应填 ;如果x和y成反比例,“?”处应填 。
x | 9 | ? |
y | 40 | 80 |
28.已知下面表格中x与y成反比例关系,那么表中的a= 。
X | 1.2 | 0.6 |
y | 4 | a |
29.表中,如果x与y成正比例,那么☆表示的数是 ;如果x与y成反比例,那么☆表示的数是 。
x | 3 | ☆ |
y | 4 | 24 |
30.x、y的对应值如表。若x与y成正比例关系,则m= ;若x与y成反比例关系,则m= 。
x | 4 | 6 |
y | 16 | m |
31.下面表格中,如果a和b成反比例,那么空格中应该填 ;如果a和b成正比例,那么空格中应该填 。
a | 5 | 8 |
b | 0.4 |
|
32.表中,A和B表示两个相关联的量。如果A与B成正比例,则☆是 ;如果A与B成反比例,则☆是 。
A | 10 | 15 |
B | 8 | ☆ |
33.如表,如果a与b成正比例,那么“?”是 ;如果a与b成反比例,那么“?”是 。
a | 40% | 10 |
b |
| ? |
34.如表,如果x与y成正比例,那么“?”处应填 ;如果x与y成反比例,那么“?”处应填 。
x | 2 | 5 |
y | 40 | ? |
35.若ab,则a与b成 比例;若xy,则x与y成 比例。
36.若xy,那么x和y成 比例关系;若,那么x和y成 比例关系。
37.若x与y成正比例,则m= ,若x与y成反比例,则m= 。
X | 4 | 5 |
y | 16 | m |
38.已知x和y是成正比例的两个量,请把如表填写完整。
x | 0.8 | 0.5 |
|
| 10 |
y | 1.2 |
| 24 |
|
|
三、应用题(共5小题)
39.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 | 4 | 9 | 16 |
所需小正方形的数量/个 | 216 | 96 | 54 |
(1)每个小正方形的面积与所需小正方形的数量成 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
40.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t | 2.5 | 3 | 5 | 10 |
数量/辆 | 48 | 40 |
|
|
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
41.“六一”那天,芳芳和小朋友们一起骑车去动物园玩.下面的图象表示的是她骑车的路程和时间的关系.
(1)芳芳骑车行驶的路程和时间成正比例吗?为什么?
(2)看图估计,行2.5千米大约用多少分钟?
42.
时间/时 | 1 | 2 | 3 | 4 | 5 | 6 | … |
路程/千米 | 90 |
|
|
|
|
| … |
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
43.平行四边形的高是3cm,先填表,再根据表中的数据回答问题.
底/cm | 8 | 10 | 20 | 30 |
面积/cm2 | 24 |
|
| 90 |
(1)表中平行四边形的底和面积是 的量,平行四边形的 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
四、解答题(共3小题)
44.如图表示的是一种笔记本单价与数量的反比例图像,读图可知当能买4本的时候单价是 元。
45.在下表的空格中填写合适的数。
已知x与y成正比例关系。
x | 12 |
| 18 |
y |
| 4.5 | 6 |
46.仔细观察,补全如表并回答下列问题。
x | 6 | 18 | 24 |
| 75 |
|
y | 2 | 6 |
| 10 |
| 120 |
(1)仔细观察,补全表格。
(2)观察表格,x与y这两个量的 一定,x和y成 比例。
(3)如果x=2.4,那么y= ,如果y,x= 。
参考答案
一、选择题(共19小题)
1.C
2.C
3.B
4.D
5.D
6.A
7.B
8.C
9.C
10.D
11.A
12.C
13.B
14.A
15.C
16.A
17.B
18.B
19.D;
二、填空题(共19小题)
20.25;100
21.200
22.从家去学校上学,行走的平均速度与到校所用的时间成反比例
23.8
24.2;;6
25.8;4.5
26.1.6;10
27.18;4.5
28.8
29.18;0.5
30.24;
31.0.25;0.64
32.12;
33.40;
34.100;16
35.反;正
36.正;反
37.20;12.8
38.16;;;15;
三、应用题(共5小题)
39.解:(1)长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)设需要多x个小正方形。
36x=216×4
36x÷36=216×4÷36
x=24
答:(1)每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)需要24个小正方形。
故答案为:反,24。
40.解:3×40÷5
=120÷5
=24(辆)
3×40÷10
=120÷10
=12(辆)
载质量/t | 2.5 | 3 | 5 | 10 |
数量/辆 | 48 | 40 | 24 | 12 |
(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,
所以车辆的载重量与所需车辆的数量成反比例.
(2)120÷6=20(辆)
答:用载重量6吨的卡车来运,一共需要20辆.
(3)120÷15=8(吨)
答:每辆卡车运8吨.
故答案为:24;12.
41.解:(1)芳芳骑车行驶的路程和时间成正比例,因为速度一定,路程与时间成正比例关系;
(2)利用图象估计,芳芳行2.5千米时大约用了15分钟.
42.解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时 | 1 | 2 | 3 | 4 | 5 | 6 | … |
路程/千米 | 90 | 180 | 270 | 360 | 450 | 540 | … |
②时间和路程成 正比例,理由是 路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行 225千米,行675千米需要 7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
43.解:10×3=30;20×3=60.
底/cm | 8 | 10 | 20 | 30 |
面积/cm2 | 24 | 30 | 60 | 90 |
(1)表中平行四边形的底和面积是相关联的量,平行四边形的面积随着底的变化而变化.
(2)3;3;3;3.比值大小相等,是个定值3.
(3)高,比值表示的意义是平行四边形的高.
(4)相关联的两种量成正比例.
由(2)可知3(一定),是比值一定,所以成正比例.
四、解答题(共3小题)
44.解:如图:
表示的是一种笔记本单价与数量的反比例图像,读图可知当能买4本的时候单价是30元。
故答案为:30。
45.解:12:y=18:6
18y=12×6
18y÷18=72÷18
y=4
x:4.5=18:6
6x=4.5×18
6x÷6=81÷6
x=13.5
x | 12 | 13.5 | 18 |
y | 4 | 4.5 | 6 |
故答案为:4,13.5。
46.解:(1)6:2=18:6=3
24÷3=8
10×3=30
75÷3=25
120×3=360
x | 6 | 18 | 24 | 30 | 75 | 360 |
y | 2 | 6 | 8 | 10 | 25 | 120 |
(2)x:y=3(一定),与y这两个量的比值一定,x和y成正比例。
(3)2.4÷3=0.8
3=2
答:如果x=2.4,那么y=0.8,如果y,x=2。
故答案为:8,30,25,360;比值,正;0.8,2。
小学数学人教版四年级下册平均数精品练习: 这是一份小学数学人教版四年级下册平均数精品练习,共8页。
小学数学人教版五年级下册异分母分数加、减法精品当堂达标检测题: 这是一份小学数学人教版五年级下册异分母分数加、减法精品当堂达标检测题,共7页。
人教版四年级下册平移优秀习题: 这是一份人教版四年级下册平移优秀习题,共10页。














