山东省济南市商河县2022-2023学年九年级上学期期末数学试题(含答案)

2022－2023学年第二学期九年级开学测试

数学试题

本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第I卷满分为40分；第Ⅱ卷满分为110分．本试题共6页，满分150分．考试时间为120分钟．

答卷前，请考生务必将自己的姓名、座号和准考证号填写在答题卡上，并同时将考点、姓名、准考证号和座号填写在试卷规定的位置上，考试结束后，将本试卷和答题卡一并交回。本考试不允许使用计算器．

第I卷（选择题  共40分）

一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1．如图所示，圆锥的俯视图是（    ）

A． B． C． D．

2．菱形，矩形，正方形都具有的性质是（    ）

A．四条边相等，四个角相等 B．对角线相等

C．对角线互相垂直  D．对角线互相平分

3．下列各点中，在函数图象上的是（    ）

A． B． C． D．

4．若关于x的一元二次方程有一个根为0，则a的值等于（    ）

A．－1 B．0 C．1 D．1或者－1

5．在一个不透明的盒子里，装有4个黑球和若干个白球，它们除颜色外没有任何其他区别，摇匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复，共摸球40次，其中10次摸到黑球，则估计盒子中大约有白球和黑球共（    ）

A．12个 B．16个 C．20个 D．30个

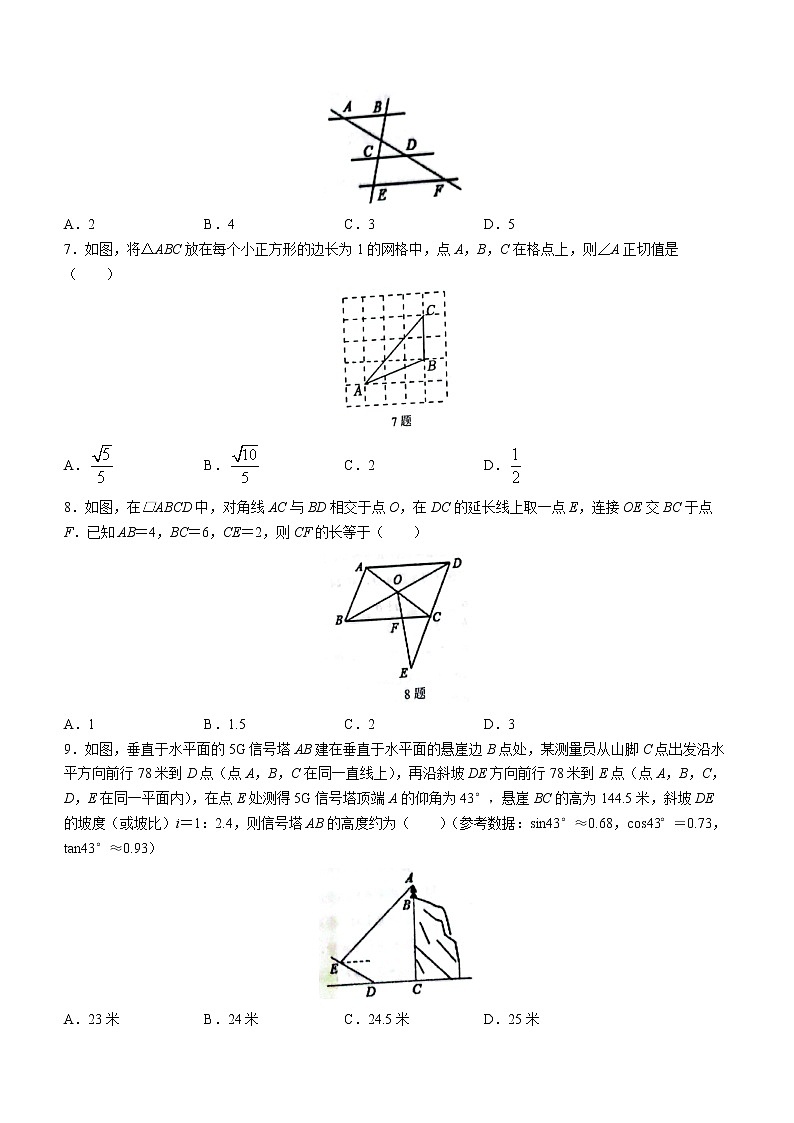
6．如图，已知，，BC＝6，CE的长为（    ）

A．2 B．4 C．3 D．5

7．如图，将△ABC放在每个小正方形的边长为1的网格中，点A，B，C在格点上，则∠A正切值是（    ）

A． B． C．2 D．

8．如图，在□ABCD中，对角线AC与BD相交于点O，在DC的延长线上取一点E，连接OE交BC于点F．已知AB＝4，BC＝6，CE＝2，则CF的长等于（    ）

A．1 B．1.5 C．2 D．3

9．如图，垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处，某测量员从山脚C点出发沿水平方向前行78米到D点（点A，B，C在同一直线上），再沿斜坡DE方向前行78米到E点（点A，B，C，D，E在同一平面内），在点E处测得5G信号塔顶端A的仰角为43°，悬崖BC的高为144.5米，斜坡DE的坡度（或坡比）i＝1：2.4，则信号塔AB的高度约为（    ）（参考数据：sin43°≈0.68，cos43°＝0.73，tan43°≈0.93）

A．23米 B．24米 C．24.5米 D．25米

10．已知，，抛物线顶点在线段AB上运动，形状保持不变，与x轴交于C，D两点（C在D的右侧），下列结论：

①；

②当时，一定有y随x的增大而增大；

③若点D横坐标的最小值为－5，则点C横坐标的最大值为3；

④当四边形ABCD为平行四边形时，．

其中正确的是（    ）

A．①③ B．②③ C．①④ D．①③④

第Ⅱ卷（非选择题  共110分）

二、填空题（每小题4分，共24分）

11．若，则______．

12．如图，在Rt△ABC中，∠BCA＝90°，D为AB的中点．若AB＝16，则CD＝______．

13．如果关于x的方程有两个相等的实数根，那么m＝______．

14．在测量旗杆高度的活动课中，某小组学生于同一时刻在阳光下对一根直立于平地的竹竿及其影长和旗杆的影长进行了测量，得到的数据如图所示，根据这些数据计算出旗杆的高度为______m．

15．如图所示，点B，A分别在反比例函数和的图象上，轴，点C在x轴的负半轴上，若，则的值为______．

16．如图，在边长为6的正方形ABCD中，点E是AB的中点，过点E作DE的垂线交正方形外角∠CBG的平分线于点F，交边BC于点M，连接DF交BC于点N，则MN的长为______．

三、解答题（本大题共10个小题，共86分．解答应写出文字说明，证明过程或演算步骤．

17．（本小题满分6分）解下列方程：

（1）  （2）

18．（本小题满分6分）计算：

（1） （2）

19．（本小题满分6分）已知二次函数．

（1）将二次函数的解析式化为的形式．

（2）二次函数图象的对称轴是直线______、顶点坐标是______．

20．（本小题满分8分）为巩固防疫成果，确保校园平安，全市所有学校都严格落实测体温进校园的防控要求，我校开设了A、B、C三个测温通道，某天早晨，该校小亮和小丽两位同学将随机通过测温通道进入校园．

（1）小亮从A测温通道通过的概率是______；

（2）利用画树状图或列表的方法，求小亮和小丽从同一个测温通道通过的概率．

21．（本小题满分8分）“一人一盔安全守规，一人一带平安常在”！某商店以每顶50元的价格购进一批头盔，售价为每顶80元时，每月可售出200顶，在“创建文明城市”期间，计划将头盔降价销售，经调查发现：每降价1元，每月可多售出20顶．该商店每月获得利润为7500元，求每顶头盔售价为多少元？

22．（本小题满分8分）如图，四边形ABCD是平行四边形，对角线AC，BD交于点O，，，．

（1）求证：四边形ABEO是菱形．

（2）若，BD＝8，求四边形ABEO的面积．

23．（本小题满分10分）已知△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC、CE、EG在同一直线上，且，BC＝1．连接BF，分别交AC、DC、DE于点P、Q、R．

（1）求证：△BFG∽△FEG；

（2）求出BF的长；

（3）求______（直接写出结果）．

24．（本小题满分10分）如图，在平面直角坐标系中，、是矩形OACB的两个顶点，双曲线经过AC的中点D，点E是矩形OACB与双曲线的另一个交点，

（1）点D的坐标为______，点E的坐标为______；

（2）动点P在第一象限内，且满足；

①若点P在这个反比例函数的图象上，求点P的坐标；

②若点Q是平面内一点，使得以A、C、P、Q为顶点的四边形是菱形，请你直接写出满足条件的所有点Q的坐标．

25．（本小题满分12分）在△ABC中，AB＝AC，，点P为线段CA延长线上一动点，连接PB，将线段PB绕点P逆时针旋转，旋转角为，得到线段PD，连接DB，DC．

（1）如图1，当时，填空：

①线段PA与DC的数量关系是______；②∠DCP的度数是______；

（2）如图2，当时，（1）中的结论还成立吗？若成立，请给出证明，不成立，说明理由；

（3）当时，若AB＝6，，请直接写出点D到CP的距离．

26．（本小题满分12分）如图，抛物线经过，两点，与y轴交于点B，P为抛物线上的动点，连接AB，BC，PA，PC，PC与AB相交于点Q．

（1）求抛物线的解析式；

（2）若P为第一象限抛物线上的动点，设△APQ的面积为，△BCQ的面积为，当时，求点P的坐标；

（3）是否存在点P，使，若存在，直接写出点P的坐标；若不存在，说明理由．

2022－2023期末考试九年级数学答案

一、选择题

（本大题共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只一项是符合题目要求的．）

二、填空题（本大题共6个小题，每小题4分，共24分．）

11．   12．8   13．9   14．12   15．6   16．

三．解答题（本大题共10个小题，共86分．解答题应写出文字说明、证明过程或演算步骤．）

17．（每小题3分，本题满分6分）

（1），－－－－－－－－－－－－－－－－－－－－－3分

（2），－－－－－－－－－－－－－－－－－－－－－－－6分

18．（每小题3分，本题满分6分）

（1）原式－－－－－－－－－－－－－－－－－－－－－－－－－－－3分

（2）原式－－－－－－－－－－－－－－－－－－－－－－－－－－－6分

19．（本题满分6分）

解：（1）；－－－－－－－－－－－－－－4分

（2）、．－－－－－－－－－－－－－－－－－－－－－－－－－－－6分

20．（本题满分8分）

解：（1）小亮从A测温通道通过的概率是，－－－－－－－－－－－－－－－－－－－－－－－2分

（2）列表如下：

由表可知，共有9种等可能的结果，其中小明和小丽从同一个测温通道通过的有3种可能，

所以小亮和小丽从同一个测温通道通过的概率为．－－－－－－－－－－－－－－－－－－－－8分

21．（本小题满分8分）

解：设每顶头盔售价为x元，

根据题意，得，

解得x＝65或x＝75，

答：每顶头盔售价为65或75元．

22．（本小题满分8分）

证明：（1）∵，，

∴四边形ABEO是平行四边形，

∵四边形ABCD是平行四边形，∴AC＝2AO，

∵AC＝2AB，∴AO＝AB，

∴四边形ABEO是菱形；－－－－－－－－－－－－－－－－－－－－－－4分

（2）解：∵四边形ABCD是平行四边形，

∴，，

连接AE交BO于M，

由（1）知，四边形ABEO是菱形，

∴AE、OB互相垂直平分，

∴，

∴，

∴AE＝8，

∴四边形ABEO的面积．－－－－－－－－－－－－－－－－－－－－－8分

23．（本小题满分10分）

（1）证明：∵△ABC、△DCE、△FEG是三个全等的等腰三角形，

∴，GE＝BC＝1，BG＝3BC＝3，

∴，，∴，

∵∠FGE＝∠BGF，∴△BFG∽△FEG；－－－－－－－－－－－－－－－－－－－－－－5分

（2）由（1）知：△BFG∽△FEG，

∴，∴

∵FG＝FE，∴BF＝BG＝3；－－－－－－－－－－－－－－－－－－－－－－8分

（3）．－－－－－－－－－－－－－－－－－－－－－－10分

24．（本小题满分10分）

解：（1），，－－－－－－－－－－－－－－－－－－－－－－2分

（2）①由题意知，

，

∵．∴，

∴，∴，

∴P的坐标为；－－－－－－－－－－－－－－－－－－－－－－6分

②点或或或－－－－－－－－－－－－－－－－－－－－－－10分

25．（本小题满分12分）

解：（1）①PA＝DC，②60°；－－－－－－－－－－－－－－－－－－－－－－4分

（2）如图1，

（1）中的结论不成立，理由如下：

∵AB＝AC，∠BAC＝120°，∴∠ABC＝∠ACB＝30°，

同理可得，∠PBD＝30°，

∴∠ABC＝∠PBD，∴∠ABC＋∠ABD＝∠PBD＋∠ABD，

即：∠CBD＝∠ABP，

∵，∴△CBD∽△ABP，

∴，∠BCD＝∠PEB＝180°－∠BAC＝60°，

∴∠PCD＝∠BCD－∠ACB＝60°－30°＝30°，

故：   ∠PCD＝30°，－－－－－－－－－－－－－－－－－－－－－8分

（3）点D到CP的距离为或．－－－－－－－－－－－－－－－－－－－－－12分

26．（本小题满分12分）解：（1）将，代入，

得，解得：，

∴抛物线的解析式为；－－－－－－－－－－－－－－－－－－－－－－4分

（2）∵，∴，

∵，，，∴，，

∴，∴，

设，∴，

∴t＝1或t＝2，∴或；－－－－－－－－－－－－－－－－－－－－－－8分

（3）点P的坐标为或．－－－－－－－－－－－－－－－－－－－－－－12分