山东省济南市长清区2022-2023学年九年级上学期期末数学试题

九年级阶段检测数学试题

注意事项：

本试题共8页，满分为150分，考试时间为120分钟.答卷前，请考生务必将自己的姓名、座号和准考证号填写在答题卡上，并将考点、姓名、准考证号和座号填写在试题规定的位置.考试结束后，仅交回答题卡.

第Ⅰ卷（选择题  共40分）

一、选择题（本大题共10小题，每小题4分，共40分.）

1.的值为（    ）

A. В. C. D.1

2.如图中几何体的左视图为（    ）

A.  B.

C.  D.

3.如果，那么下列比例式中正确的是（    ）

A. B. C. D.

4.下列的各点中，在反比例函数图象上的点是（    ）

A. B. C. D.

5.关于的一元二次方程有两个相等的实数根，则的值为（    ）

A. B. C.0 D.1

6.若点，，在反比例函数（）的图象上，则下列结论中正确的是（    ）

A. B. C. D.

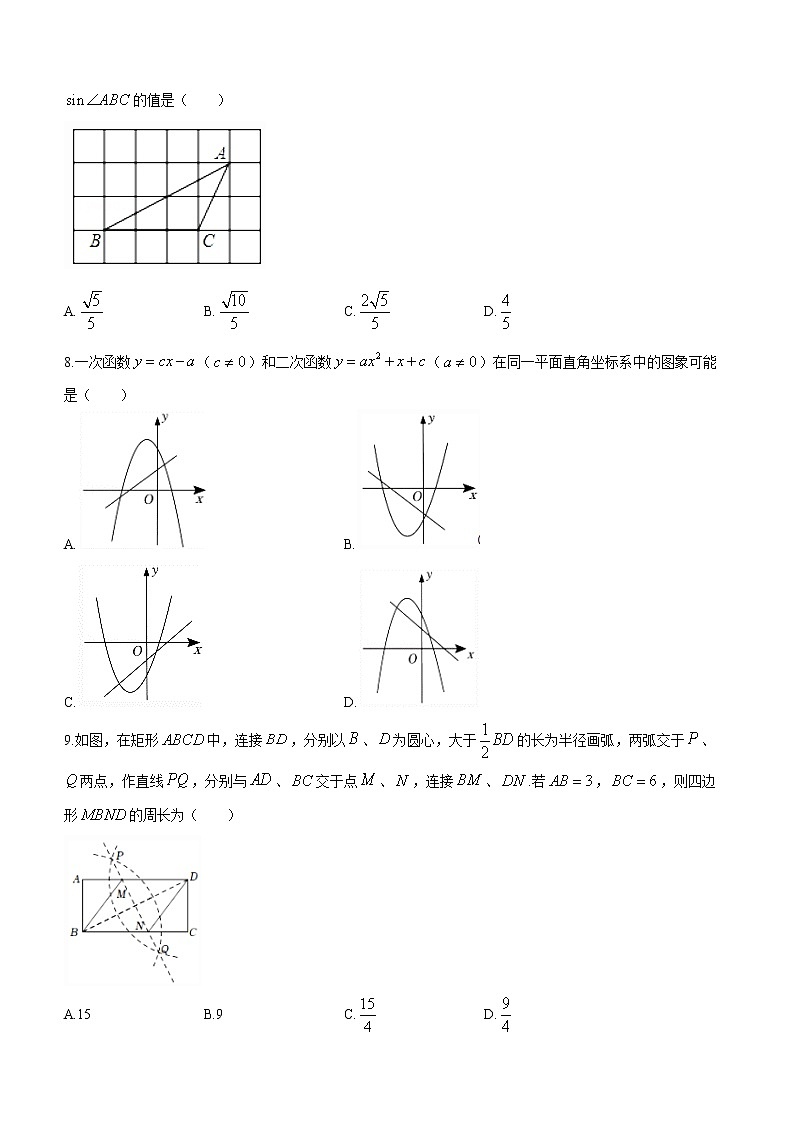
7.如图，在网格正方形中，每个小正方形的边长为1，顶点为格点，若的顶点均是格点，则的值是（    ）

A. B. C. D.

8.一次函数（）和二次函数（）在同一平面直角坐标系中的图象可能是（    ）

A. B.

C.  D.

9.如图，在矩形中，连接，分别以、为圆心，大于的长为半径画弧，两弧交于、两点，作直线，分别与、交于点、，连接、.若，，则四边形的周长为（    ）

A.15 B.9 C. D.

10.如图，已知开口向上的抛物线与轴交于点，对称轴为直线.下列结论：①；②；③若关于的方程一定有两个不相等的实数根；④.其中正确的个数有（    ）

A.1个 B.2个 C.3个 D.4个

二、填空题（本大题共6小题，每小题4分，共24分.）

11.如图，四边形四边形，若，，，则______°.

12.在一个不透明的袋子里装有若干个红球和6个黄球，这些球除颜色外都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则估计袋子中红球的个数是______个.

13.如图，若点在反比例函数（）的图象上，轴于点，的面积为8，______.

14.将抛物线向右移3单位，上移2单位所得到的新抛物线解析式为______.

15.定义一种运算：，.

例如：当，时，，

则的值为______.

16.如图，在正方形中，点、为边和上的动点（不含端点），，

下列四个结论：①当时，则；②；③的周长不变；④若，，则的面积为15.其中正确结论的序号是______.

三、解答题（本大题共10小题，共86分）

17.（6分）计算：.

18（6分）.

19.（6分）如图，在菱形中，于点，于点，求证：.

20.（8分）如图，，，，，.求的长度.

21.（8分）某校为落实“双减”工作，增强课后服务的吸引力，充分用好课后服务时间，为学有余力的学生拓展学习空间，成立了5个活动小组（每位学生只能参加一个活动小组）：.音乐；.体育；.美术；.阅读；.人工智能.为了解学生对以上活动的参与情况，随机抽取部分学生进行了调查统计，并根据统计结果，绘制了如图所示的两幅不完整的统计图.

根据图中信息，解答下列问题：

（1）①此次调查一共随机抽取了______名学生；

②补全条形统计图（要求在条形图上方注明人数）；

③扇形统计图中圆心角______度；

（2）若该校有2800名学生，估计该校参加组（阅读）的学生人数；

（3）学校计划从组（人工智能）的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛，请用树状图法或列表法求出恰好抽中甲、乙两人的概率.

22.（8分）为进一步加强疫情防控工作，长清区某学校决定安装红外线体温检测仪，对进入测温区域的人员进行快速测温（如图1），其红外线探测点可以在垂直于地面的支杆上下调节（如图2），已知探测最大角（）为61°，探测最小角（）为37°.若该校要求测温区域的宽度为1.4米，请你帮助学校确定该设备的安装高度.

（参考数据：，，，，）

23.（10分）某商店准备进一批季节性小家电，单价40元，经市场预测，销售定价为52元时，可售出180个.现在采取提高商品定价减少销售量的办法增加利润，定价每增加1元，销售量净减少10个.

（1）商店若将准备获利2000元，则定价应增加多少元？

（2）若商店要获得最大利润，则定价应增加多少元？最大利润是多少？

24.（10分）如图，一次函数的图象与反比例函数（）的图象交于点，与轴交于点.点在反比例函数（）的图象上的一点，轴，垂足为，与交于点，.

（1）求，的值；

（2）若点为轴上的一点，求当最小时，点的坐标；

（3）是平面内一点，是否存在点使得以、、、为顶点的四边形是平行四边形？若存在，请直接写出所有符合条件的点的坐标；若不存在，请说明理由.

25.（12分）【发现问题】

（1）如图1，已知和均为等边三角形，在上，在上，易得线段和的数量关系是______.

（2）将图1中的绕点旋转到图2的位置，直线和直线交于点.

①判断线段和的数量关系，并证明你的结论；

②图2中的度数是______.

【探究拓展】

（3）如图3，若和均为等腰直角三角形，，，，直线和直线交于点，分别写出的度数，线段、间的数量关系，并说明理由.

26.（12分）综合与探究：如图，抛物线（）与轴交于点和点，与轴交于点.

（1）求此抛物线的函数表达式；

（2）若点是第三象限抛物线上一动点，连接，，，求面积的最大值，并求出此时点的坐标；

（3）若点在抛物线的对称轴上，线段绕点逆时针旋转90°后，点的对应点恰好也落在此抛物线上，请直接写出点的坐标.

九年级阶段检测数学试题答案

一、选择题（本大题共10小题，每小题4分，共40分）

二、填空题（本大题共6小题，每小题4分，共24分.）

11. 115   12. 2   13.   14.   15.   16.①③.

三.解答题（本大题共10小题，共86分）

17.（6分）计算：

18.（6分）.

公式法：算出，，

因式分解法：，，

配方法：，，

19.（6分）

证明：菱形，，

，.

（或者连接，证）

.

20.（8分）

证明：，，

，

，，

21.（8分）

根据图中信息，解答下列问题：

（1）①400；②60，60；③54

（2）（人）

答：参加组（阅读）的学生人数为280人

（3）列表或画树状图正确

共有12中等可能的结果，其中恰好抽到，两人同时参赛的有两种

（恰好抽中甲、乙两人）

22.（8分）

方法1：解：在中，，

设，则

在中，，

.

经检验，是原方程的解

方法2：

解：在中，

设，则

在中，

经检验，是原方程的解

23.（10分）

（1）解：设定价应增加元

解得，

采取提高商品定价减少销售量的办法增加利润

不合题意舍去，

答：定价应增加8元.

（1）设定价增加元时获利元

当时，有最大值，为2250元.

答：若商店要获得最大利润，则定价应增加3元，最大利润是2250元.

24.（10分）

（1）求出，；

（2）求出，画图找到点，求出点的坐标；

（3），，

25.（12分）【发现问题】

（1）

（2）①，证明过程  ②60度

（3）写出度，证明过程

26.（12分）

（1）解出，，抛物线的函数表达式

（2）求出点，直线关系式

设点，过点作轴的垂线，交于点，

则点，

当时，S有最大值为，此时，

（3），