




北师大版九年级下册3 确定二次函数的表达式教课ppt课件
展开教学目标1.让学生利用已知条件设立恰当的函数表达式,用待定系数法求二次函数的表达式.2.指导学生利用二次函数的表达式和性质解决问题.
教学重点如何根据已知条件设定恰当的函数表达式.
教学难点 在实际问题中,体会二次函数作为一种数学模型的作用,会利用二次函数的性质求实际问题.
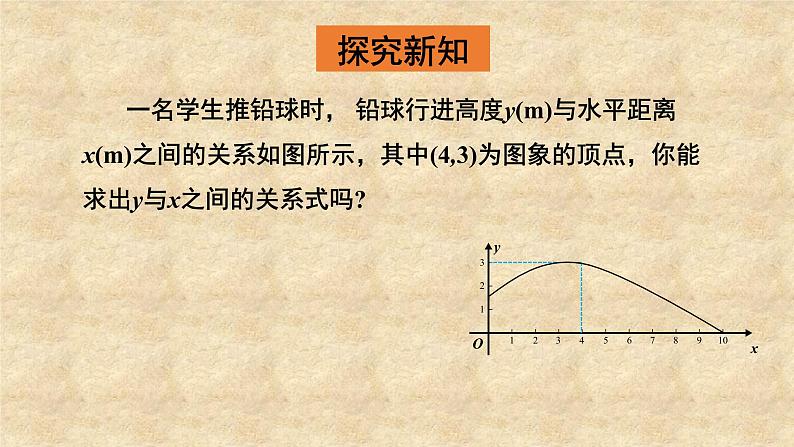
一名学生推铅球时, 铅球行进高度y(m)与水平距离x(m)之间的关系如图所示,其中(4,3)为图象的顶点,你能求出y与x之间的关系式吗?
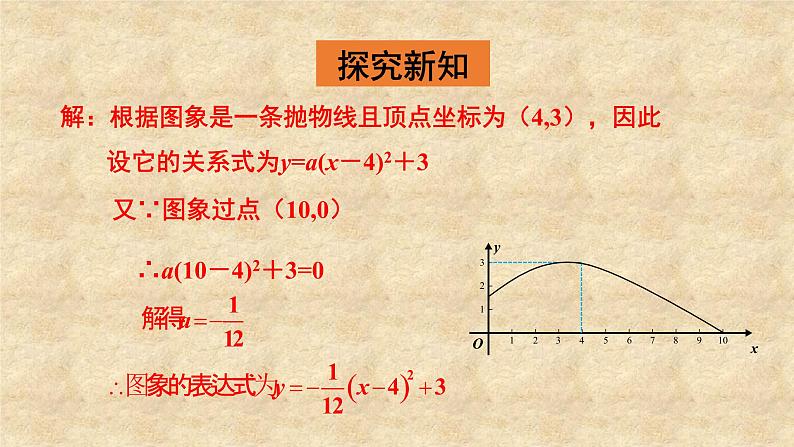
解:根据图象是一条抛物线且顶点坐标为(4,3),因此设它的关系式为y=a(x-4)2+3
又∵图象过点(10,0)
∴a(10-4)2+3=0
例1 已知二次函数y=ax2+c的图象经过点(2,3)和(-1,-3),求这个二次函数的表达式.
解:将点(2,3)和(-1,-3)的坐标分别带入表达式y=ax2+c,得
所以,所求二次函数表达式为y=2x2-5.
已知二次函数的图象与y轴交点的纵坐标为1,且经过点(2,5)和(-2,13),求这个二次函数的表达式.
解:因为抛物线与y轴交点纵坐标为1,所以可设抛物线关系式为y=ax2+bx+1,则可得:
13=4a-2b+1.
∴二次函数表达式为y=2x2-2x+1.
解:设二次函数的表达式为y=ax2+bx+c,由题意得
13=4a-2b+c.
1. 已知二次函数的顶点坐标是(-1,1),且经过点(1,-3),求这个二次函数的表达式.
解:根据题意,设二次函数的表达式为y=a(x-h)2+k
∵顶点坐标为(-1,1),
∴h=-1, k=1.
把点(1,-3)代入y=a(x+1)2+1得,
a(1+1)2+1=-3,
∴ 二次函数表达式为y= -(x+1)2+1.
2. (1)已知二次函数y=x²+bx+c的图象经过(1,1)与(2,3)两点,求这个二次函数的表达式;
解:由题意把(1,1)与(2,3)y=x2+bx+c得,
∴二次函数表达式为y=x2-x+1.
初中数学北师大版九年级下册3 确定二次函数的表达式教课课件ppt: 这是一份初中数学北师大版九年级下册3 确定二次函数的表达式教课课件ppt,共19页。PPT课件主要包含了复习导入,探究新知,a-b+c,a+b+c,4a+2b+c,解这个方程组得,b-3,议一议,a-1,a+b+1等内容,欢迎下载使用。
北师大版九年级下册3 确定二次函数的表达式一等奖习题课件ppt: 这是一份北师大版九年级下册3 确定二次函数的表达式一等奖习题课件ppt,文件包含232根据三个条件确定二次函数的表达式课件pptx、第二章二次函数3确定二次函数的表达式习题232课件pptx、232由三点确定二次函数的表达式教案doc等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
初中数学北师大版九年级下册3 确定二次函数的表达式获奖习题ppt课件: 这是一份初中数学北师大版九年级下册3 确定二次函数的表达式获奖习题ppt课件,文件包含231根据两个条件确定二次函数的表达式课件pptx、第二章二次函数3确定二次函数的表达式习题231课件pptx、231由两点确定二次函数的表达式教案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。













