专题02 倍长中线（解析版）

这是一份专题02 倍长中线（解析版），共27页。






















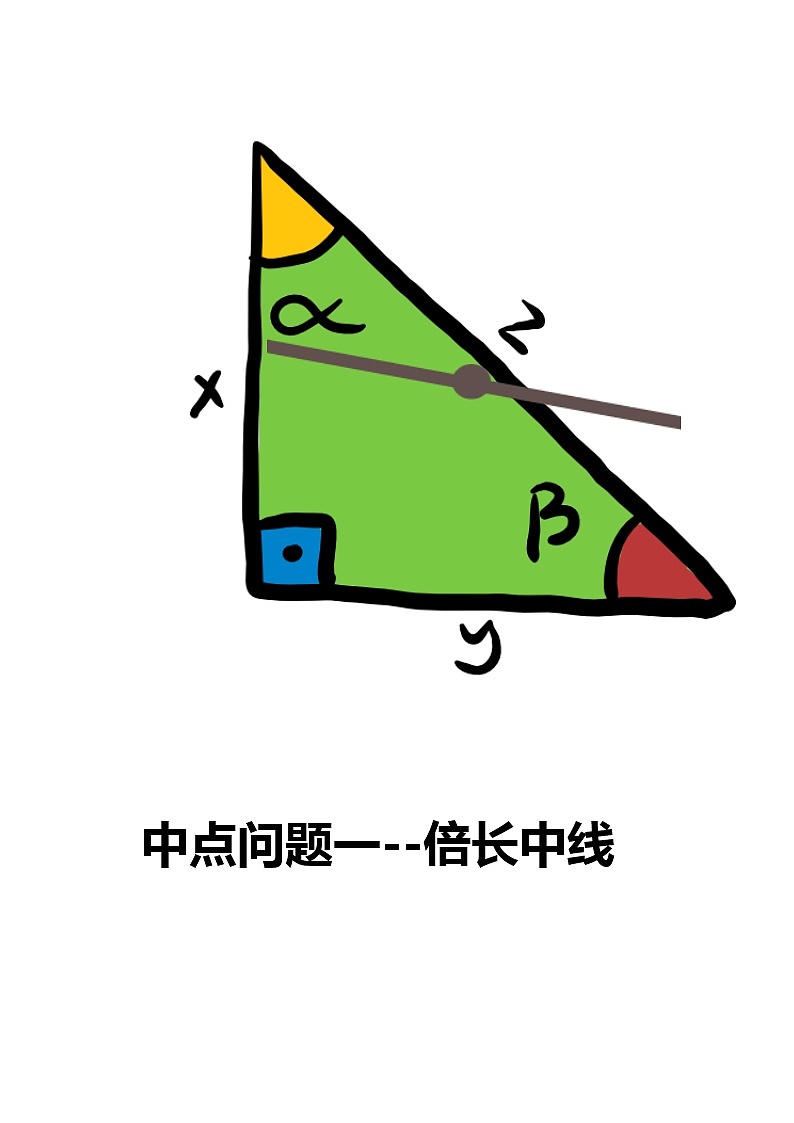
中点问题一--倍长中线







模型讲解



【模型一】
已知：在△ABC中，D为AC中点，连接BD并延长到E使得DE=BD，连接AE则：BC平行且等于AE．





【证明】：
延长BD到E，使DE＝BD，连接CE，
∵AD是斜边BC的中线
∴AD＝CD
∵∠ADE＝∠BDC
∴△ADE≌△BDC（SAS）
∴AE＝BC，∠DBC＝∠AED
∴AE∥BC
【模型二】
已知：在△ABC中，D为AC中点，连接BD并延长到E使得AE∥BC，连接AE则：BC=AE．







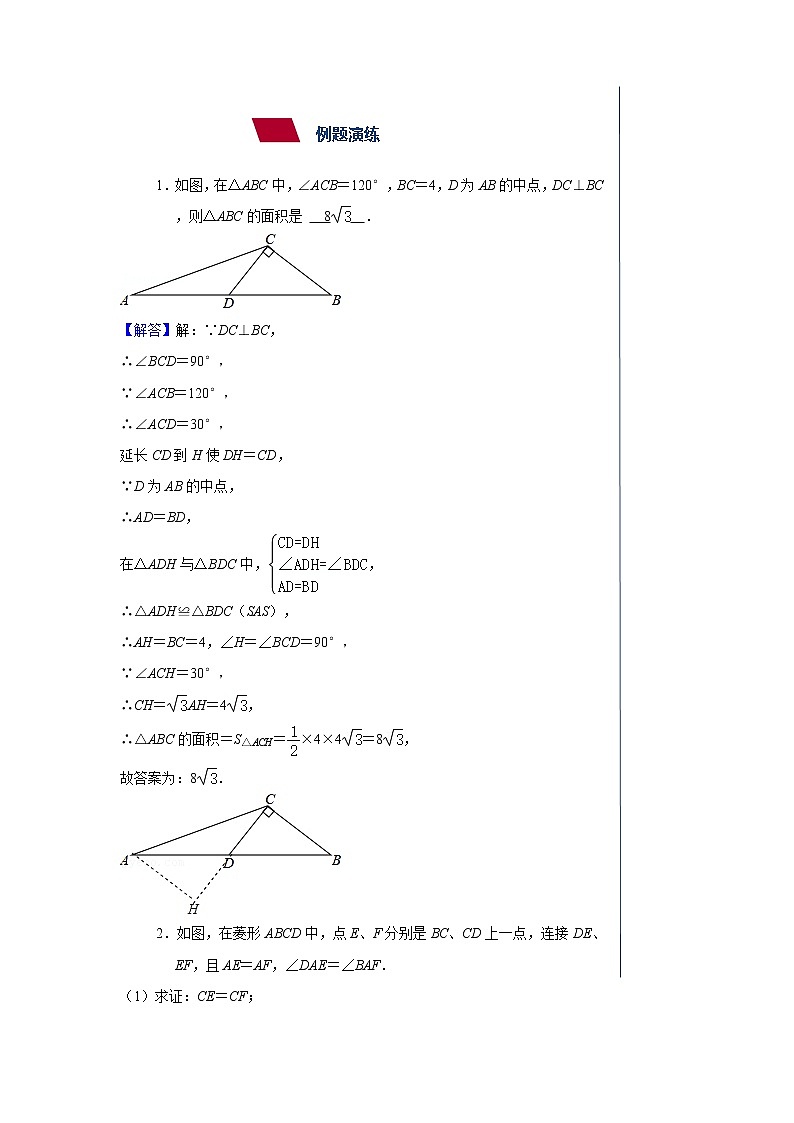
例题演练


1．如图，在△ABC中，∠ACB＝120°，BC＝4，D为AB的中点，DC⊥BC，则△ABC的面积是 　8　．

【解答】解：∵DC⊥BC，
∴∠BCD＝90°，
∵∠ACB＝120°，
∴∠ACD＝30°，
延长CD到H使DH＝CD，
∵D为AB的中点，
∴AD＝BD，
在△ADH与△BDC中，，
∴△ADH≌△BDC（SAS），
∴AH＝BC＝4，∠H＝∠BCD＝90°，
∵∠ACH＝30°，
∴CH＝AH＝4，
∴△ABC的面积＝S△ACH＝×4×4＝8，
故答案为：8．

2．如图，在菱形ABCD中，点E、F分别是BC、CD上一点，连接DE、EF，且AE＝AF，∠DAE＝∠BAF．
（1）求证：CE＝CF；
（2）若∠ABC＝120°，点G是线段AF的中点，连接DG，EG．求证：DG⊥GE．

【解答】证明：（1）∵四边形ABCD是菱形，
∴AB＝AD＝DC＝BC．
∵∠DAE＝∠BAF，
∴∠BAE＝∠DAF．
在△ABE与△ADF中，
，
∴△ABE≌△ADF（SAS），
∴BE＝DF，
∴BC﹣BE＝DC﹣DF，即CE＝CF；

（2）如图，延长EG到点H，使HG＝EG，连接HA、HD．
∵点G是AF的中点，
∴AG＝FG，
在△HAG与△EFG中，
，
∴△HAG≌△EFG（SAS），
∴EF＝AH，∠HAG＝∠EFG，
∴AH∥EF．
∵四边形ABCD是菱形，
∴DC＝BC＝AD．
∵由（1）知，BE＝DF，且∠BAE＝∠DAF，EC＝FC．
∵∠ABC＝120°，
∴∠C＝60°，
∴△EFC是等边三角形，
∴∠FEC＝60°，
∴EC＝FE．
由上述知，FE＝HA，
∴EC＝HA，∠HAG＝∠HAD+∠DAF＝∠EFG．
∵AF＝AE，
∴∠AFE＝∠AEF．
∵∠BAD＝60°，
∴∠EAF＝60°﹣∠BAE﹣∠DAF＝60°﹣2∠DAF．
在△AEF中，∠EAF＝180°﹣∠AEF﹣∠EFG＝180°﹣2∠EFG＝180°﹣2（∠HAD+∠DAF），
∴∠HAD＝60°．
在△HAD与△ECD中，
，
∴△HAD≌△ECD（SAS），
∴DE＝DH，
易证△DGH≌△DGE，
故∠DGH＝∠DGE＝90°，即DG⊥GE．




强化训练


1．如图在△ABC中，AD为BC边上的中线，E是线段AD上一点，且AE＝BC，BE的延长线交AC于F，若AF＝EF．
求证：（1）AC＝BE
（2）∠ADC＝60°．

【解答】证明：（1）倍长AD至点T，连BT．
在△ACD和△TBD中，

∴△ACD≌△TBD，
∴AC＝BT，∠CAD＝∠T，
又∵AF＝EF，
∴∠CAD＝∠AEF＝∠BET，
∴BT＝BE，
∴BE＝AC．

（2）在DT上取DM＝DC，连接BM．
∴AE+ED＝ED+DM
即AD＝EM
∴△DAC≌△MEB （SAS），
∴BM＝CD＝BD，
∴△BDM为正三角形，
∴∠ADC＝∠BDM＝60°．

2．【证明体验】
（1）如图1，在△ABC中，AD为BC边上的中线，延长AD至E，使DE＝AD，连结BE．求证：△ACD≌△EBD．
【迁移应用】
（2）如图2，在△ABC中，AC＝5，BC＝13，D为AB的中点，DC⊥AC．求△ABC面积．
【拓展延伸】
（3）如图3，在△ABC中，∠ABC＝90°，D是BC延长线上一点，BC＝CD，F是AB上一点，连结FD交AC于点E，若AF＝EF＝2，BD＝6，求ED的长．


【解答】（1）证明：如图1中，

在△ACD和△EBD中，
，
∴△ACD≌△EBD（SAS）；

（2）解：如图2中，延长CD到T，使得DT＝CD，连接BT．

由（1）可知△ADC≌△BDT，
∴AC＝BT＝5，∠ACD＝∠T＝90°，
∴CT＝＝＝12，
∴CD＝DT＝6，
∴S△ACB＝S△ADC+S△CDB＝•AC•DC+•BT•CD＝×5×6+×5×6＝30；

（3）解：如图3中，延长AC到R，使得CR＝CA，连接DR．

由（1）可知，△ACB≌△RCD，
∴AB＝DR，∠A＝∠R，
∵FE＝FA，
∴∠A＝∠AEF，
∵∠AEF＝∠DER，
∴∠DER＝∠R，
∴DE＝DR＝AB，
设DE＝DR＝AB＝x，则BF＝x﹣2，DF＝x+2，
在Rt△DBF中，BF2+BD2＝DF2，
∴（x﹣2）2+62＝（x+2）2，
∴x＝，
∴DE＝．
3．如图，在△ABC中，AD交BC于点D，点E是BC的中点，EF∥AD交CA的延长线于点F，交EF于点G．若BG＝CF，求证：AD为△ABC的角平分线．

【解答】解：延长FE，截取EH＝EG，连接CH，

∵E是BC中点，
∴BE＝CE，
在△BEG和△CEH中，
，
∴△BEG≌△CEH（SAS），
∴∠BGE＝∠H，BG＝CH，
∴∠BGE＝∠FGA＝∠H，
∵CF＝BG，
∴CH＝CF，
∴∠F＝∠H＝∠FGA，
∵EF∥AD，
∴∠F＝∠CAD，∠BAD＝∠FGA，
∴∠CAD＝∠BAD，
∴AD平分∠BAC．
4．已知：如图所示，AB＝BC，AD为△ABC中BC边的中线，延长BC至E点，使CE＝BC，连接AE．求证：∠DAC＝∠CAE．

【解答】解：延长AD到F，使得DF＝AD，连接CF．

∵AD＝DF，∠ADB＝∠FDC，BD＝DC，
∴△ADB≌△FDC（SAS），
∴AB＝CF，∠B＝∠DCF，
∵BA＝BC，CE＝CB
∴∠BAC＝∠BCA，CE＝CF，
∵∠ACE＝∠B+∠BAC，∠ACF＝∠DCF+∠ACB，
∴∠ACF＝∠ACE，∵AC＝AC，
∴△ACF≌△ACE（SAS），
∴∠CAD＝∠CAE．
5．在菱形ABCD和正三角形BGF中，∠ABC＝60°，P是DF的中点，连接PG、PC．

（1）如图1，当点G在BC边上时，若AB＝10，BF＝4，求PG的长；
（2）如图2，当点F在AB的延长线上时，线段PC、PG有怎样的数量关系，写出你的猜想；并给予证明．
（3）如图3，当点F在CB的延长线上时，（2）问中关系还成立吗？写出你的猜想，并给予证明．
【解答】（1）解：如图1：

延长GP交DC于点E，
利用△PED≌△PGF，得出PE＝PG，DE＝FG，
∵△BGF是等边三角形，
∴FG＝BG，
又∵四边形ABCD是菱形，
∴CD＝CB，
∴CE＝CG，
∴CP是EG的中垂线，在Rt△CPG中，∠PCG＝60°，
∵AB＝10，BF＝4；
∴CG＝6
∴PG＝3
（2）如图2，

证明：延长GP交DA于点E，连接EC，GC，
∵∠ABC＝60°，△BGF正三角形
∴GF∥BC∥AD，
∴∠EDP＝∠GFP，
在△DPE和△FPG中

∴△DPE≌△FPG（ASA）
∴PE＝PG，DE＝FG＝BG，
∵∠CDE＝∠CBG＝60°，CD＝CB，
在△CDE和△CBG中，

∴△CDE≌△CBG（SAS）
∴CE＝CG，∠DCE＝∠BCG，
∴∠ECG＝∠DCB＝120°，
∵PE＝PG，
∴CP⊥PG，∠PCG＝∠ECG＝60°
∴PG＝PC．
（3）猜想：PG＝PC．
证明：如图3，

延长GP到H，使PH＝PG，连接CH，CG，DH，作FE∥DC
∵P是线段DF的中点，
∴FP＝DP，
∵∠GPF＝∠HPD，
∴△GFP≌△HDP，
∴GF＝HD，∠GFP＝∠HDP，
∵∠GFP+∠PFE＝120°，∠PFE＝∠PDC，
∴∠CDH＝∠HDP+∠PDC＝120°，
∵四边形ABCD是菱形，
∴CD＝CB，∠ADC＝∠ABC＝60°，点A、B、G又在一条直线上，
∴∠GBC＝120°，
∵△BFG是等边三角形，
∴GF＝GB，
∴HD＝GB，
∴△HDC≌△GBC，
∴CH＝CG，∠DCH＝∠BCG，
∴∠DCH+∠HCB＝∠BCG+∠HCB＝120°，即∠HCG＝120°
∵CH＝CG，PH＝PG，
∴PG⊥PC，∠GCP＝∠HCP＝60°，
∴PG＝PC．
6．已知：在Rt△ABC中，AB＝BC，在Rt△ADE中，AD＝DE，连接EC，取EC的中点M，连接DM和BM．
（1）若点D在边AC上，点E在边AB上且与点B不重合，如图1，探索BM、DM的关系并给予证明；
（2）如果将图1中的△ADE绕点A逆时针旋转小于45°的角，如图2，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明．

【解答】解：（1）BM＝DM，BM⊥DM，
在Rt△EBC中，M是斜边EC的中点，
∴BM＝EC＝EM＝MC，
∴∠EMB＝2∠ECB．
在Rt△EDC中，M是斜边EC的中点，
∴DM＝EC＝EM＝MC．
∴∠EMD＝2∠ECD．
∴BM＝DM，∠EMD+∠EMB＝2（∠ECD+∠ECB），
∵∠ECD+∠ECB＝∠ACB＝45°，
∴∠BMD＝2∠ACB＝90°，即BM⊥DM．

（2）：（1）中的结论仍成立，
延长DM至点F，使得DM＝MF，连接CD和EF，连接BD，连接BF、FC，延长ED交AC于点H．
∵DM＝MF，EM＝MC，
∴四边形CDEF是平行四边形，
∴DE∥CF，ED＝CF，
∵ED＝AD，
∴AD＝CF．
∵DE∥CF，
∴∠AHE＝∠ACF．
∵∠BAD＝45°﹣∠DAH＝45°﹣（90°﹣∠AHE）＝∠AHE﹣45°，∠BCF＝∠ACF﹣45°，
∴∠BAD＝∠BCF．
又∵AB＝BC，
∴△ABD≌△CBF，
∴BD＝BF，∠ABD＝∠CBF，
∵∠ABD+∠DBC＝∠CBF+∠DBC，
∴∠DBF＝∠ABC＝90°．
在Rt△DBF中，由BD＝BF，DM＝MF，得BM＝DM且BM⊥DM．

7．如图1，在△ABC中，∠BAC＝90°，AB＝AC．
（1）若点M为AC上的任意一点，过M作MN⊥BC于点N，连接BM，取BM的中点D，连接AD、DM，求证：AD＝DN．
（2）如图2，若M为BC上的任意一点，以线段CM为底边作等腰Rt△MCN，此时，取BM的中点D，连接AD、DN，则AD与DN有怎样的数量关系？说明理由．
（3）如图3，在（2）的条件下将Rt△MNC绕C点旋转任意角度，连接BM，取BM的中点D，再连接AD、DN，则（2）中的结论仍然成立吗，它们之间又有怎样的位置关系？请说明理由．

【解答】（1）证明：解法一：如图1中，延长AD到K，使得DK＝AD，连接AN、KN、KM．

在△ADB和△KDM中，
，
∴△ADB≌△KDM，
∴AB＝KM＝AC，∠BAD＝∠MKD，
∴AB∥KM，
∴∠KMC＝∠BAC＝90°，
∵AB＝AC，∠BAC＝90°，
∴∠C＝45°，∵MN⊥BC，
∴∠MNC＝90°，∠NMC＝45°＝∠KMC＝∠C，
∴MN＝NC，
在△ANC和△KNM中，
，
∴△ANC≌△KNM，
∴AN＝KN，∠ANC＝∠KNM，
∴∠KNA＝∠MNC＝90°
∵AD＝DK，
∴DN＝AD＝DK，
即AD＝DN．
解法二：根据直角三角形斜边中线性质，可知AD＝BM，DN＝BM，由此即可证明．

（2）如图2中，结论：AD＝DN．
理由：延长AD到K，使得DK＝AD，连接AN、KN、KM．

在△ADB和△KDM中，
，
∴△ADB≌△KDM，
∴AB＝KM＝AC，∠BAD＝∠MKD，
∴AB∥KM，
∴∠KMD＝∠B＝45°，
∵∠NMC＝∠NCM＝∠ACB＝45°
∴MN＝NC，∠KMN＝∠ACN＝90°
在△ANC和△KNM中，
，
∴△ANC≌△KNM，
∴AN＝KN，∠ANC＝∠KNM，
∴∠KNA＝∠MNC＝90°
∵AD＝DK，
∴DN＝AD＝DK，
即AD＝DN．

（3）如图3中，结论：AD＝DN，AD⊥DN．
理由：延长AD到K，使得DK＝AD，连接AN、KN、KM，延长KN交AC于G．

在△ADB和△KDM中，
，
∴△ADB≌△KDM，
∴AB＝KM＝AC，∠BAD＝∠MKD，
∴AB∥KM，
∴∠KGC＝∠BAC＝90°，
∴∠ACN+∠NMG＝180°，
∵∠KMN+∠NMG＝180°，
∴∠ACN＝∠NMK，
在△ANC和△KNM中，
，
∴△ANC≌△KNM，
∴AN＝KN，∠ANC＝∠KNM，
∴∠KNA＝∠MNC＝90°
∵AD＝DK，
∴DN＝AD＝DK，DN⊥AK，
即AD＝DN．AD⊥DN．
8．△ABC中，点D为BC上一点，E为AC上一点，连接AD，BE，DE，已知BD＝DE，AD＝DC，∠ADB＝∠EDC．
（1）如图1，若∠ACB＝40°，求∠BAC的度数；
（2）如图2，F是BE的中点，过点F作AD的垂线，分别交AD、AC于点G、H．求证：AH＝CH．

【解答】解：（1）如图1，∵AD＝DC，∠ACB＝40°，
∴∠DAC＝∠ACB＝40°，
∴∠ADB＝∠C+∠DAC＝80°，
在△ADB和△CDE中，
∵，
∴△ADB≌△CDE（SAS），
∴∠BAD＝∠ACB＝40°，
∴∠BAC＝40°+40°＝80°；

（2）如图2，过B作BN∥AC，交HF的延长线于N，直线HF交AB于M，连接DH、DM，
∴∠BNM＝∠EHF，
∵BF＝EF，∠BFN＝∠EFH，
∴△EFH≌△BFN（AAS），
∴BN＝EH，
由（1）得：∠BAD＝∠DAC，
∵FH⊥AD，
∴∠AGF＝∠AGH＝90°，
∵AG＝AG，
∴△AMG≌△AHG（ASA），
∴AH＝AM，∠AHM＝∠AMH，
∵∠AMH＝∠BMN，
∴∠BNM＝∠BMN，
∴BN＝BM，
∵△ABD≌△CED，
∴∠ABD＝∠CED，
∵BD＝DE，
∴△DEH≌△DBM，
∴∠BMD＝∠AHD，
∵AM＝AH，
∠BAD＝∠DAH，AD＝AD，
∴△AMD≌△AHD，
∴∠AMD＝∠AHD，
∴∠AMD＝∠BMD，
∵∠AMD+∠BMD＝180°，
∴∠AMD＝90°，
∴∠AHD＝90°，
∵AD＝CD，
∴AH＝CH．

9．直角三角形有一个非常重要的性质：直角三角形斜边上的中线等于斜边的一半，比如：如图1，Rt△ABC中，∠C＝90°，D为斜边AB中点，则CD＝AD＝BD＝AB．请你利用该定理和以前学过的知识解决下列问题：
如图2，在△ABC中，点P为BC边中点，直线a绕顶点A旋转，若B、P在直线a的异侧，BM⊥直线a于点M，CN⊥直线a于点N，连接PM、PN；
（1）求证：PM＝PN；
（2）若直线a绕点A旋转到图3的位置时，点B、P在直线a的同侧，其它条件不变，此时PM＝PN还成立吗？若成立，请给予证明：若不成立，请说明理由；
（3）如图4，∠BAC＝90°，a旋转到与BC垂直的位置，E为BC上一点且AE＝AC，EN⊥a于N，连接EC，取EC中点P，连接PM，PN，求证：PM⊥PN．

【解答】（1）证明：如图2中，延长NP交BM的延长线于G．

∵BM⊥AM，CN⊥AM，
∴BG∥CN，
∴∠PCN＝∠PBG，
在△PNC和△PGB中，
，
∴△PNC≌△PGB，
∴PN＝PG，
∵∠NMG＝90°，
∴PM＝PN＝PG．

（2）解：结论：PM＝PN．
如图3中，延长NP交BM于G．

∵BM⊥AM，CN⊥AM，
∴BM∥CN，
∴∠PCN＝∠PBG，
在△PNC和△PGB中，
，
∴△PNC≌△PGB，
∴PN＝PG，
∵∠NMG＝90°，
∴PM＝PN＝PG．

（3）如图4中，延长NP交BM于G．

∵∠EAN+∠CAM＝90°，∠CAM+∠ACM＝90°，
∴∠EAN＝∠ACM，
在△EAN和△CAM中，
，
∴△EAN≌△CAM，
∴EN＝AM，AN＝CM，
∵EN∥CG，
∴∠ENP＝∠CGP，
在△ENP和△CGP中，
，
∴△ENP≌△CGP，
∴EN＝CG＝AM，PN＝PG，
∵AN＝CM，
∴MG＝MN，
∴PM⊥PN．



1．（2017•唐河县四模真题）已知△ABC和△ADE是等腰直角三角形，∠ACB＝∠ADE＝90°，点F为BE中点，连接DF、CF．
（1）如图1，当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；
（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；
（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD＝1，AC＝，求此时线段CF的长（直接写出结果）．

【解答】解：（1）∵∠ACB＝∠ADE＝90°，点F为BE中点，
∴DF＝BE，CF＝BE，
∴DF＝CF．
∵△ABC和△ADE是等腰直角三角形，
∴∠ABC＝45°
∵BF＝DF，
∴∠DBF＝∠BDF，
∵∠DFE＝∠ABE+∠BDF，
∴∠DFE＝2∠DBF，
同理得：∠CFE＝2∠CBF，
∴∠EFD+∠EFC＝2∠DBF+2∠CBF＝2∠ABC＝90°，
∴DF＝CF，且DF⊥CF．
（2）（1）中的结论仍然成立．
证明：如图，此时点D落在AC上，延长DF交BC于点G．
∵∠ADE＝∠ACB＝90°，
∴DE∥BC．
∴∠DEF＝∠GBF，∠EDF＝∠BGF．
∵F为BE中点，
∴EF＝BF．
∴△DEF≌△GBF．
∴DE＝GB，DF＝GF．
∵AD＝DE，
∴AD＝GB，
∵AC＝BC，
∴AC﹣AD＝BC﹣GB，
∴DC＝GC．
∵∠ACB＝90°，
∴△DCG是等腰直角三角形，
∵DF＝GF．
∴DF＝CF，DF⊥CF．
（3）延长DF交BA于点H，
∵△ABC和△ADE是等腰直角三角形，
∴AC＝BC，AD＝DE．
∴∠AED＝∠ABC＝45°，
∵由旋转可以得出，∠CAE＝∠BAD＝90°，
∵AE∥BC，
∴∠AEB＝∠CBE，
∴∠DEF＝∠HBF．
∵F是BE的中点，
∴EF＝BF，
∴△DEF≌△HBF，
∴ED＝HB，
∵AC＝，在Rt△ABC中，由勾股定理，得
AB＝4，
∵AD＝1，
∴ED＝BH＝1，
∴AH＝3，在Rt△HAD中由勾股定理，得
DH＝，
∴DF＝，
∴CF＝
∴线段CF的长为．