2022-2023学年四川省什邡市七年级下册数学期末专项突破模拟（AB卷）含解析

这是一份2022-2023学年四川省什邡市七年级下册数学期末专项突破模拟（AB卷）含解析，共41页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。

2022-2023学年四川省什邡市七年级下册数学期末专项突破模拟
（A卷）
一、选一选（共10小题，每题4分，满分40分）
1. 下列图案中既是对称图形，又是轴对称图形的是（ ）
A B. C. D.
2. 若x＞y，则下列式子错误的是（ ）
A. x﹣3＞y﹣3 B. ﹣3x＞﹣3y C. x+3＞y+3 D.
3. 如图，已知△ABC≌△ADE，∠D=59°，∠AED=78°，则∠C的大小是（ ）

A. 43° B. 53° C. 59° D. 78°
4. 现有四根木棒，长度分别为4，6，8，10，从中任取三根木棒，能组成三角形的个数为（ ）
A. 1个 B. 2个 C. 3个 D. 4个
5. 已知方程组，与y的值之和等于2，则的值等于（ ）
A. 3 B. C. 4 D.
6. 如图所示，某同学把一块三角形的玻璃没有小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪一块去（　　）

A. ① B. ② C. ③ D. ①和②
7. 若满足下列某个条件，则它没有是直角三角形的是( )
A. B. C. D.
8 能铺满地面的正多边形的组合是（　　）
A. 正五边形和正方形 B. 正六边形和正方形
C. 正八边形和正方形 D. 正十边形和正方形
9. 已知x=2是没有等式的解，且x=1没有是这个没有等式的解，则实数a的取值范围是（　　）
A. a＞1 B. a≤2 C. 1＜a≤2 D. 1≤a≤2
10. 如图线段AB与直线AC相交构成∠BAC(其中∠BAC为锐角，且∠BAC≠60°) ,请在直线AC上找一点D使得△ABD为等腰三角形．问：这样的点D共存在( )个．

A. 1 B. 2 C. 3 D. 4
二、填 空 题（共6小题，每题4分，满分24分）
11. 没有等式组解集是_______
12. 如图，自行车车身为三角形结构，这样做根据的数学道理是____________.

13. 如图，将△ACB绕点C顺时针方向旋转43°得△A’CB’，若AC⊥A’B’，则∠BAC＝___度．

14. 如图，已知，那么添加下列一个条件____________________，使得．

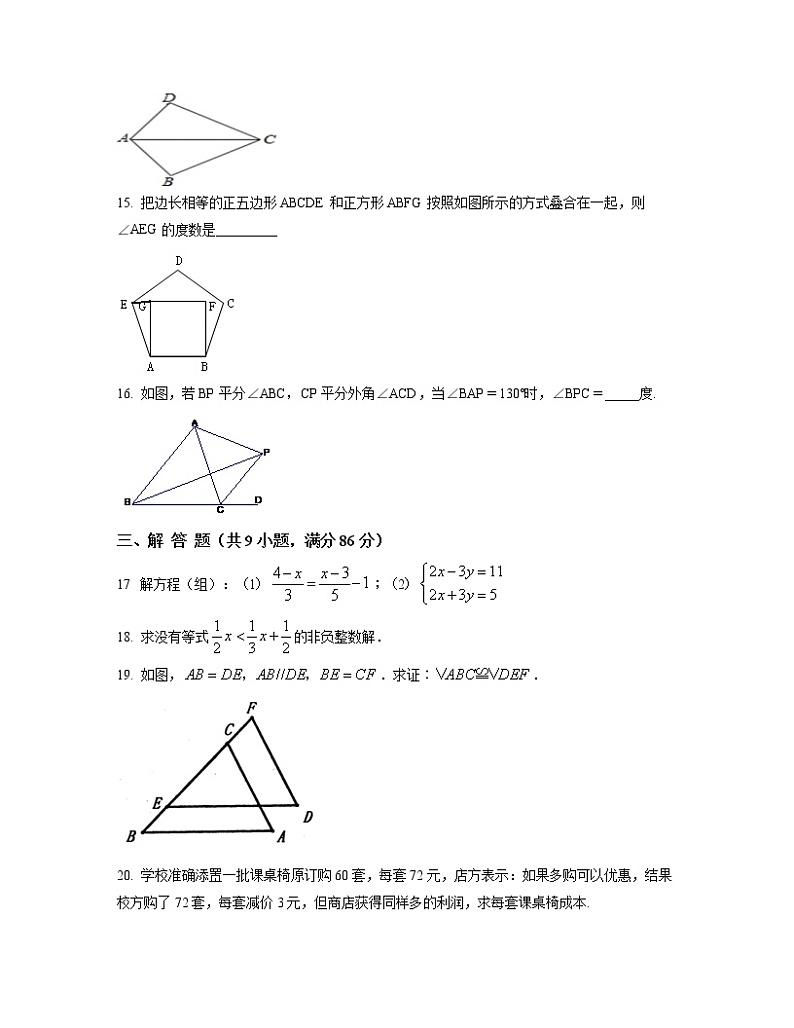
15. 把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起，则∠AEG的度数是_________

16. 如图，若BP平分∠ABC，CP平分外角∠ACD，当∠BAP＝130°时，∠BPC＝_____度.

三、解 答 题（共9小题，满分86分）
17 解方程（组）：（1）；（2）
18. 求没有等式的非负整数解．
19. 如图，．求证∶．

20. 学校准确添置一批课桌椅原订购60套，每套72元，店方表示：如果多购可以优惠，结果校方购了72套，每套减价3元，但商店获得同样多的利润，求每套课桌椅成本.
21. 如图,在△ABC中,DE是AC的垂直平分线.
（1）若AE=6,则AC＝　　　；
（2）若∠ABD=40º，∠ADB=70º，求∠BAC的度数.

22. 我们知道：对称的直线可以把一个对称图形的面积平分．
请运用这一性质解决下列问题：（注意：以下作图工具仅限于一把无刻度的直尺，要体现作图过程且保留作图痕迹）

（1）如甲图，画一条直线把矩形分成面积相等的两部分；
（2）如乙图，画一条直线把乙图分成面积相等的两部分(画出3种没有同的分割线)．

23. 如图，边长为8的等边和等边互相重合，现将沿直线向左平移个单位，将沿直线向右平移个单位.
（1）若＝2，则BE=　　　；
（2）当、是线段的三等分点时，则的值为多少.

24. 在边长为1的小正方形组成的方格纸中，若多边形的每个顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形.记格点多边形内的格点数为，边界上的格点数为，则格点多边形的面积可表示为，其中，为常数.
（1）在下面的两张方格纸中各有一个格点多边形，依次为、正方形.认真数一数：内的格点数是_______，正方形边界上的格点数是_______;

（2）利用（1）中的两个格点多边形确定，的值;
（3）现有一张方格纸共有110个格点，画有一个格点多边形，它的面积，若该格点多边形外的格点数为.
①填空：若，则＝　　　　　；
②若，求的值．(写出解答过程)
25. （1）如图1，在△ABC中∠A＝60 º，BD、CE均为△ABC的角平分线且相交于点O.
①填空：∠BOC＝ 度；
②求证：BC＝BE+CD．(写出求证过程)
（2）如图2，在△ABC中，AB=AC=m，BC=n， CE平分∠ACB．
①若△ABC的面积为S，在线段CE上找一点M，在线段AC上找一点N，使得AM+MN的值最小，则AM+MN的最小值是　　 　　　　．(直接写出答案)；　
②若∠A=20°，则△BCE的周长等于　　　　　　．(直接写出答案)．





2022-2023学年四川省什邡市七年级下册数学期末专项突破模拟
（A卷）
一、选一选（共10小题，每题4分，满分40分）
1. 下列图案中既是对称图形，又是轴对称图形的是（ ）
A. B. C. D.
【正确答案】D

【分析】根据对称图形以及轴对称图形的定义逐项判断即可．在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做对称图形；如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形．
【详解】解：A．没有是对称图形，是轴对称图形，此选项错误；
B．是对称图形，没有是轴对称图形，此选项错误；
C．没有是对称图形，是轴对称图形，此选项错误；
D．既是对称图形，又是轴对称图形，此选项正确；
故选：D．
本题考查的知识点是识别对称图形以及轴对称图形，掌握对称图形以及轴对称图形的特征是解此题的关键．
2. 若x＞y，则下列式子错误的是（ ）
A. x﹣3＞y﹣3 B. ﹣3x＞﹣3y C. x+3＞y+3 D.
【正确答案】B

【分析】根据没有等式的性质在没有等式两边加（或减）同一个数（或式子），没有等号的方向没有变；没有等式两边乘（或除以）同一个正数，没有等号的方向没有变；没有等式两边乘（或除以）同一个负数，没有等号的方向改变即可得出答案．
【详解】解：A、没有等式两边都减3，没有等号的方向没有变，正确，故本选项没有符合题意；
B、乘以一个负数，没有等号方向改变，错误，故本选项符合题意；
C、没有等式两边都加3，没有等号的方向没有变，正确，故本选项没有符合题意；
D、没有等式两边都除以一个正数，没有等号的方向没有变，正确故本选项没有符合题意．
故选：B．
3. 如图，已知△ABC≌△ADE，∠D=59°，∠AED=78°，则∠C的大小是（ ）

A. 43° B. 53° C. 59° D. 78°
【正确答案】D

【详解】∵△ABC≌△ADE，
∴∠C=∠AED=78°；
故选D.
4. 现有四根木棒，长度分别为4，6，8，10，从中任取三根木棒，能组成三角形的个数为（ ）
A. 1个 B. 2个 C. 3个 D. 4个
【正确答案】C

【分析】取四根木棒中的任意三根，共有4中取法，然后依据三角形三边关系定理将没有合题意的舍去．
【详解】解：共有4种：
①取4，6，8；由于8-4＜6＜8+4，能构成三角形；
②取4，8，10；由于10-4＜8＜10+4，能构成三角形；
③取4，6，10；由于6=10-4，没有能构成三角形，此种情况没有成立；
④取6，8，10；由于10-6＜8＜10+6，能构成三角形．
所以有3种符合要求．
故选：C．
此题考查构成三角形的条件，掌握三角形三边关系是解题的关键.
5. 已知方程组，与y的值之和等于2，则的值等于（ ）
A. 3 B. C. 4 D.
【正确答案】C

【分析】把方程组中的k看作常数，利用加减消元法，用含k的式子分别表示出x与y，然后根据x与y的值之和为2，列出关于k的方程，求出方程的解即可得到k的值．
【详解】，
①×2-②×3得：y=2（k+2）-3k=-k+4，
把y=-k+4代入②得：x=2k-6，
又x与y的值之和等于2，所以x+y=-k+4+2k-6=2，
解得：k=4
故选：C．
此题考查学生灵活利用消元法解方程组的能力，是一道基础题．此题的关键在于把k看作常数解方程组．
6. 如图所示，某同学把一块三角形的玻璃没有小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪一块去（　　）

A. ① B. ② C. ③ D. ①和②
【正确答案】C

【分析】观察每块玻璃形状特征，利用ASA判定三角形全等可得出答案．
【详解】解：块和第二块只保留了原三角形的一个角和部分边，根据这两块中的任一块均没有能配一块与原来完全一样的；第三块没有仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃．应带③去．
故选：C．
本题属于利用ASA判定三角形全等的实际应用，难度没有大，但形式较颖，要善于将所学知识与实际问题相，解题的关键是熟练掌握全等三角形的判定定理．
7. 若满足下列某个条件，则它没有是直角三角形的是( )
A. B. C. D.
【正确答案】D

【详解】A.∵∠A+∠B+∠C=180°，∠C=∠A+∠B，
∴∠C=90°，即三角形是直角三角形，故本选项错误；
B.∵∠A+∠B+∠C=180°，∠C=∠A−∠B，
∴∠A=90°，即三角形是直角三角形，故本选项错误；
C.∵∠A+∠B+∠C=180°，∠A:∠B:∠C=1:4:3
∴∠B=90°，即三角形是直角三角形，故本选项错误；
D.∵∠A+∠B+∠C=180°，∠A=2∠B=3∠C，
∴∠A≈98°，即三角形没有是直角三角形，故本选项正确；
故选D.
8. 能铺满地面的正多边形的组合是（　　）
A. 正五边形和正方形 B. 正六边形和正方形
C. 正八边形和正方形 D. 正十边形和正方形
【正确答案】C

【分析】分别求出各个多边形每个内角的度数，然后根据围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角判断即可.
【详解】正五边形每个内角是，正方形的每个内角是，，，显然取任何正整数时，没有能得正整数，故没有能铺满；
正方形的每个内角是，正六边形的每个内角是，，，显然取任何正整数时，没有能得正整数，故没有能铺满；
正方形的每个内角是，正八边形的每个内角为：，，正八边形和正方形能铺满.
故选.
几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
9. 已知x=2是没有等式的解，且x=1没有是这个没有等式的解，则实数a的取值范围是（　　）
A. a＞1 B. a≤2 C. 1＜a≤2 D. 1≤a≤2
【正确答案】C

【详解】∵x=2是没有等式(x−5)(ax−3a+2)⩽0的解，∴(2−5)(2a−3a+2)⩽0，解得：a⩽2，
∵x=1没有是这个没有等式的解，∴(1−5)(a−3a+2)>0，解得：a>1，
∴1 故选C.

10. 如图线段AB与直线AC相交构成∠BAC(其中∠BAC为锐角，且∠BAC≠60°) ,请在直线AC上找一点D使得△ABD为等腰三角形．问：这样的点D共存在( )个．

A. 1 B. 2 C. 3 D. 4
【正确答案】D

【详解】如图，

①AB的垂直平分线交AC一点D1(DA=DB),；
②以A为圆心,AB为半径画圆,交AC于D2 (此时AB=AD)；
③以B为圆心,BA为半径画圆,交BC有二点D3，D4(此时BD=BA).
故符合条件的点有4个.
故选D.
点睛：此题考查了等腰三角形的判定和性质，在没有明确等腰三角形的顶点时，要分情况进行讨论.
二、填 空 题（共6小题，每题4分，满分24分）
11. 没有等式组的解集是_______
【正确答案】

【详解】没有等式可化为：，
即；
∴没有等式组的解集为−2⩽x<0.
故答案为
12. 如图，自行车的车身为三角形结构，这样做根据的数学道理是____________.

【正确答案】三角形具有稳定性

【详解】自行车的车身为三角结构，这是因为三角形具有稳定性.
故答案为三角形具有稳定性.
13. 如图，将△ACB绕点C顺时针方向旋转43°得△A’CB’，若AC⊥A’B’，则∠BAC＝___度．

【正确答案】47

【详解】∵△ACB绕点C顺时针方向旋转43°得△A′CB′,点B与B′对应，
∴∠BCB′=∠ACA′=43°∠A=∠A′，
而AC⊥A′B′，
∴∠CDA′=87°，
∴∠A′=90°−43°=47°，
∴∠A=∠A′=47°.
故答案为47.
14. 如图，已知，那么添加下列一个条件____________________，使得．

【正确答案】或或（添加一个即可）

【分析】添加的条件是：或或，根据三角形全等的判定定理或或即可推导出．
【详解】解：①添加的条件是：
理由是：在和中，

∴；
②添加的条件是：
理由是：在和中，

∴；
③添加的条件是：
理由是：在和中，

∴
故答案是：或或（添加一个即可）
本题考查了对全等三角形的判定的应用，是一个开放性题目，比较典型，难度也没有是很大．
15. 把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起，则∠AEG的度数是_________

【正确答案】81°

【详解】正五边形的内角的度数是×(5−2)×180°=108°，
正方形的内角是90°，
则∠EAG=108°−90°=18°，
∵AE=AG,
∴∠AEG=∠AGE=(180°-18°)=81°.
故答案为81°.
16. 如图，若BP平分∠ABC，CP平分外角∠ACD，当∠BAP＝130°时，∠BPC＝_____度.

【正确答案】40

【详解】如图：过P作PE⊥AB，PF⊥AC，PG⊥BC，

∵BP平分∠ABC，CP平分外角∠ACD，
∴PE=PF=PG，
∴∠PAC=∠PAE=50°,
∴∠BAC=80°,
∴∠BPC=∠PCD−∠PBC=∠ACD−∠ABC=∠BAC=40°.
故答案为40.
点睛：此题考查了三角形角平分线的定义和性质，三角形外角的性质，解题的关键是正确作出辅助线.
三、解 答 题（共9小题，满分86分）
17. 解方程（组）：（1）；（2）
【正确答案】(1) (2)

【详解】试题分析：（1）含有分母的一元方程，应先去分母，再去括号、移项、合并同类项、系数化成1，从而得到原方程的解；
（2）用“加减法”求解，通过两个方程相加消去y，即得出一个关于x的方程，求出x的值，将x的值代入原方程组的任一个方程，求出y的值，从而求出了原方程组的解．
试题解析：（1）去分母,得5(4-x) =3(x-3)−15，
去括号，得20-5x=3x-9-15，
移项，得−5x−3x=−9-15-20，
合并同类项，得−8x=-44，
方程两边同除以−8，得x=−.
所以，原方程的解为；
（2）
①+②，得4x=16，x=4，
把x=4带入②，得2×4+3y=5，
解得y=-1，
所以方程组的解为.
18. 求没有等式的非负整数解．
【正确答案】非负整数解为＝0，1，2.

【详解】试题分析：根据解一元没有等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得没有等式的解集，根据解集可得其非负整数解．
试题解析：去分母，得：3x<2x+3，
移项，得： 3x−2x<3，
合并同类项，得： x<3，
∴没有等式的非负整数解为0、1、2.
19. 如图，．求证∶．

【正确答案】证明见解析

【分析】根据即可证明．
【详解】证明∶



即
在和中


此题主要考查全等三角形的判定，解题的关键是熟知全等三角形的判定定理．
20. 学校准确添置一批课桌椅原订购60套，每套72元，店方表示：如果多购可以优惠，结果校方购了72套，每套减价3元，但商店获得同样多的利润，求每套课桌椅成本.
【正确答案】每套课桌椅成本54元.

【详解】试题分析：每套利润×套数=总利润，在本题中有两种，虽然单价没有同，但是总利润相等，可依此列方程解应用题．
试题解析：设每套课桌椅成本元，
由题意得：，
解得，
经检验，符合题意，
答：每套课桌椅成本54元.
21. 如图,在△ABC中,DE是AC的垂直平分线.
（1）若AE=6,则AC＝　　　；
（2）若∠ABD=40º，∠ADB=70º，求∠BAC的度数.

【正确答案】（1）12；（2）∠BAC＝105°

【详解】试题分析：（1）由线段垂直平分线的性质可得：AE=CE，即可求得AC值；
（2）由线段垂直平分线的性质得DA＝DC，由等边对等角，得∠DAC＝∠C，由外角的性质，可求得∠C＝35°，再由三角形外角和定理可得∠BAC度数.
试题解析：（1）∵DE是AC的垂直平分线，
∴AE=CE=6，
∴AC=2AE=12；
故答案为12；
(2) ∵DE是AC的垂直平分线,
∴DA＝DC，
∴∠DAC＝∠C，
又∵∠ADB为△ADC的外角，
∴∠DAC＋∠C＝∠ADB=70º，
∴∠DAC＝∠C＝35°，
在△ABC中，∠BAC＋∠ABD＋∠C＝180°.
∴∠BAC＝180°－∠ABD－∠C＝180°－40º－35°＝105°.
22. 我们知道：对称的直线可以把一个对称图形的面积平分．
请运用这一性质解决下列问题：（注意：以下作图工具仅限于一把无刻度的直尺，要体现作图过程且保留作图痕迹）

（1）如甲图，画一条直线把矩形分成面积相等的两部分；
（2）如乙图，画一条直线把乙图分成面积相等的两部分(画出3种没有同的分割线)．

【正确答案】画图见解析.

【详解】试题分析：（1）矩形是对称图形，因而所画直线对称就能满足要求；
（2）只要作两个长方形的直线即可．
试题解析：（1）如图：

（2）画图如下：

23. 如图，边长为8的等边和等边互相重合，现将沿直线向左平移个单位，将沿直线向右平移个单位.
（1）若＝2，则BE=　　　；
（2）当、是线段的三等分点时，则的值为多少.

【正确答案】（1）4；（2）的值为2或8．

【详解】试题分析：（1）根据点平移的性质可得出BE=2m，代入m的值即可得出结论；
（2）分点E、C的位置没有同，两种情况来考虑，根据线段间的关系BC=4即可得出关于m的一元方程，解方程即可得出结论．
试题解析：∵点B向左平移m个单位，点E向右平移m个单位，
∴BE=2m，
∵m=2，
∴BE=2m=4.
故答案为4；
(2)E、C是线段BF的三等分点分两种情况：
①点E在点C的左边时,如图1所示：

∵E、C是线段BF的三等分点，
∴BE=EC=CF，
∵BC=8，BE=2m，
∴2m=4，解得：m=2；
②点E在点C的右边时，如图2所示：

∵E、C是线段BF的三等分点，
∴BC=CE=EF，
∵BC=8，BE=2m，
∴2m=8×2，解得：m=8.
综上可知：当E. C是线段BF的三等分点时，m的值为2或8.
24. 在边长为1的小正方形组成的方格纸中，若多边形的每个顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形.记格点多边形内的格点数为，边界上的格点数为，则格点多边形的面积可表示为，其中，为常数.
（1）在下面的两张方格纸中各有一个格点多边形，依次为、正方形.认真数一数：内的格点数是_______，正方形边界上的格点数是_______;

（2）利用（1）中的两个格点多边形确定，的值;
（3）现有一张方格纸共有110个格点，画有一个格点多边形，它的面积，若该格点多边形外的格点数为.
①填空：若，则＝　　　　　；
②若，求的值．(写出解答过程)
【正确答案】（1）3，12；（2）；（3）①18；②＝7或8

【详解】试题分析：（1）利用格点图形的定义三角形以及正方形图形得出即可；
（2）利用已知图形，S=ma+-1得出关于m，n的关系式，进而求出即可；
（3）①由（2）知：，将S=40代入和a+b+c=110联立消去b即可求得a的值；②由，用a 表示出b，由用a表示出c，带入，即可解得a的范围，由于a为整数，再确定出a的值即可.
试题解析：（1）由图可得：内的格点数是3，正方形DEFG边界上的格点数是12；
（2）：面积×3×4=6，正方形DEFG面积为3×3=9，
依题意，得，解得；
（3）①∵a是多边形内的格点数，b是多边形边界上的格点数，c是多边形外的格点数，总格点数为110，
∴a+b+c=110，
∵,
∴a+2b =110,
由（2）知，
∴,解得a=18.
故答案为18；
②依题意，得解得
代入，得
解没有等式组，得
∴整数＝7或8.
点睛：本题考查新定义，考查学生分析解决问题的能力，注意区分多边形内部格点和边界个点数是关键.
25. （1）如图1，在△ABC中∠A＝60 º，BD、CE均为△ABC的角平分线且相交于点O.
①填空：∠BOC＝ 度；
②求证：BC＝BE+CD．(写出求证过程)
（2）如图2，在△ABC中，AB=AC=m，BC=n， CE平分∠ACB．
①若△ABC的面积为S，在线段CE上找一点M，在线段AC上找一点N，使得AM+MN的值最小，则AM+MN的最小值是　　 　　　　．(直接写出答案)；　
②若∠A=20°，则△BCE的周长等于　　　　　　．(直接写出答案)．

【正确答案】（1）①120；②证明见解析；（2）①(或)；②m

【详解】试题分析：（1）①根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB，则2∠BOC=360°-2∠OBC-2∠OCB，再根据角平分线定义得∠ABC=2∠OBC，∠ACB=2∠OCB，则2∠BOC=360°-∠ABC-∠ACB，易得∠BOC=90°+∠A，由∠A＝60 º即可得∠BOC的值；
②采用截长法在在BC上截取BF＝BE，连接OF，由边角边证得△EBO≌△FBO，再由角边角证得△DCO≌△FCO，即可得证；
（2）①当AM⊥BC时，AM+MN的值最小；
②在CA上截取CD=CB,以E为圆心EC为半径画弧，与AC交于点F，通过构造全等三角形，利用等腰三角形的判定和性质即可求解.
试题解析：（1）①在△OBC中，∠BOC=180°-∠OBC-∠OCB，
∴2∠BOC=360°-2∠OBC-2∠OCB，
∵BD、CE均为△ABC的角平分线，
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
∴2∠BOC=360°-∠ABC-∠ACB，
∴∠BOC=90°+∠A，
∵∠A＝60 º，
∴∠BOC=90°+×60 º=120°；
故答案为120°；
②证明：由（1）①∠BOC＝120°，
∴∠BOE＝∠COD＝180°－120°＝60°，
在BC上截取BF＝BE，连接OF，

∵BD平分∠ABC，
∴∠EBO＝∠FBO，
又∵BO＝BO(公共边相等)
∴△EBO≌△FBO(SAS)
∴∠BOF＝∠BOE＝60°，
∴∠COF＝∠BOC－∠BOF＝120°－60°＝60°＝∠COD，
∵CE平分∠ACB，
∴∠DCO＝∠FCO，
又∵CO＝CO(公共边相等)
∴△DCO≌△FCO(ASA)
∴CD＝CF，
∴BC＝BF+CF＝BE+CD；
（2）①如图：

当AM⊥BC时，与BC交于点D，过M作MN⊥AC交AC与点D，
∵CE平分∠ACB，
∴DM=DN，
∴AD=AM+MD=AM+MN,
此时，AM+MN的值最小，
由S△ABC=BC·AD，BC=n，△ABC的面积为S，
得AD=，
或∵AB=AC, AD⊥BC, AB=AC=m，BC=n，
∴BD=CD=,
在Rt△ACD中，由勾股定理得AD=；
故答案为(或)；
②如图：在CA上截取CD=CB,以E圆心EC为半径画弧，与AC交于点F，

∵AB=AC=m，∠A=20°，
∴∠B=∠C=80°,
∵CE平分∠ACB,
∴∠BCE=∠DCE=40°,
∵CE=CE,
∴△BCE≌△DCE,
∴∠CDE=∠B=80°,∠DEC=∠BEC=60°,BE=DE,
∴∠CDE=40°,
∵EC=EF,
∴∠EFC=∠ECF=40°,
∴∠DEF=∠CDE-∠DFE=40°,
∴DE=DF,
∠AEF=∠DFE-∠A=40°-20°=20°,
∴EF=AF,
∴BE=DF,CE=AF,
∴△BCE的周长=BC+CE+BE=CD+AF+DF=AC=m.
点睛：此题考查了角平分线的定义和性质，三角形内角和定理，等腰三角形的性质，最短路径问题等知识.解题的关键是添加正确的辅助线构造出全等三角形，对线段进行转化.


















2022-2023学年四川省什邡市七年级下册数学期末专项突破模拟
（B卷）
一、选一选（本大题共12小题，每小题3分，共36分）
1. -2的倒数是（ ）
A. -2 B. C. D. 2
2. 我国最长的河流长江全长约为6300千米，用科学记数法表示为（　　）
A. 63×102米 B. 6.3×103米 C. 6.3×106米 D. 6.3×105米
3. 单项式的系数与次数分别是（ ）
A. 3，4 B. -3，4 C. ，4 D. ，3
4. 下列计算正确的是（　　）
A. 3a+4=7ab B. 7x﹣3x=4
C. 3m+m=3m2 D. 3x2y﹣2x2y=x2y
5. 如果x=1是关于x的方程﹣x+a=3x﹣2的解，则a的值为（　　）
A. 1 B. ﹣1 C. 2 D. ﹣2
6. 将一副三角板按如图方式摆放在一起，且∠1比∠2大30°，则∠1的度数等于(　　)

A. B. C. D.
7. 过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图正确的为（　　）

A. B. C. D.
8. 某品牌电脑降价15%后，每台售价a元，则这种电脑的原价为每台（　　）元．
A. 0.85a B. 0.15a C. D.
9. 方程去分母正确的是（ ）.
A. x-1-x=-1 B. 4x-1-x=-4 C. 4x-1+x=-4 D. 4x-1+x=-1
10. 运用等式的性质变形，正确的是（ ）
A. 如果，那么 B. 如果，那么
C. 如果，那么 D. 如果那么
11. 若2x﹣1=3y﹣2，则6y﹣4x值是（　　）
A. 1 B. ﹣1 C. 2 D. ﹣2
12. 一组按规律排列的多项式： ，其中第10个式子是( )
A. B. C. D.
二、填 空 题（本大共1大题， 8小题，每小题3分共24分）
13. 若（m+3）2+|n﹣2|=0，则﹣mn=_____
14. 如果单项式3xa+2yb﹣2与5x3ya+2的和为8x3ya+2，那么a﹣b=_____．
15. 已知| x |= 8 ，| y |= 3，|x + y |=x+y ，则 x+y=___________
16. 若关于x的方程nxn﹣2﹣n+4=0为一元方程，则这个方程的解是____________．
17. 某校春游，若包租相同大巴13辆，那么就有14人没有座位；如果多包租1辆，那么就多了26个空位，若设春游的总人数为x人，则列方程为_____
18. 已知线段AB＝8cm，在直线AB上有一点C，且BC＝4cm，M是线段AC的中点，则线段AM的长为_____．
19. 如果一个角补角是150°，那么这个角的余角是_________°.
20. 如图，在1000个“〇”中依次填入一列数字m1，m2，m3…，m1000使得其中任意四个相邻“〇”中所填数字之和都等于﹣10，已知m25=x﹣1，m999=﹣2x，可得x的值为_____．

三、解 答 题
21. （1）计算 （﹣1）2×（﹣23）﹣（﹣4）÷2×
（2）先化简，再求值已知2（3a2b﹣5ab2）﹣3（2a2b﹣3ab2），其中a=﹣1，b=3．
（3）解方程：3（x﹣3）+1=x﹣（2x﹣1）
（4）解方程：﹣=2
22. 如图，已知∠COB=2∠AOC，OD平分∠AOB，∠COD=10°，求∠AOB的度数．

23. 如图，点在线段上，点分别是的中点．
（1）若，求线段MN 的长；
（2）若为线段上任一点，满足，其它条件没有变，你能求出的长度吗？请说明理由．
（3）若在线段的延长线上，且满足分别为 AC、BC的中点，你能求出的长度吗？请画出图形，写出你的结论，并说明理由．

24. （10分）下表是居民生活用气阶梯价格，
一般生活用气
　
户年天然气用量（m3）
价格
　
6口（含）以上
6口以下
档
0﹣500（含）
0﹣350（含）
228元/m3
第二档
500﹣650（含）
350﹣500（含）
2.5元/m3
第三档
650以上
500以上
3.9元/m3
（1）小明家6口人，2017年全年天然气用量为550m3，小明家需交多少费用？
（2）小华家5口人，2017年全年天然气共缴费1251元，请求出小华家2017年共用了多少m3天然气？
25. 如图，OC在∠BOD内．
（1）如果∠AOC和∠BOD都是直角．
①若∠BOC=60°，则∠AOD的度数是　 　；
②猜想∠BOC与∠AOD的数量关系，并说明理由；
（2）如果∠AOC=∠BOD=x°，∠AOD=y°，求∠BOC的度数．























2022-2023学年四川省什邡市七年级下册数学期末专项突破模拟
（B卷）
一、选一选（本大题共12小题，每小题3分，共36分）
1. -2的倒数是（ ）
A. -2 B. C. D. 2
【正确答案】B

【分析】根据倒数的定义求解．
【详解】解：-2的倒数是-，
故选：B．
本题难度较低，主要考查学生对倒数相反数等知识点的掌握．

2. 我国最长的河流长江全长约为6300千米，用科学记数法表示为（　　）
A. 63×102米 B. 6.3×103米 C. 6.3×106米 D. 6.3×105米
【正确答案】C

【详解】根据科学记数法的表示形式（a×10n，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的值与小数点移动的位数相同．当原数值＞1时，n是正数；当原数的值＜1时，n是负数）可得：
6300千米用科学记数法表示为6.3×106米，
故选C．
3. 单项式的系数与次数分别是（ ）
A. 3，4 B. -3，4 C. ，4 D. ，3
【正确答案】D

【分析】单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数，据此回答可得．
【详解】单项式的系数为、次数为
故D．
本题考查了单项式的系数和次数问题，掌握单项式的定义以及性质是解题的关键．
4. 下列计算正确的是（　　）
A. 3a+4=7ab B. 7x﹣3x=4
C. 3m+m=3m2 D. 3x2y﹣2x2y=x2y
【正确答案】D

【详解】解：A.3a与4没有是同类项，没有能合并，此选项错误；
B.7x﹣3x=4x，此选项错误；
C.3m+m=4m，此选项错误；
D.3x2y﹣2x2y=x2y，此选项正确；
故选D．
5. 如果x=1是关于x的方程﹣x+a=3x﹣2的解，则a的值为（　　）
A. 1 B. ﹣1 C. 2 D. ﹣2
【正确答案】C

详解】解： 把代入方程得到：，
解得．
故选C．
本题考查一元方程的解，难度没有大．
6. 将一副三角板按如图方式摆放在一起，且∠1比∠2大30°，则∠1的度数等于(　　)

A. B. C. D.
【正确答案】B

【分析】设出未知数：∠2=x，则∠1=x+30°，根据∠1和∠2的互余关系列出方程，解方程即可．
【详解】解：设∠2为x，则∠1=x+30°；
根据题意得：
x+x+30°=90°，
解得：x=30°，
则∠1=30°+30°=60°；
故选B．
本题考查了余角的定义；关键是设出未知数找出等量关系列方程．
7. 过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图正确的为（　　）

A. B. C. D.
【正确答案】B

【详解】试题解析：选项折叠后都没有符合题意，只有选项折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，与正方体三个剪去三角形交于一个顶点符合.
故选B.
8. 某品牌电脑降价15%后，每台售价a元，则这种电脑的原价为每台（　　）元．
A. 0.85a B. 0.15a C. D.
【正确答案】D

【详解】根据题意得，电脑的原价=a÷（1﹣15%）=元，
故选D．
9. 方程去分母正确的是（ ）.
A. x-1-x=-1 B. 4x-1-x=-4 C. 4x-1+x=-4 D. 4x-1+x=-1
【正确答案】C

【详解】
方程左右两边各项都要乘以4，故选C
10. 运用等式的性质变形，正确的是（ ）
A. 如果，那么 B. 如果，那么
C. 如果，那么 D. 如果那么
【正确答案】B

【分析】根据等式的基本性质进行判断即可．
【详解】如果，那么，故A错误；
如果，那么，故B正确；
如果，那么（c≠0），故C错误；
如果那么，故D错误．
故选：B
本题考查的是等式的基本性质，掌握等式的基本性质是关键，需要注意的是，在等式的两边除以一个相同的数（或代数式）时，这个数（或代数式）没有能为0．
11. 若2x﹣1=3y﹣2，则6y﹣4x的值是（　　）
A 1 B. ﹣1 C. 2 D. ﹣2
【正确答案】C

【详解】∵2x﹣1=3y﹣2，
∴3y﹣2x=﹣1+2=1
∴6y﹣4x=2（3y﹣2x）=2×1=2．
故选C．
解题关键是将6y﹣4x变形成含3y﹣2x形式.
12. 一组按规律排列的多项式： ，其中第10个式子是( )
A. B. C. D.
【正确答案】A

【分析】把已知的多项式看成由两个单项式组成，分别找出两个单项式的规律，也就知道了多项式的规律．
【详解】多项式的项依次是x，x2，x3，x4，…，xn，
第二项依次是y，-y3，y5，-y7，…，(-1)n+1y2n-1，
所以第10个式子即当n=10时，
代入到得到xn+(-1)n+1y2n-1=x10-y19．
故选：A．
本题主要考查了多项式，本题属于找规律的题目，把多项式分成几个单项式的和，分别找出各单项式的规律是解决这类问题的关键．
二、填 空 题（本大共1大题， 8小题，每小题3分共24分）
13. 若（m+3）2+|n﹣2|=0，则﹣mn=_____
【正确答案】﹣9．

【详解】∵（m+3）2+|n﹣2|=0，
∴m+3=0，n﹣2=0，
解得：m=﹣3，n=2，
则﹣mn=﹣（﹣3）2=﹣9．
故答案为﹣9．
14. 如果单项式3xa+2yb﹣2与5x3ya+2的和为8x3ya+2，那么a﹣b=_____．
【正确答案】﹣4．

【详解】∵单项式3xa+2yb﹣2与5x3ya+2的和为8x3ya+2，
∴a+3=3，b﹣2=a+2，
解得：a=0，b=4，
故a﹣b=﹣4．
故答案为﹣4．
15. 已知| x |= 8 ，| y |= 3，|x + y |=x+y ，则 x+y=___________.
【正确答案】5或11．

【分析】根据题意，利用值的代数意义确定出x与y的值，即可求出x+y的值．
【详解】∵|x|=8，|y|=3，∴x=±8，y=±3，
又|x+y|=x+y，即x+y≥0，∴x=8，y=3或x=8，y=﹣3．
①当x=8，y=3时，x+y=11；
②当x=8，y=﹣3时，x+y=5．
故5或11．
本题考查了有理数的加法，熟练掌握运算法则是解答本题的关键．
16. 若关于x的方程nxn﹣2﹣n+4=0为一元方程，则这个方程的解是____________．
【正确答案】x=-.

【详解】一元方程是指只含有一个未知数并且未知数的次数为1次的整式方程.本题根据定义可得：n+2=1，求出n的值，然后进行求解.
解：∵关于x的方程nxn-2-n+4=0为一元方程，
∴n-2=1，
解得：n=3，
故3x+1=0，
解得：x=-
故答案x=-.
17. 某校春游，若包租相同的大巴13辆，那么就有14人没有座位；如果多包租1辆，那么就多了26个空位，若设春游的总人数为x人，则列方程为_____
【正确答案】

【分析】设春游的总人数是x人，由包租相同的大巴13辆，有14人没有座位可得一辆大巴所坐的人数为人；由多包租1辆，就多了26个空位可得一辆大巴所坐的人数为人，由此即可得方程．
【详解】解：设春游的总人数是x人．
根据题意可列方程为： ，
故答案为．
本题考查了一元方程的应用，根据题意表示出一辆大巴所坐的人数是解决问题的关键.
18. 已知线段AB＝8cm，在直线AB上有一点C，且BC＝4cm，M是线段AC的中点，则线段AM的长为_____．
【正确答案】6cm或2cm##2cm或6cm

【详解】①当点C在线段AB的延长线上时，此时AC=AB+BC=12cm，
∵M是线段AC的中点，则AM=AC=6cm；
②当点C在线段AB上时，AC=AB﹣BC=4cm，
∵M是线段AC的中点，则AM=AC=2cm．
故答案为6cm或2cm．
19. 如果一个角的补角是150°，那么这个角的余角是_________°.
【正确答案】60

【分析】先根据补角的定义求出这个角，再根据余角的定义解答即可．
【详解】解：因为这个角的补角是150°，
所以这个角是30°，
所以这个角的余角是60°．
故60．
本题考查了补角和余角的定义，属于基础题型，熟练掌握基本知识是解题关键．
20. 如图，在1000个“〇”中依次填入一列数字m1，m2，m3…，m1000使得其中任意四个相邻“〇”中所填数字之和都等于﹣10，已知m25=x﹣1，m999=﹣2x，可得x的值为_____．

【正确答案】2

详解】∵a1+a2+a3+a4=a2+a3+a4+a5，a5+a6+a7+a8=a6+a7+a8+a9，…，
∴a1=a5=a9=…=x﹣1，
同理可得a2=a6=a10=…=﹣7，
a3=a7=a11=…=﹣2x，
a4=a8=a12=…=0，
∵a1+a2+a3+a4=﹣10，
∴﹣2x﹣7+x﹣1+0=﹣10，
解得：x=2．
故答案为2．
数字的变化规律：通过从一些的数字变化中发现没有变的因素或按规律变化的因素，然后推广到一般情况．
三、解 答 题
21. （1）计算 （﹣1）2×（﹣23）﹣（﹣4）÷2×
（2）先化简，再求值已知2（3a2b﹣5ab2）﹣3（2a2b﹣3ab2），其中a=﹣1，b=3．
（3）解方程：3（x﹣3）+1=x﹣（2x﹣1）
（4）解方程：﹣=2
【正确答案】（1）﹣7；（2）﹣ab2，9；（3）x=；（4）x=3．

【分析】（1）原式先计算乘方运算，再计算乘除运算，算加减运算即可求出值；
（2）原式去括号合并得到最简结果，把a与b的值代入计算即可求出值；
（3）方程去括号，移项合并，把x系数化为1，即可求出解；
（4）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
【详解】解：（1）原式=﹣8+1=﹣7；
（2）原式=6a2b﹣10ab2﹣6a2b+9ab2=﹣ab2，
当a=﹣1，b=3时，原式=9；
（3）去括号得：3x﹣9+1=x﹣2x+1，
移项合并得：4x=9，
解得：x=；
（4）去分母得：4x+2﹣x+1=12，
移项合并得：3x=9，
解得：x=3．
22. 如图，已知∠COB=2∠AOC，OD平分∠AOB，∠COD=10°，求∠AOB的度数．

【正确答案】∠AOB=60°．

【详解】试题分析：根据角平分线的性质得出∠AOD=∠BOD=∠AOB，则∠AOD=∠AOC，进而得出∠COD=∠AOD-∠AOC=∠AOC，即可得出答案．
试题解析：
∵OD平分∠AOB，
∴∠AOD=∠BOD=∠AOB，
又∵∠COB=2∠AOC，
∴∠AOD=∠AOC，
∴∠COD=∠AOD﹣∠AOC=∠AOC，
∵∠COD=10°，
∴∠AOC=20°，
∴∠AOB=3∠AOC=60°．
23. 如图，点在线段上，点分别是的中点．
（1）若，求线段MN 的长；
（2）若为线段上任一点，满足，其它条件没有变，你能求出的长度吗？请说明理由．
（3）若在线段的延长线上，且满足分别为 AC、BC的中点，你能求出的长度吗？请画出图形，写出你的结论，并说明理由．

【正确答案】（1）7.5；（2）a，理由见解析；（3）能，MN=b，画图和理由见解析

【分析】（1）据“点M、N分别是AC、BC的中点”，先求出MC、CN的长度，再利用MN=CM+CN即可求出MN的长度即可．
（2）据题意画出图形，利用MN=MC+CN即可得出答案．
（3）据题意画出图形，利用MN=MC-NC即可得出答案．
【详解】解：（1）点M、N分别是AC、BC的中点，
∴CM=AC=4.5cm，
CN=BC=3cm，
∴MN=CM+CN=4.5+3=7.5cm．
所以线段MN的长为7.5cm．
（2）MN的长度等于a，
根据图形和题意可得：MN=MC+CN=AC+BC=（AC+BC）=a；

（3）MN的长度等于b，
根据图形和题意可得：
MN=MC-NC=AC-BC=（AC-BC）=b．

本题主要考查了两点间的距离，关键是掌握线段的中点把线段分成两条相等的线段，注意根据题意画出图形也是关键．

24. （10分）下表是居民生活用气阶梯价格，
一般生活用气
　
户年天然气用量（m3）
价格
　
6口（含）以上
6口以下
档
0﹣500（含）
0﹣350（含）
2.28元/m3
第二档
500﹣650（含）
350﹣500（含）
2.5元/m3
第三档
650以上
500以上
3.9元/m3
（1）小明家6口人，2017年全年天然气用量为550m3，小明家需交多少费用？
（2）小华家5口人，2017年全年天然气共缴费1251元，请求出小华家2017年共用了多少m3天然气？
【正确答案】（1）小明家需交1265元；（2）小华家2017年共用了520m3天然气．

【分析】（1）根据6口之家生活用气阶梯价格，列式求值即可得出结论；
（2）设小华家共用了xm3天然气，先求出5口之家用气500m3的费用，与1251比较后可得出x超过500，再根据使用500m3天然气的费用+超出500m3的部分×3.9=应缴费用，即可得出关于x的一元方程，解之即可得出结论．
【详解】（1）根据题意得：500×2.28+（550﹣500）×2.5=1265（元）．
答：小明家需交1265元．
（2）解：设小华家共用了xm3天然气，
∵350×2.28+（500﹣350）×2.5=1173（元），1173＜1251，
∴x超过500．
根据题意得：1173+（x﹣500）×3.9=1251，
解得：x=520．
答：小华家2017年共用了520m3天然气．
25. 如图，OC在∠BOD内．
（1）如果∠AOC和∠BOD都是直角．
①若∠BOC=60°，则∠AOD的度数是　 　；
②猜想∠BOC与∠AOD的数量关系，并说明理由；
（2）如果∠AOC=∠BOD=x°，∠AOD=y°，求∠BOC的度数．

【正确答案】（1）①∠AOD=120°；②猜想∠BOC+∠AOD=180°，证明见解析；（2）120°．

【分析】（1）①根据直角的定义先求出∠AOB，再根据角的和差关系即可得出答案；
②得到∠AOD+∠BOC=∠BOD+∠AOC，代入求出即可；
（2）类比②可得：∠AOD+∠BOC=∠BOD+∠AOC，依此代入计算即可求解．
【详解】（1）①∵∠AOC和∠BOD都是直角，∠BOC=60°，
∴∠AOB=30°，
∴∠AOD=120°；
②猜想∠BOC+∠AOD=180°．
证明：∵∠BOC=90°，
∴∠AOD=∠BOD+∠AOB=90°+∠AOB，
∵∠AOC=90°，
∴∠AOD+∠BOC=∠BOD+∠AOC=90°+90°=180°；
（2）类比②可得：∠AOD+∠BOC=∠BOD+∠AOC，
∵∠BOD=∠AOC=x°，∠AOD=y°，
∴∠BOC=（2x﹣y）°．
故答案为120°．
考查了角的有关计算，主要考查学生根据图形进行计算的能力，题目比较好，但有一定的难度．