

2022-2023学年北京市海淀区九年级上册数学期末专项提升模拟卷(AB卷)含解析
展开1. 下列平面图形中,既是轴对称图形,又是对称图形的是( )
A. B. C. D.
2. 一圆的半径为3,圆心到直线的距离为4,则该直线与圆的位置关系是( )
A. 相切B. 相交C. 相离D. 以上都没有对
3. 一元二次方程x2-3x+2=0 的两根分别是x1、x2,则x1+x2的值是( )
A. 3B. 2C. -3D. -2
4. 已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A. 2B. 4C. 6D. 8
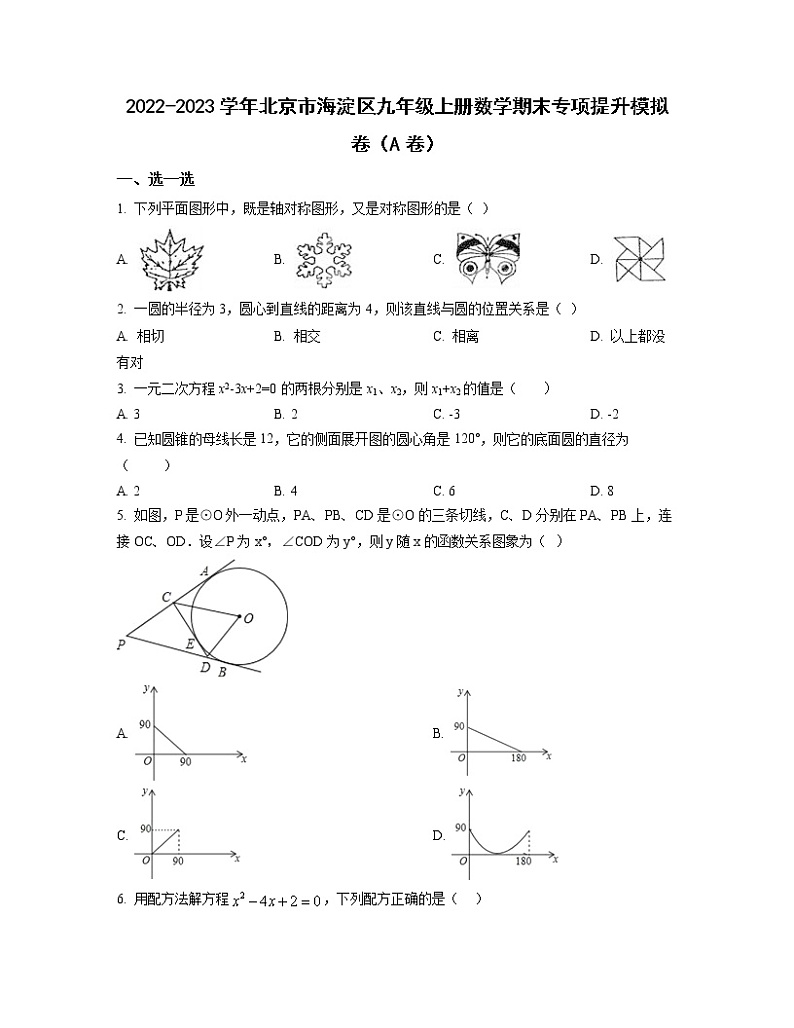
5. 如图,P是⊙O外一动点,PA、PB、CD是⊙O的三条切线,C、D分别在PA、PB上,连接OC、OD.设∠P为x°,∠COD为y°,则y随x的函数关系图象为( )
A. B.
C. D.
6. 用配方法解方程,下列配方正确的是( )
A. B. C. D.
7. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(没有包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④<a<⑤b>c.其中含所有正确结论的选项是( )
A. ①③B. ①③④C. ②④⑤D. ①③④⑤
8. 二次函数y=+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
则该函数图象的对称轴是( ).
A. 直线x=﹣3B. 直线x=﹣2
C. 直线x=﹣1D. 直线x=0
9. 端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只干肉粽,粽子除内部馅料没有同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是( )
A. B. C. D.
10. 如图,某小区在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2,若设通道的宽度为x(m),则根据题意所列的方程是( )
A. (40﹣x)(26﹣2x)=144×6B. (40﹣2x)(26﹣x)=144×6
C. (40﹣2x)(26﹣x)=144÷6D. (40﹣x)(26﹣2x)=144÷6
二、填 空 题
11. 如图,AB是⊙O一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的值为_______.
12. 已知一包糖果共有5种颜色(糖果只有颜色差别),如图是这包糖果分布百分比的统计图,在这包糖果中任意取一粒,则取出糖果的颜色为绿色或棕色的概率是_________.
13. 如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
14. 若m,n是一元二次方程+x-2015=0的两个实数根,则m2+2m+n的值为________
15. 圆内接正六边形的边心距为2,则这个正六边形的面积为_____cm2.
16. 二次函数y=-6x2,当x1>x2>0时,y1与y2的大小关系为____.
三、解 答 题
17. 一没有透明布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(没有放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
18. 抛物线与轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C没有重合),连接AP交y轴于点N,连接BC和PC.
(1)时,求抛物线的解析式和BC的长;
(2)如图时,若AP⊥PC,求的值;
(3)是否存在实数,使,若存在,求出值;若没有存在,请说明理由.
19. 如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
(1)求证:△ABC等边三角形;
(2)若∠PAC=90°,AB=,求PD的长.
20 解方程:(1);(2)
21. 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE
(Ⅰ)求证:AE是⊙O的切线;
(Ⅱ)若∠DBC=30°,DE=1 cm,求BD的长.
22. 某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为W元,当每个房间定价为多少元时,宾馆每天所获利润,利润是多少;
(3)某日,宾馆了解当天的住宿情况,得到以下信息:
①当日所获利润没有低于5000元,
②宾馆为游客居住的房间共支出费用没有超过600元,
③每个房间刚好住满2人.
问:这天宾馆入住的游客人数至少有多少人.
23. 如图,在等边△ABC中,D是AC边上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9,则△AED的周长是______.
2022-2023学年北京市海淀区九年级上册数学期末专项提升模拟卷(A卷)
一、选一选
1. 下列平面图形中,既是轴对称图形,又是对称图形的是( )
A. B. C. D.
【正确答案】B
【详解】AC是轴对称图形,沿中间轴对称,但没有是对称图形,因为AC转180°没有能和原来的图形重合;D是对称图形但没有是轴对称图形;B既是对称图形也是对称图形.
2. 一圆的半径为3,圆心到直线的距离为4,则该直线与圆的位置关系是( )
A. 相切B. 相交C. 相离D. 以上都没有对
【正确答案】C
【详解】∵由题意可知d="4,r=3,
∴d>r.
∴直线与圆相离.
故选C.
3. 一元二次方程x2-3x+2=0 的两根分别是x1、x2,则x1+x2的值是( )
A. 3B. 2C. -3D. -2
【正确答案】A
【详解】解:x2-3x+2=0
a=1,b=-3,
则x1+x2=-=3,
故选:A.
本题考查一元二次方程根与系数的关系.
4. 已知圆锥母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A. 2B. 4C. 6D. 8
【正确答案】D
【分析】根据圆锥侧面展开图的圆心角与半径(即圆锥的母线的长度)求得的弧长,就是圆锥的底面的周长,然后根据圆的周长公式l=2πr解出r的值即可.
【详解】试题解析:设圆锥的底面半径为r
圆锥的侧面展开扇形的半径为12,
∵它的侧面展开图的圆心角是
∴弧长 即圆锥底面的周长是
解得,r=4,
∴底面圆的直径为8.
故选:D.
本题考查了圆锥的计算.正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
5. 如图,P是⊙O外一动点,PA、PB、CD是⊙O的三条切线,C、D分别在PA、PB上,连接OC、OD.设∠P为x°,∠COD为y°,则y随x的函数关系图象为( )
A. B.
C. D.
【正确答案】B
【详解】试题解析:设CD与⊙O相切于点E,连结OA、OB、OE,如图,
∵PA、PB、CD是⊙O的三条切线,
∵CA=CE,DE=DB,OA⊥PA,OB⊥PB,OE⊥CD,
∴OC平分∠AOE,OD平分∠BOE,
∴∠1=∠2,∠3=∠4,
∴∠COD=∠2+∠3=∠AOB,
∵∠AOB=180°﹣∠P=180°﹣x°,
∴y=90°﹣x(0<x<180°).
故选B.
考点:动点问题的函数图象.
6. 用配方法解方程,下列配方正确的是( )
A. B. C. D.
【正确答案】D
【分析】先移项,再利用完全平方公式进行配方即可得.
【详解】解:,
,
,
,
故选:D.
本题考查了利用配方法解一元二次方程,熟记完全平方公式是解题关键.
7. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(没有包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④<a<⑤b>c.其中含所有正确结论的选项是( )
A. ①③B. ①③④C. ②④⑤D. ①③④⑤
【正确答案】D
【详解】①∵函数开口方向向上,∴a>0;∵对称轴在y轴右侧,∴ab异号,∵抛物线与y轴交点在y轴负半轴,∴c<0,∴abc>0,故①正确;
②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=1,∴图象与x轴的另一个交点为(3,0),∴当x=2时,y<0,∴4a+2b+c<0,故②错误;
③∵图象与x轴交于点A(﹣1,0),∴当x=﹣1时,y==0,∴a﹣b+c=0,即a=b﹣c,c=b﹣a,∵对称轴为直线x=1,∴=1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴4ac﹣=4•a•(﹣3a)﹣=<0,∵8a>0,∴4ac﹣<8a,故③正确;④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1,∴﹣2<﹣3a<﹣1,∴>a>,故④正确;⑤∵a>0,∴b﹣c>0,即b>c,故⑤正确.
故选D.
本题考查二次函数的图像与系数的关系,熟练掌握图像与系数的关系,数形来进行判断是解题的关键.
8. 二次函数y=+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
则该函数图象的对称轴是( ).
A. 直线x=﹣3B. 直线x=﹣2
C 直线x=﹣1D. 直线x=0
【正确答案】B
【详解】根据二次函数图像的对称性,可知其对称轴为x=-2.
故选B.
点睛:此题主要考查了二次函数的图像与性质,利用二次函数的图像表示法,确定其对称轴,关键是确定其中的一对对称点,进而计算出对称轴.
9. 端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽、3只碱水粽、5只干肉粽,粽子除内部馅料没有同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是( )
A. B. C. D.
【正确答案】B
【详解】解:根据概率的定义,一共有10只粽子,其中红豆粽有2个,
所以吃到红豆粽的概率是.
故选B.
10. 如图,某小区在一个长AD=40m,宽AB=26m矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2,若设通道的宽度为x(m),则根据题意所列的方程是( )
A. (40﹣x)(26﹣2x)=144×6B. (40﹣2x)(26﹣x)=144×6
C. (40﹣2x)(26﹣x)=144÷6D. (40﹣x)(26﹣2x)=144÷6
【正确答案】B
【详解】设通道的宽度为x(m),
根据题意得(40﹣2x)(26﹣x)=144×6,
故选:B.
二、填 空 题
11. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的值为_______.
【正确答案】10.5
【详解】如图,连接OA,OB,
∵∠ACB=30°,∴∠AOB=60°.
∵OA=OB,∴△OAB是等边三角形.∴OA=OB=AB=7.
∵E、F是AC、BC的中点,∴EF==3.5.
∵GE+FH=GH-EF,EF为定值,∴要使GE+FH,即要GH.
∴当GH为直径时,GE+FH的值为14-3.5=10.5.
12. 已知一包糖果共有5种颜色(糖果只有颜色差别),如图是这包糖果分布百分比的统计图,在这包糖果中任意取一粒,则取出糖果的颜色为绿色或棕色的概率是_________.
【正确答案】
【分析】先求出棕色所占的百分比,再根据概率公式列式计算即可得解.
【详解】解:棕色所占的百分比为:1﹣20%﹣15%﹣30%﹣15%=1﹣80%=20%,
所以,P(绿色或棕色)=30%+20%=50%=.
故.
本题考查了概率的知识.用到的知识点为:概率=所求情况数与总情况数之比.
13. 如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
【正确答案】17°
【详解】解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50°−33°=17°.
故答案为17°.
14. 若m,n是一元二次方程+x-2015=0的两个实数根,则m2+2m+n的值为________
【正确答案】2014
【详解】试题分析:根据韦达定理可得:m+n=-1;将x=m代入方程可得:+m=2015,则原式=+m+m+n=2015+(-1)=2014.
考点:(1)、一元二次方程的解;(2)、韦达定理
15. 圆内接正六边形的边心距为2,则这个正六边形的面积为_____cm2.
【正确答案】.
【详解】试题分析:因为圆内接正六边形的两条半径与正六边形边长组成等边三角形,由边心距可求得正六边形的边长是,把正六边形分成6个这样的三角形,则这个正六边形的面积为4×÷2×6=.
考点:圆内接正多边形面积计算.
16. 二次函数y=-6x2,当x1>x2>0时,y1与y2的大小关系为____.
【正确答案】y1<y2
【详解】试题分析:由函数的解析式可知a=-6,函数的开口线下,在x>0时,y随x增大而减小,因此可知当x1>x2>0时,y1<y2.
故答案为 y1<y2
三、解 答 题
17. 一没有透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(没有放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球概率;
【正确答案】(1)1;(2)
【分析】(1)设口袋中黄球的个数为x个,根据从中任意摸出一个球是红球的概率为和概率公式列出方程,解方程即可求得答案;(2)根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出都是红球的情况,再利用概率公式即可求得答案;
【详解】解:(1)设口袋中黄球的个数为个,
根据题意得:
解得:=1
经检验:=1是原分式方程的解
∴口袋中黄球的个数为1个
(2)画树状图得:
∵共有12种等可能的结果,两次摸出都是红球的有2种情况
∴两次摸出都是红球的概率为: .
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以没有重复没有遗漏的列出所有可能的结果,列表法适合于两步完成的,树状图法适合两步或两步以上完成的.
18. 抛物线与轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C没有重合),连接AP交y轴于点N,连接BC和PC.
(1)时,求抛物线的解析式和BC的长;
(2)如图时,若AP⊥PC,求的值;
(3)是否存在实数,使,若存在,求出的值;若没有存在,请说明理由.
【正确答案】(1),BC=2;(2);(3).
【详解】试题分析:(1)由抛物线与轴相交于O、A两点(其中O为坐标原点),得到b=0,故抛物线为,把代入,得到P(2,3)和,由对称轴x=2,即可得到BC的长;
(2)把x=2代入,得到B(2,),设C(x, ),由对称轴,得到C(, ),由,得到A(4a,0),由AP⊥PC,得到,即,解方程即可得到结论;
(3)由OA=4a, OM=2,得到AM=4a-2,由PM∥ON,得到, 即,解方程即可得到结论.
试题解析:(1)∵抛物线与轴相交于O、A两点(其中O为坐标原点),∴b=0,∴,当时,P(2,3),,∴=,∴对称轴为:x=2,∴BC=2×(3-2)=2;
(2)当x=2时,=,∴B(2,),设C(x, ),∵对称轴,∴,∴,∴C(, ),∵,∴A(4a,0),∵AP⊥PC,∴,∴,整理得:,解得:,∵,∴;
(3)∵A(4a,0),∴OA=4a,∵P(2,2a),∴OM=2,∴AM=4a-2,∵PM∥ON,∴, ∴,解得:.
考点:二次函数综合题;存在型;综合题.
19. 如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=,求PD的长.
【正确答案】(1)见解析;(2)4.
【详解】试题分析:(1)由圆周角定理可知∠ABC=∠BAC=60°,从而可证得△ABC等边三角形;
(2)由△ABC是等边三角形可得出“AC=BC=AB=,∠ACB=60°”,在直角三角形PAC和DAC通过角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.
试题解析:(1)∵∠ABC=∠APC,∠BAC=∠BPC,∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC是等边三角形;
(2)∵△ABC是等边三角形,AB=,∴AC=BC=AB=,∠ACB=60°.在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=,∴AP=AC•ct∠APC=2.在Rt△DAC中,∠DAC=90°,AC=,∠ACD=60°,∴AD=AC•tan∠ACD=6,∴PD=AD﹣AP=6﹣2=4.
考点:四点共圆;等边三角形的判定与性质;圆周角定理.
20. 解方程:(1);(2)
【正确答案】(1),;(2),
【详解】(1) (2)
解: 解:
21. 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE
(Ⅰ)求证:AE是⊙O的切线;
(Ⅱ)若∠DBC=30°,DE=1 cm,求BD的长.
【正确答案】(Ⅰ)见解析;(Ⅱ)4.
【详解】(Ⅰ)证明:连结OA,
∵DA平分∠BDE,
∴∠ADE=∠ADO ,
∵OA=OD,
∴∠OAD=∠ADO ,
∴∠ADE=∠OAD,
∴OA∥CE,
∵AE⊥CD,
∴AE⊥OA,
∴AE是⊙O的切线;
(Ⅱ)∵BD是⊙O的直径,
∴∠BCD=90°,
∵∠DBC=30°,
∴∠BDE=120°,
∵DA平分∠BDE,
∴∠ADE=∠ADO=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=BD,
在Rt△AED中,DE=1,∠ADE=60°,
∴AD== 2,
∴BD=4.
22. 某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为W元,当每个房间定价为多少元时,宾馆每天所获利润,利润是多少;
(3)某日,宾馆了解当天的住宿情况,得到以下信息:
①当日所获利润没有低于5000元,
②宾馆为游客居住的房间共支出费用没有超过600元,
③每个房间刚好住满2人.
问:这天宾馆入住的游客人数至少有多少人.
【正确答案】(1)y=50-x,(0≤x≤50,且x为整数);(2)每间房价定价为320元时,宾馆每天所获利润,利润是9000元;(3)20人.
【详解】试题分析:(1)根据每天游客居住的房间数量等于50﹣减少的房间数即可解决问题.
(2)构建二次函数,利用二次函数的性质解决问题.
(3)根据条件列出没有等式组即可解决问题.
试题解析:(1)根据题意,得:y=50﹣x,(0≤x≤50,且x为整数);
(2)W=(120+10x﹣20)(50﹣x)=
∵a=﹣10<0,∴当x=20时,W取得值,W值=9000元.
答:当每间房价定价为320元时,宾馆每天所获利润,利润是9000元;
(3)由,解得20≤x≤40.
当x=40时,这天宾馆入住的游客人数至少,至少人数为2y=2(﹣x+50)=20(人).
考点:1.二次函数的应用;2.一元没有等式组的应用;3.二次函数的最值;4.最值问题.
23. 如图,在等边△ABC中,D是AC边上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9,则△AED的周长是______.
【正确答案】19.
【详解】解:∵将△BCD绕点B逆时针旋转60°得到△BAE
∴△BDC≌△BAE
∴BE=BD,∠DBE=60°,AE=CD
∴△DBE是等边三角形
∴DE=BD=9
∴△AED的周长=DE+AD+AE=DE+AC=19
故19
2022-2023学年北京市海淀区九年级上册数学期末专项提升模拟卷(B卷)
一、选一选
1. 同时投掷两枚硬币,出现两枚都是正面朝上的概率是( )
A. B. C. 1D.
2. 抛物线y=x2﹣2x向右平移2个单位再向上平移3个单位,所得图象的解析式为( )
A. y=x2+3B. y=x2﹣4x+3C. y=x2﹣6x+11D. y=x2﹣6x+8
3. 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有( )
A. a>0,b>0B. a>0,c>0C. b>0,c>0D. a,b,c都小于0
4. 若没有等式组 (x为未知数)无解,则二次函数的图象y=ax2﹣2x+1与x轴的交点( )
A. 没有交点B. 一个交点C. 两个交点D. 没有能确定
5. 函数与在同一直角坐标系中的大致图象可能是( )
A. B. C. D.
6. 如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
A. 6B. 12C. 15D. 30
7. 若关于x的方程x2-x+csα=0有两个相等的实数根,则锐角α为( ).
A. 30°B. 45°C. 60°D. 75°
8. 关于x的一元二次方程x2-4x+(5-m)=0有实数根,则m的取值范围是( )
A. m>1B. m≥1C. m<1D. m≤1
9. 一元二次方程x2﹣x﹣1=0和2x2﹣6x+5=0,这两个方程的所有实数根之和为( )
A 4B. ﹣4C. ﹣6D. 1
10. 有两个一元二次方程:①,②,其中a+c=0,
以下四个结论中,错误的是( )
A. 如果方程①有两个相等的实数根,那么方程②也有两个相等的实数根;
B. 如果方程①和方程②有一个相同实数根,那么这个根必定是x=1;
C. 如果4是方程①的一个根,那么是方程②的一个根;
D. 方程①的两个根的符号相异,方程②的两个根的符号也相异;
二、填 空 题
11. 方程x2=2x的解是_______.
12. 已知直角三角形两条直角边长分别为5、12,则它的外接圆半径R=______ .
13. 已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为,将△ADE按顺时针方向旋转得△ABF,则点E所的路径长为___________cm.
14. 如图,内接于,于点,,,,则的直径是________.
15. 如图,要拧开一个边长为6cm的正六边形螺帽,扳手张开的开口a至少为________cm.
16. 函数y=﹣x+4图象与x轴、y轴分别交于点A、点B,点P为正比例函数y=kx(k>0)图象上一动点,且满足∠PBO=∠POA,则AP的最小值为_____.
三、解 答 题
17. 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所的路径长(记过保留根号和π).
18. 如图,已知在中,,是的平分线.
(1)作一个使它两点,且圆心在边上;(没有写作法,保留作图痕迹)
(2)判断直线与的位置关系,并说明理由.
19. 解下列方程:(1). (2)x2+4x-1=0.
20. 某商场一批衬衫,平均每天可售出件,每件盈利元,为了扩大,增加盈利,尽快减少库存,商场决定采取适当的减价措施,经发现,如果每件衬衫每降元,商场平均每天可多售出件.若商场平均每天要盈利元,每件衬衫应降价多少元?这时应进货多少件?
21. 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(没有含端点A、D),连结BE、CE.
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
22. 关于x的一元二次方程有两个没有等实根.
(1)求实数k的取值范围.
(2)若方程两实根满足,求k的值.
23. 如图,抛物线C1:y=x2+bx+c原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2,C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△PAC为等边三角形,求m的值.
2022-2023学年北京市海淀区九年级上册数学期末专项提升模拟卷(B卷)
一、选一选
1. 同时投掷两枚硬币,出现两枚都是正面朝上的概率是( )
A. B. C. 1D.
【正确答案】B
【详解】试题解析:根据题意画树状图如下:
∵共有4种等可能的结果,两枚都出现正面朝上的有1种情况,
∴两枚都出现正面朝上的概率是
故选B.
2. 抛物线y=x2﹣2x向右平移2个单位再向上平移3个单位,所得图象的解析式为( )
A. y=x2+3B. y=x2﹣4x+3C. y=x2﹣6x+11D. y=x2﹣6x+8
【正确答案】C
【分析】
【详解】解:二次函数y=x2﹣2x=(x﹣1)2﹣1的图象的顶点坐标是(1,﹣1),
则向右平移2个单位再向上平移3个单位后的函数图象的顶点坐标是(3,2).
则所得抛物线解析式为:y=(x﹣3)2+2=x2﹣6x+11.
故选C.
考点:二次函数图象与几何变换.
3. 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有( )
A. a>0,b>0B. a>0,c>0C. b>0,c>0D. a,b,c都小于0
【正确答案】C
【详解】试题分析:根据函数图象可以得到以下信息:a<0,b>0,c>0,再函数图象判断各选项.
解:由函数图象可以得到以下信息:a<0,b>0,c>0,
A、错误;B、错误;C、正确;D、错误;
故选C.
考点:二次函数图象与系数的关系.
4. 若没有等式组 (x为未知数)无解,则二次函数的图象y=ax2﹣2x+1与x轴的交点( )
A. 没有交点B. 一个交点C. 两个交点D. 没有能确定
【正确答案】A
【详解】解:∵没有等式组(x为未知数)无解,
∴由
解得:
则x>a时此没有等式组无解,
∴
中,
∴二次函数的图象与x轴的没有交点.
故选A.
5. 函数与在同一直角坐标系中的大致图象可能是( )
A. B. C. D.
【正确答案】B
【分析】本题可先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.
【详解】解:由解析式y=-kx2+k可得:抛物线对称轴x=0;
A、由双曲线的两支分别位于二、四象限,可得k<0,则-k>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上,而没有是交于y轴正半轴,故选项A错误;
B、由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象符合题意,故选项B正确;
C、由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,而没有是y轴的负半轴,本图象没有符合题意,故选项C错误;
D、由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,而没有是开口向上,本图象没有符合同意,故选项D错误.
故选B.
本题考查二次函数及反比例函数和图象,解决此类问题步骤一般为:(1)先根据图象的特点判断k取值是否矛盾;(2)根据二次函数图象判断抛物线与y轴的交点是否符合要求.
6. 如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
A. 6B. 12C. 15D. 30
【正确答案】A
【详解】试题分析: ∵OD⊥BC,
∴BD=CD=BC=×12=6,
在Rt△BOD中,∵OB=AB=8,BD=6,
∴OD==2,
∴S△OBD=OD•BD=×2×6=6.
考点:垂径定理;勾股定理.
7. 若关于x的方程x2-x+csα=0有两个相等的实数根,则锐角α为( ).
A. 30°B. 45°C. 60°D. 75°
【正确答案】C
【详解】因为关于x的方程x2−2√x+csα=0有两个相等的实数根,
∴△=0,即(−)²−4×1×csα=0,
∴csα=,∴α=60°.
故选C.
8. 关于x一元二次方程x2-4x+(5-m)=0有实数根,则m的取值范围是( )
A. m>1B. m≥1C. m<1D. m≤1
【正确答案】B
【详解】∵方程x²−4x+(5−m)=0有实数根,
∴b²−ac=(−4) ²−4(5−m)⩾0,
解得:m⩾1.
故选B.
9. 一元二次方程x2﹣x﹣1=0和2x2﹣6x+5=0,这两个方程的所有实数根之和为( )
A. 4B. ﹣4C. ﹣6D. 1
【正确答案】D
【详解】∵在方程x2﹣x﹣1=0中,△=(﹣1)2﹣4×1×(﹣1)=5>0,
∴方程x2﹣x﹣1=0有两个没有相等的实数根,
设方程x2﹣x﹣1=0的两个根分别为m、n,
∴m+n=1.
∵在方程2x2﹣6x+5=0中,△=(﹣6)2﹣4×2×5=﹣4<0,
∴方程2x2﹣6x+5=0没有实数根.
∴一元二次方程x2﹣x﹣1=0和2x2﹣6x+5=0的所有实数根之和为1.
故选D.
10. 有两个一元二次方程:①,②,其中a+c=0,
以下四个结论中,错误的是( )
A. 如果方程①有两个相等的实数根,那么方程②也有两个相等的实数根;
B. 如果方程①和方程②有一个相同的实数根,那么这个根必定是x=1;
C. 如果4是方程①的一个根,那么是方程②的一个根;
D. 方程①的两个根的符号相异,方程②的两个根的符号也相异;
【正确答案】B
【详解】选项A,因为两个判别式一致,所以A对.
选项B,因为将1代入方程,值相等,B对.
选项C,因为16a+4b+c=0,
选项D,
所以选B.
二、填 空 题
11. 方程x2=2x的解是_______.
【正确答案】x1=0,x2=2
【分析】先移项得到x2﹣2x=0,再把方程左边进行因式分解得到x(x﹣2)=0,方程转化为两个一元方程:x=0或x﹣2=0,即可得到原方程的解为x1=0,x2=2.
【详解】解:∵x2﹣2x=0,
∴x(x﹣2)=0,
∴x=0或x﹣2=0,
∴x1=0,x2=2.
故x1=0,x2=2.
本题主要考查了解一元二次方程,熟练掌握一元二次方程的解法,并能够根据方程的特征灵活选用合适的方法解答是解题的关键.
12. 已知直角三角形的两条直角边长分别为5、12,则它的外接圆半径R=______ .
【正确答案】6.5
【详解】试题分析:因为直角三角形的两直角边长分别为5和12,所以斜边=13,所以它的外接圆的半径R=.
考点:勾股定理、直角三角形的外接圆.
13. 已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为,将△ADE按顺时针方向旋转得△ABF,则点E所的路径长为___________cm.
【正确答案】
【详解】解:∵四边形ABCD是正方形,
∴∠BAD=90°,
根据旋转的性质可得:∠EAF=90°,
∵AD=12cm,DE=5cm,
∴,
∴点E所的路径长为
故答案是:.
14. 如图,内接于,于点,,,,则的直径是________.
【正确答案】6cm.
【详解】试题分析:作⊙O的直径AE,连CE,如图,∵AE为直径,∴∠ACE=90°,又∵∠E=∠B,∴Rt△AEC∽Rt△ABD,∴,而AD=2cm,AB=4cm,AC=3cm,∴AE==×4cm=6cm.所以⊙O的直径是6cm.故答案为6cm.
考点:1.相似三角形的判定与性质;2.圆周角定理.
15. 如图,要拧开一个边长为6cm的正六边形螺帽,扳手张开的开口a至少为________cm.
【正确答案】
【分析】根据题意,即是求该正六边形的边心距的2倍,构造一个由半径、边长的一半、边心距组成的直角三角形,再根据锐角三角函数的知识求解即可.
【详解】解:设正多边形的是O,其一边是AB,AC与BO相交于点M,
∴∠AOB=∠BOC=60°,
∴OA=OB=AB=OC=BC,
∴四边形ABCO菱形,
∵OA=AB=6cm,∠AOB=60°,
∴∠OAC=30°,cs∠OAC=,
∴AM=6×=(cm),
∵OA=OC,且∠AOB=∠BOC,
∴AM=MC=AC,
∴AC=2AM=6(cm).
故答案为6.
本题考查了正多边形和圆的知识,构造一个由半径、半边和边心距组成的直角三角形、熟练掌握锐角三角函数的知识是解题的关键.
16. 函数y=﹣x+4图象与x轴、y轴分别交于点A、点B,点P为正比例函数y=kx(k>0)图象上一动点,且满足∠PBO=∠POA,则AP的最小值为_____.
【正确答案】2﹣2
【详解】如图所示:
因为∠PBO=∠POA,
所以∠BPO=90°,则点P是以OB为直径的圆上.
设圆心为M,连接MA与圆M的交点即是P,此时PA最短,
∵OA=4,OM=2,
∴MA=
又∵MP=2,AP=MA-MP
∴AP=.
三、解 答 题
17. 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所的路径长(记过保留根号和π).
【正确答案】(1)作图见试题解析,A1(2,﹣4);(2)作图见试题解析;(3).
【分析】(1)找到点A、B、C的对应点A1、B1、C1的位置,然后描点即可得到△A1B1C1;
(2)利用网格特点和旋转的性质,画出点A、C的对应点A2、C2,则可得到△A2BC2;
(3)C点旋转到C2点所的路径是以B点为圆心,BC为半径,圆心角为90°的弧,然后根据弧长公式计算即可.
【详解】解:(1)如图,△A1B1C1为所作,点A1的坐标为(2,﹣4);
(2)如图,△A2BC2为所作;
(3)BC==,所以C点旋转到C2点所的路径长=.
本题考查了作图﹣旋转变换,轴对称变换,勾股定理及弧长公式,解题的关键是能够准确找出对应点.
18. 如图,已知在中,,是的平分线.
(1)作一个使它两点,且圆心在边上;(没有写作法,保留作图痕迹)
(2)判断直线与的位置关系,并说明理由.
【正确答案】(1)见解析;(2)与相切,理由见解析.
【分析】(1)作出AD的垂直平分线,交AB于点O,进而利用AO为半径求出即可;
(2)利用半径相等角平分线的性质得出OD∥AC,进而求出OD⊥BC,进而得出答案.
【详解】(1)①分别以为圆心,大于的长为半径作弧,两弧相交于点和,
②作直线,与相交于点,
③以为圆心,为半径作圆,如图即为所作;
(2)与相切,理由如下:
连接OD,
为半径,
,
是等腰三角形,
,
平分,
,
,
,
,
,
,
为半径,
与相切.
本题主要考查了切线的判定以及线段垂直平分线的作法与性质等知识,掌握切线的判定方法是解题关键.
19. 解下列方程:(1). (2)x2+4x-1=0.
【正确答案】(1)x=5;(2) .
【详解】试题分析:(1)方程两边同时乘以(x-3)(x-2)去分母后,解一元方程,再解方程,验根即可;(2)首先把方程移项变形为x2+4x=1的形式,然后在方程的左右两边同时加上项系数一半的平方,左边就是完全平方式,右边就是常数,然后利用平方根的定义即可求解.
试题解析:
(1)2(x-2)=3(x-3)
2x-4=3x-9
2x-3x=-9+4
-x=-5
x=5
当x=5时,x-3≠0,x-2≠0
所以x=5是方程的解.
(2)x2+4x-1=0,
移项得,x2+4x=1,
配方得,x2+4x+4=1+4,
(x+2)2=5,
开方得,x+2=±
解得 ,
20. 某商场一批衬衫,平均每天可售出件,每件盈利元,为了扩大,增加盈利,尽快减少库存,商场决定采取适当的减价措施,经发现,如果每件衬衫每降元,商场平均每天可多售出件.若商场平均每天要盈利元,每件衬衫应降价多少元?这时应进货多少件?
【正确答案】每件衬衫应降价元,进货件.
【分析】利用衬衣平均每天售出的件数×每件盈利=每天这种衬衣利润列出方程解答即可.
【详解】设每件衬衫应降价x元.
根据题意,得(44−x)(20+5x)=1600,
解得x1=4,x2=18.
∵“扩大量,减少库存”,
∴x1=4应略去,
∴x=18.
20+5x=110.
答:每件衬衫应降价18元,进货110件.
考查了一元二次方程的应用,读懂题目,找出题目中的等量关系,列出方程是解题的关键.
21. 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(没有含端点A、D),连结BE、CE.
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
【正确答案】(1) b=12;(2);(3)见解析.
【详解】试题分析:(1)在矩形ABCD中,得到∠ABC=90°,利用勾股定理即可计算出结果.
(2)由∵BE⊥AC得到∠2+∠3=90°,由于∠1+∠3=90°,等量代换得到∠1=∠2,推出得到比例式,即可得到结论;
(3)点在线段上的任一点,且没有与重合,当与相似时,则当(如图2),又由平行线的性质得到推出得到比例式,进而可得得到一元二次方程根据方程根的情况,得到结论.
试题解析:(1)∵四边形ABCD是矩形,
∵AB=a=5, AC=13,
∴b=12;
如图1,∵BE⊥AC
又
∴∠1 = ∠2,
又
∴△AEB ∽△BAC
∴即,
∴.
(3)∵点E在线段AD上的任一点,且没有与A、D重合,
∴当△ABE与△BCE相似时,则
所以当△BAE ∽△CEB(如图2)
则∠1 = ∠BCE,
又BC∥AD,
∴∠2 = ∠BCE,
∴∠1 = ∠2 ,
又
∴△BAE ∽△EDC,
∴ 即 ,
∴ ,
即 ,
当 ,
∵a>0,b>0, ∴
即 时,
综上所述:当a、b满足条件b = 2a时△BAE ∽△CEB,此时 (或x = a);
当a、b满足条件b>2a时△BAE ∽△CEB,此时.
22. 关于x的一元二次方程有两个没有等实根.
(1)求实数k的取值范围.
(2)若方程两实根满足,求k的值.
【正确答案】(1)k﹥;(2)k=2
【分析】(1)根据方程有两个没有相等的实数根可得△>0,代入求得k的取值范围即可;(2)首先判断出两根均小于0,然后去掉值,进而得到,k的取值范围解方程即可.
【详解】解:(1)∵原方程有两个没有相等的实数根
∴
解得:k﹥;
故k﹥.
(2)∵k﹥,
∴<0
又∵
∴ ,
∴,
∵,
∴2k+1=k2+1,
解得:k1=0,k2=2
又 ∵k﹥
∴k=2.
故k=2.
23. 如图,抛物线C1:y=x2+bx+c原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2,C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△PAC为等边三角形,求m的值.
【正确答案】(1)抛物线C1的解析式为y=x2﹣2x,顶点坐标(1,﹣1);
(2)抛物线C2的解析式为:y=(x﹣2)2﹣1;
(3)m=.
【详解】试题分析:(1)把(0,0)及(2,0)代入y=x2+bx+c,求出抛物线C1的解析式,即可求出抛物线C1的顶点坐标,
(2)先求出C2的解析式,确定A,B,C的坐标,过点C作CH⊥对称轴DE,垂足为H,利用△PAC为等腰直角三角形,求出角的关系可证得△CHD≌△DEA,再由OC=EH列出方程求解得出m的值,即可得出C2的解析式.
(3)连接BC,BP,由抛物线对称性可知AP=BP,由△PAC为等边三角形,可得AP=BP=CP,∠APC=60°,由C,A,B三点在以点P为圆心,PA为半径的圆上,可得BC=2OC,利用勾股定理求出OB=OC,列出方程求出m的值即可.
试题解析:(1)∵抛物线C1原点,与x轴另一个交点为(2,0),
∴,
解得,
∴抛物线C1的解析式为y=x2﹣2x,
∴抛物线C1的顶点坐标(1,﹣1),
(2)如图1,
∵抛物线C1向右平移m(m>0)个单位得到抛物线C2,
∴C2的解析式为y=(x﹣m﹣1)2﹣1,
∴A(m,0),B(m+2,0),C(0,m2+2m),
过点C作CH⊥对称轴DE,垂足为H,
∵△ACD为等腰直角三角形,
∴AD=CD,∠ADC=90°,
∴∠CDH+∠ADE=90°
∴∠HCD=∠ADE,
∵∠DEA=90°,
∴△CHD≌△DEA,
∴AE=HD=1,CH=DE=m+1,
∴EH=HD+DE=1+m+1=m+2,
由OC=EH得m2+2m=m+2,解得m1=1,m2=﹣2(舍去),
∴抛物线C2的解析式为:y=(x﹣2)2﹣1.
(3)如图2,连接BC,BP,
由抛物线对称性可知AP=BP,
∵△PAC为等边三角形,
∴AP=BP=CP,∠APC=60°,
∴C,A,B三点在以点P为圆心,PA为半径的圆上,
∴∠CBO=∠CPA=30°,
∴BC=2OC,
∴由勾股定理得OB==OC,
∴(m2+2m)=m+2,
解得m1=,m2=﹣2(舍去),
∴m=.
点睛:本题主要考查了二次函数综合题,解题的关键是正确作出辅助线,善于利用几何图形有关性质、定理和二次函数的知识求解.
2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟(AB卷)含解析: 这是一份2022-2023学年北京市海淀区七年级上册数学期中专项提升模拟(AB卷)含解析,共41页。试卷主要包含了选一选,填 空 题,解 答 题,附加题等内容,欢迎下载使用。
2022-2023学年北京市海淀区七年级上册数学期末专项提升模拟卷(AB卷)含解析: 这是一份2022-2023学年北京市海淀区七年级上册数学期末专项提升模拟卷(AB卷)含解析,共33页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年北京市海淀区八年级上册数学期末专项提升模拟卷(AB卷)含解析: 这是一份2022-2023学年北京市海淀区八年级上册数学期末专项提升模拟卷(AB卷)含解析,共45页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。












