

2022-2023学年云南省曲靖市中考数学专项突破仿真模拟试题(一模二模)含解析
展开2022-2023学年云南省曲靖市中考数学专项突破仿真模拟试题
(一模)
一、选一选(本题共16个小题,共42分)
1. ﹣2的相反数是( )
A. 2 B. C. ﹣2 D. 以上都没有对
2. 已知mn<0且1﹣m>1﹣n>0>n+m+1,那么n,m,,的大小关系是( )
A. m<<
A. B. C. D.
4. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
A. B. C. D.
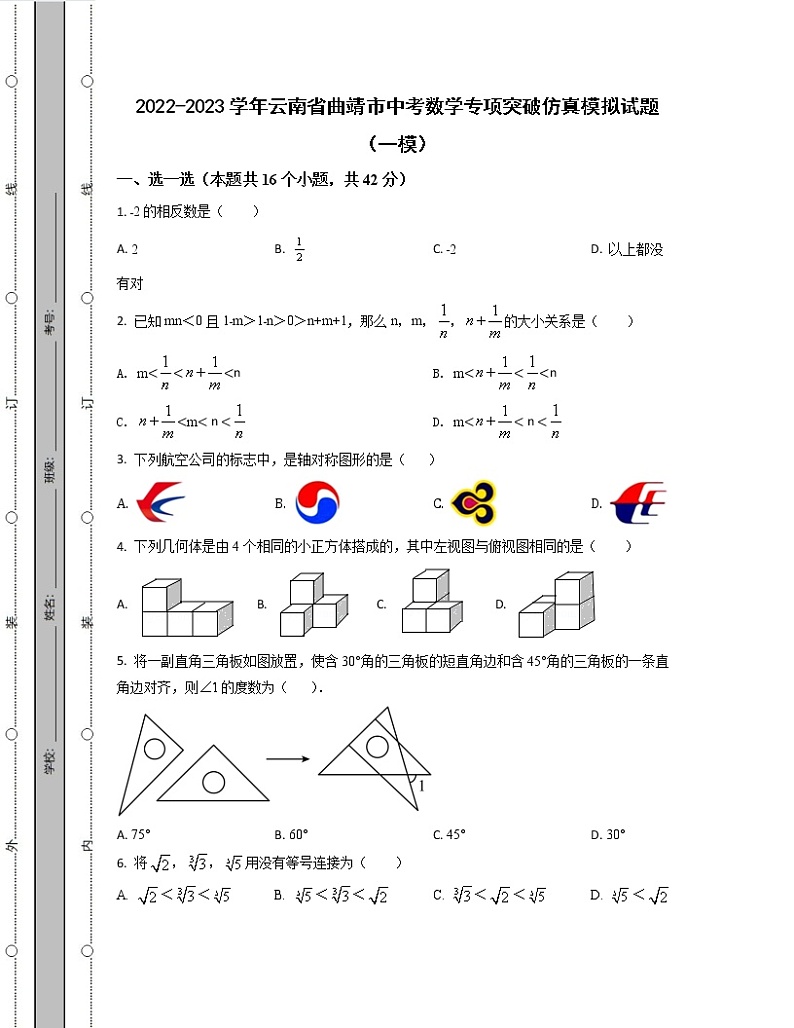
5. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边对齐,则的度数为( ).
A. 75° B. 60° C. 45° D. 30°
6. 将,,用没有等号连接为( )
A. << B. << C. << D. <<
7. 为了解九(1)班学生体温情况,对这个班所有学生测量了体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃)
36.1
36.2
36.3
36.4
36.5
36.6
人数(人)
4
8
8
10
x
2
A. 这些体温的众数是8 B. 这些体温的中位数是36.35
C. 这个班有40名学生 D. x=8
8. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A. 4 B. 6 C. 8 D. 12
9. 如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若∠A=30°,则∠1+∠2=( )
A. 50° B. 60° C. 45° D. 以上都没有对
10. 有下列命题:
(1)有一个角是60°的三角形是等边三角形;
(2)两个无理数的和没有一定是无理数;
(3)各有一个角是100°,腰长为8cm的两个等腰三角形全等;
(4)没有论m为何值,关于x的方程x2+mx﹣m﹣1=0必定有实数根.其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
11. 如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
A. π +1 B. π+2 C. π-1 D. π-2
12. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟h到达B地;
(4)乙车行驶小时或小时,两车恰好相距50km.
正确的个数是( )
A. 1 B. 2 C. 3 D. 4
13. 如图,正方形ABCD的顶点A(0,),B(,0),顶点C,D位于象限,直线x=t,(0≤t≤),将正方形ABCD分成两部分,设位于直线l左侧部分(阴影部分)的面积为S,则函数S与t的图象大致是( )
A. B. C. D.
14. 如图,A、B分别为反比例函数y=﹣(x<0),y=(x>0)图象上的点,且OA⊥OB,则sin∠ABO的值为( )
A. B. C. D.
15. 如图,在矩形中,,,以为斜边在矩形外部作直角三角形,为的中点,则的值为( )
A. B. C. D.
16. 函数y=x2-x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-1时,函数值( )
A. y<0 B. 0<y<m C. y=m D. y>m
二、填 空 题
17. 若一个负数的立方根就是它本身,则这个负数是_____.
18. 如图,在路灯的同侧有两根高度相同的木棒,请分别画出这两根木棒的影子.
19. 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为_____.
三、解 答 题.
20. 先化简再求值:其中x是没有等式组的整数解.
21. 在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,没有放回,再从剩下的卡片中随机抽取一张.
(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
22. 如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,,,是三个格点(即小正方形顶点),判断与的位置关系,并说明理由;
(2)如图②,连接三格和两格的对角线,求的度数(要求:画出示意图,并写出证明过程).
23. 如图,Rt△ABE中,AB⊥AE以AB直径作⊙O,交BE于C,弦CD⊥AB,F为AE上一点,连FC,则FC=FE.
(1)求证CF是⊙O的切线;
(2)已知点P为⊙O上一点,且tan∠APD=,连CP,求sin∠CPD的值.
24. 如图1,△ACB、△AED都为等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连CE,M、N分别为BD、CE的中点.
(1)求证:MN⊥CE;
(2)如图2将△AED绕A点逆时针旋转30°,求证:CE=2MN.
25. 如图,海中有一小岛P,在距小岛P海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能通过这一海域?
26. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个没有同的公共点,试求t的取值范围.
2022-2023学年云南省曲靖市中考数学专项突破仿真模拟试题
(一模)
一、选一选(本题共16个小题,共42分)
1. ﹣2的相反数是( )
A. 2 B. C. ﹣2 D. 以上都没有对
【正确答案】A
【详解】﹣2的相反数是2,
故选:A.
2. 已知mn<0且1﹣m>1﹣n>0>n+m+1,那么n,m,,的大小关系是( )
A. m<<
【详解】∵mn<0,
∴m,n异号,
由1﹣m>1﹣n>0>n+m+1,
可知m<n,m+n>﹣1,m<0,0<n<1,|m|>|n|.
假设符合条件的m=﹣4,n=0.2
则=5,n+=0.2﹣=﹣
则﹣4<﹣<0.2<5
故m<n+<n<.
故选D.
3. 下列航空公司的标志中,是轴对称图形的是( )
A. B. C. D.
【正确答案】C
【分析】根据轴对称图形的概念判断即可.
【详解】解:、没有是轴对称图形,没有合题意;
、没有是轴对称图形,没有合题意;
、是轴对称图形,符合题意;
、没有是轴对称图形,没有合题意;
故选:.
本题考查的是轴对称图形的概念,判断轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
4. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
A. B. C. D.
【正确答案】C
【详解】从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状;
从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状;
从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状.
选项C左视图与俯视图都如下图所示:
故选:C.
5. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边对齐,则的度数为( ).
A. 75° B. 60° C. 45° D. 30°
【正确答案】A
【分析】根据三角板可得:∠2=60°,∠5=45°,然后根据三角形内角和定理可得∠2的度数,进而得到∠4的度数,再根据三角形内角与外角的关系可得∠2的度数.
【详解】解:如图:
由题意得:∠2=60°,∠5=45°,
∵∠2=60°,
∴∠3=180°-90°-60°=30°,
∴∠4=30°,
∴∠1=∠4+∠5=30°+45°=75°
故选:A.
本题考查三角形内角和定理,三角形外角的性质,关键是掌握三角形的一个外角等于和它没有相邻的两个内角和.
6. 将,,用没有等号连接为( )
A. << B. << C. << D. <<
【正确答案】D
【详解】∵ ≈1.414,≈1.442, =1.380,1.380<1.414<1.442,
∴<<.
故选D.
7. 为了解九(1)班学生的体温情况,对这个班所有学生测量了体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃)
36.1
36.2
36.3
36.4
36.5
36.6
人数(人)
4
8
8
10
x
2
A. 这些体温的众数是8 B. 这些体温的中位数是36.35
C. 这个班有40名学生 D. x=8
【正确答案】A
【详解】解:由扇形统计图可知:体温为36.1℃所占的百分数为×=10%,则九(1)班学生总数为=40,故C正确;则x=40﹣(4+8+8+10+2)=8,故D正确;由表可知这些体温的众数是36.4℃,故A错误;由表可知这些体温的中位数是=36.35(℃),
故B正确.故选A.
考点:①扇形统计图;②众数;③中位数.
8. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A. 4 B. 6 C. 8 D. 12
【正确答案】C
【分析】根据三角形内角和定理求得∠C=∠ABC=30°,再根据圆周角定理及直角三角形的性质即可求得BD的长.
【详解】∵∠BAC=120°,AB=AC=4,
∴∠C=∠ABC=30°
∴∠D=30°
∵BD是直径
∴∠BAD=90°
∴BD=2AB=8.
故选:C.
9. 如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若∠A=30°,则∠1+∠2=( )
A. 50° B. 60° C. 45° D. 以上都没有对
【正确答案】B
【详解】试题解析:∵∠1=180﹣2∠ADE;∠2=180﹣2∠AED.
∴∠1+∠2=360°﹣2(∠ADE+∠AED)
=360°﹣2(180°﹣30°)
=60°.
故选B.
10. 有下列命题:
(1)有一个角是60°的三角形是等边三角形;
(2)两个无理数的和没有一定是无理数;
(3)各有一个角是100°,腰长为8cm的两个等腰三角形全等;
(4)没有论m为何值,关于x方程x2+mx﹣m﹣1=0必定有实数根.其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【正确答案】D
【详解】(1)有一个角是60°的三角形是等边三角形;根据等腰三角形的判定,有一个角是60°,的等腰三角形是等边三角形,故本选项正确;
(2)两个无理数的和没有一定是无理数;∵+(﹣)=0,∴两个无理数的和没有一定是无理数,故本选项正确;
(3)各有一个角是100°,腰长为8cm的两个等腰三角形全等;根据等腰三角形的性质,此三角形一定是顶角是100°,腰长为8cm的两个等腰三角形一定全等,故本选项正确;
(4)没有论m为何值,关于x的方程x2+mx﹣m﹣1=0必定有实数根.∵b2﹣4ac=m2﹣4(﹣m﹣1)=(m+2)2≥0,∴没有论m为何值,关于x的方程x2+mx﹣m﹣1=0必定有实数根,故本选项正确;
其中真命题的个数为4个.
故选D.
11. 如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
A. π +1 B. π+2 C. π-1 D. π-2
【正确答案】D
【详解】连接
∵ABCD是正方形,
∴
∴圆内接正方形的边长为,
∴阴影部分的面积为:
故选D.
12. 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟h到达B地;
(4)乙车行驶小时或小时,两车恰好相距50km.
正确的个数是( )
A. 1 B. 2 C. 3 D. 4
【正确答案】C
【详解】(1)由题意,得m=1.5﹣0.5=1.
120÷(3.5﹣0.5)=40(km/h),则a=40,故(1)正确;
(2)120÷(3.5﹣2)=80km/h(千米/小时),故(2)正确;
(3)设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得
解得:
∴y=40x﹣20,
根据图形得知:甲、乙两车中先到达B地的是乙车,
把y=260代入y=40x﹣20得,x=7,
∵乙车的行驶速度:80km/h,
∴乙车的行驶260km需要260÷80=3.25h,
∴7﹣(2+3.25)=h,
∴甲比乙迟h到达B地,故(3)正确;
(4)当15<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得
解得:
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x=.
当40x﹣20+50=80x﹣160时,
解得:x=.
∴﹣2=,﹣2=.
所以乙车行驶小时或小时,两车恰好相距50km,故(4)错误.
故选C.
13. 如图,正方形ABCD的顶点A(0,),B(,0),顶点C,D位于象限,直线x=t,(0≤t≤),将正方形ABCD分成两部分,设位于直线l左侧部分(阴影部分)的面积为S,则函数S与t的图象大致是( )
A. B. C. D.
【正确答案】C
【详解】根据图形知道,当直线x=t在BD的左侧时,如果直线匀速向右运动,左边的图形是三角形;
因而面积应是t的二次函数,并且面积增加的速度随t的增大而增大;
直线x=t在B点左侧时,S=t2,
t在B点右侧时S=﹣(t﹣)2+1,显然D是错误的.
故选C.
14. 如图,A、B分别为反比例函数y=﹣(x<0),y=(x>0)图象上的点,且OA⊥OB,则sin∠ABO的值为( )
A. B. C. D.
【正确答案】C
【详解】过点A作AN⊥x轴于点N,过点B作BM⊥x轴于点M,如图所示:
∵A、B分别为反比例函数y=﹣(x<0),y=(x>0)图象上的点,
∴S△ANO=×2=1,
S△BOM=×8=4,
∴=,
∵∠AOB=90°,
∴∠AON+∠BOM=90°,
∵∠BOM+∠OBM=90°,
∴∠AON=∠OBM,
又∵∠ANO=∠OMB,
∴△AON∽△OBM,
∴,
∴设AO=x,则BO=2x,故AB= x,
故sin∠ABO=.
故选C.
15. 如图,在矩形中,,,以为斜边在矩形外部作直角三角形,为的中点,则的值为( )
A. B. C. D.
【正确答案】C
【详解】由题意知∠BEC=90°,
∴点E在以BC为直径的⊙O上,如图所示:
由图可知,连接FO并延长交⊙O于点E′,
此时E′F最长,
∵CO=BC=6、FC=CD=,
∴OF==,
则E′F=OE′+OF=6+=,
故选C.
考查圆周角定理及勾股定理,根据圆周角定理得出点E在以BC为直径的⊙O上,从而确定出使EF最长的点E的位置是解题的关键.
16. 函数y=x2-x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-1时,函数值( )
A. y<0 B. 0<y<m C. y=m D. y>m
【正确答案】D
【分析】根据对称轴及函数值判断a的取值范围,从而得出a-1<0,因为当x<时,
y随x的增大而减小,所以当x=a-1<0时,函数值y一定大于m.
【详解】解:∵函数y=x2-x+m(m为常数)对称轴是x=,0<<
∴由对称性得:<<1
∵当x=a时,y<0,
∴a的范围是
∵当x<时y随x的增大而减小,
当x=0时函数值是m.
∴当x=a−1<0时,函数值y一定大于m.
故选:D.
本题考查二次函数的性质,解题的关键是根据对称轴及二次函数的性质求解.
二、填 空 题
17. 若一个负数的立方根就是它本身,则这个负数是_____.
【正确答案】-1
【详解】解:根据题意得:﹣1的立方根是它本身,即这个负数是﹣1,
故答案为﹣1.
18. 如图,在路灯的同侧有两根高度相同的木棒,请分别画出这两根木棒的影子.
【正确答案】见解析
【详解】试题分析:根据光源和两根木棒的物高得影子长即可
试题解析:
如图所示:
考查投影的特点与应用,解决本题的关键是根据光源和两根木棒的物高得影子长.
19. 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为_____.
【正确答案】31008.
【详解】∵∠A1A2O=30°,点A1的坐标为(1,0),
∴点A2的坐标为(0,).
∵A2A3⊥A1A2,
∴点A3的坐标为(﹣3,0).
同理可得:A4(0,﹣3),A5(9,0),A6(0,9),…,
∴A4n+1(,0),A4n+2(0,),A4n+3(﹣,0),A4n+4(0,﹣)(n为自然数).
∵2017=504×4+1,
∴A2017(,0),即(31008,0).
故答案为31008.
本题考查了规律型中点坐标以及含30度角的直角三角形,根据点的变化找出变化规律,是解题的关键.
三、解 答 题.
20. 先化简再求值:其中x是没有等式组的整数解.
【正确答案】-1
【详解】试题分析:根据分式的减法和除法可以化简题目中的式子,然后根据x是没有等式组的整数解,从而可以的相应的x的值,注意取得的x的值必须使得原分式有意义.
试题解析:
=
=
=,
由没有等式,得到﹣1<x<1,
由x为整数,得到x=0,
则原式=﹣1.
21. 在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,没有放回,再从剩下的卡片中随机抽取一张.
(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
【正确答案】(1)图形见解析(2)
【分析】(1)本题属于没有放回的情况,画出树状图时要注意;
(2)B、C、D三个卡片的上的数字是勾股数,选出选中B、C、D其中两个的即可
【详解】(1)画树状图如下:
(2)∵共有12种等可能的结果数,抽到的两张卡片上的数都是勾股数的结果数为6种,
∴抽到的两张卡片上的数都是勾股数的概率.
22. 如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,,,是三个格点(即小正方形的顶点),判断与的位置关系,并说明理由;
(2)如图②,连接三格和两格的对角线,求的度数(要求:画出示意图,并写出证明过程).
【正确答案】(1),理由见解析;(2),理由见解析.
【分析】(1)连接AC,再利用勾股定理列式求出AB2、BC2、AC2,然后利用勾股定理逆定理解答;
(2)根据勾股定理的逆定理判定△ABC是等腰直角三角形,根据全等三角形的判定和性质,可得结果.
【详解】解:(1),
理由:如图①,连接,
由勾股定理可得,,,
所以,
所以是直角三角形且,
所以,
(2).
理由:如图②,连接AB 、BC,
由勾股定理得,
,
,
所以,
所以是直角三角形且.
又因为,所以是等腰直角三角形,
∴∠CAB=45°,
在△ABE和△FCD中,
,
∴△ABE≌△FCD(SAS),
∴∠BAD=∠β,
∴∠α+∠β=∠CAD+∠BAD=45°.
本题考查了勾股定理、勾股定理逆定理、等腰直角三角形的判定与性质,以及全等三角形的判定与性质,熟练掌握网格结构以及勾股定理和逆定理是解题的关键.
23. 如图,Rt△ABE中,AB⊥AE以AB为直径作⊙O,交BE于C,弦CD⊥AB,F为AE上一点,连FC,则FC=FE.
(1)求证CF是⊙O的切线;
(2)已知点P为⊙O上一点,且tan∠APD=,连CP,求sin∠CPD的值.
【正确答案】(1)证明见解析;(2)
【详解】试题分析:
试题解析:
(1)证明:连接OC,
∵AB是直径,
∴∠BAE=90°,
∴∠B+∠E=90°,
又∵OB=OC,CF=EF,
∴∠BCO=∠CBO,∠E=∠ECF,
∴∠BCO+∠ECF=90°,
∴∠FCO=90°,
∴CF是⊙O切线;
(2)解:∵CD⊥AB,
∴ ,
∴∠B=∠APD,∠COM=∠CPD,
∴tan∠APD=tan∠B=,
设CM=t,BM=2t,OB=OC=R,OM=2t﹣R,
∴R2=t2+(2t﹣R)2,
∴R=,
∴sin∠CPD=sin∠COM=.
24. 如图1,△ACB、△AED都为等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连CE,M、N分别为BD、CE的中点.
(1)求证:MN⊥CE;
(2)如图2将△AED绕A点逆时针旋转30°,求证:CE=2MN.
【正确答案】(1)证明见解析;(2)证明见解析.
【详解】试题分析:(1)延长DN交AC于F,连BF,推出DE∥AC,推出△EDN∽△CFN,推出,求出DN=FN,FC=ED,得出MN是中位线,推出MN∥BF,证△CAE≌△BCF,推出∠ACE=∠CBF,求出∠CBF+∠BCE=90°,即可得出答案;
(2)延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,求出BG=2MN,证△CAE≌△BCG,推出BG=CE,即可得出答案.
试题解析:
(1)证明:延长DN交AC于F,连BF,
∵N为CE中点,
∴EN=CN,
∵△ACB和△AED是等腰直角三角形,∠AED=∠ACB=90°,DE=AE,AC=BC,
∴∠EAD=∠EDA=∠BAC=45°,
∴DE∥AC,
∴△EDN∽△CFN,
∴ ,
∵EN=NC,
∴DN=FN,FC=ED,
∴MN是△BDF的中位线,
∴MN∥BF,
∵AE=DE,DE=CF,
∴AE=CF,
∵∠EAD=∠BAC=45°,
∴∠EAC=∠ACB=90°,
在△CAE和△BCF中,
,
∴△CAE≌△BCF(SAS),
∴∠ACE=∠CBF,
∵∠ACE+∠BCE=90°,
∴∠CBF+∠BCE=90°,
即BF⊥CE,
∵MN∥BF,
∴MN⊥CE.
(2)证明:延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,
∵M为BD中点,
∴MN是△BDG的中位线,
∴BG=2MN,
在△EDN和⊈CGN中,
,
∴△EDN≌△CGN(SAS),
∴DE=CG=AE,∠GCN=∠DEN,
∴DE∥CG,
∴∠KCG=∠CKE,
∵∠CAE=45°+30°+45°=120°,
∴∠EAK=60°,
∴∠CKE=∠KCG=30°,
∴∠BCG=120°,
在△CAE和△BCG中,
,
∴△CAE≌△BCG(SAS),
∴BG=CE,
∵BG=2MN,
∴CE=2MN.
考查了等腰直角三角形性质,全等三角形的性质和判定,三角形的中位线,平行线性质和判定的应用,主要考查学生的推理能力.
25. 如图,海中有一小岛P,在距小岛P的海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能通过这一海域?
【正确答案】轮船自A处开始至少沿南偏东75°度方向航行,才能通过这一海域.
【详解】试题分析: 过P作PB⊥AM于B,则PC的长是A沿AM方向距离P点的最短距离,求出PC长和16比较即可,第二问设出航行方向,利用角的三角函数值确定答案.
试题解析:过P作PB⊥AM于B,
在Rt△APB中,∵∠PAB=30°,
∴PB=AP=×32=16海里,
∵16<16故轮船有触礁危险
为了,应该变航行方向,并且保证点P到航线的距离没有小于暗礁的半径16海里,即这个距离至少为16海里,
设航向为AC,作PD⊥AC于点D,
由题意得,AP=32海里,PD=16海里,
∵sin∠PAC=,
∴在Rt△PAD中,∠PAC=45°,
∴∠BAC=∠PAC-∠PAB=45°-30°=15°,
答:轮船自A处开始至少沿东偏南15°度方向航行,才能通过这一海域.
26. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个没有同的公共点,试求t的取值范围.
【正确答案】(1)b=﹣2a,顶点D的坐标为(﹣,﹣);(2);(3) 2≤t<.
【分析】(1)把M点坐标代入抛物线解析式可得到b与a的关系,可用a表示出抛物线解析式,化为顶点式可求得其顶点D的坐标;
(2)把点M(1,0)代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得△DMN的面积即可;
(3)先根据a的值确定抛物线的解析式,画出图2,先联立方程组可求得当GH与抛物线只有一个公共点时,t的值,再确定当线段一个端点在抛物线上时,t的值,可得:线段GH与抛物线有两个没有同的公共点时t的取值范围.
【详解】解:(1)∵抛物线y=ax2+ax+b有一个公共点M(1,0),
∴a+a+b=0,即b=-2a,
∴y=ax2+ax+b=ax2+ax-2a=a(x+)2-,
∴抛物线顶点D的坐标为(-,-);
(2)∵直线y=2x+m点M(1,0),
∴0=2×1+m,解得m=-2,
∴y=2x-2,
则,
得ax2+(a-2)x-2a+2=0,
∴(x-1)(ax+2a-2)=0,
解得x=1或x=-2,
∴N点坐标为(-2,-6),
∵a<b,即a<-2a,
∴a<0,
如图1,设抛物线对称轴交直线于点E,
∵抛物线对称轴为,
∴E(-,-3),
∵M(1,0),N(-2,-6),
设△DMN的面积为S,
∴S=S△DEN+S△DEM=|( -2)-1|•|--(-3)|=−−a,
(3)当a=-1时,
抛物线的解析式为:y=-x2-x+2=-(x+)2+,
由,
-x2-x+2=-2x,
解得:x1=2,x2=-1,
∴G(-1,2),
∵点G、H关于原点对称,
∴H(1,-2),
设直线GH平移后的解析式为:y=-2x+t,
-x2-x+2=-2x+t,
x2-x-2+t=0,
△=1-4(t-2)=0,
t=,
当点H平移后落在抛物线上时,坐标为(1,0),
把(1,0)代入y=-2x+t,
t=2,
∴当线段GH与抛物线有两个没有同的公共点,t的取值范围是2≤t<.
本题为二次函数的综合应用,涉及函数图象的交点、二次函数的性质、根的判别式、三角形的面积等知识.在(1)中由M的坐标得到b与a的关系是解题的关键,在(2)中联立两函数解析式,得到关于x的一元二次方程是解题的关键,在(3)中求得GH与抛物线一个交点和两个交点的分界点是解题的关键,本题考查知识点较多,综合性较强,难度较大.
2022-2023学年云南省曲靖市中考数学专项突破仿真模拟试题
(二模)
一、填 空 题(每小题3分,共18分。请考生用黑色碳素笔将答案写在答题卡相应题号后的横线上)
1. ﹣的相反数是_____.
2. 如图,已知,,则______.
3. 化简=_____.
4. 关于x的一元二次方程x2﹣3x+k=0有两个没有相等的实数根,则k的取值范围是_____.
5. 若n边形的内角和是它的外角和的2倍,则n=_______.
6. 如图,OABC为菱形,点C在x轴上,点A在直线y=x上,点B在y=(k>0)的图象上,若S菱形OABC=,则k的值为_____.
二、选一选(每小题4分,共32分。在每小题给出的四个选项中,只有一项是正确的)
7. 下列四个几何体中,主视图是三角形是( )
A. B. C. D.
8. 《2018年政府工作报告》指出“我国五年来,粮食生产能力达到12000亿斤”,将12000亿斤用科学记数法表示应为( )
A. 1.2×103亿斤 B. 12×103亿斤 C. 1.2×104亿斤 D. 0.12×105亿斤
9. 下列计算正确的是( )
A a2+a2=a4 B. a6÷a2=a4 C. (a2)3=a5 D. (a﹣b)2=a2﹣b2
10. 式子中x的取值范围是( )
A. x≤3 B. x<3 C. x≥﹣3 D. x≥3
11. 如图,已知:在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
A. 70° B. 45° C. 35° D. 30°
12. 关于▱ABCD的叙述,正确的是( )
A. 若AB⊥BC,则▱ABCD是菱形 B. 若AC⊥BD,则▱ABCD是正方形
C. 若AC=BD,则▱ABCD是矩形 D. 若AB=AD,则▱ABCD是正方形
13. 2017年,在创建文明城市的进程中,乌鲁木齐市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树x万棵,可列方程是( )
A. B. C. D.
14. 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置时,若AB=2,AD=4,则阴影部分的面积为( )
A. B. C. D.
三、解 答 题(本大题共9小题,满分70分。必须写出运算步骤、推理过程或文字说明,超出答题区域的作答无效)
15. 计算:(1﹣π)0﹣|﹣|+(﹣1)2018﹣()﹣1.
16. 已知:如图,B,F,C,D在同一条直线上,∠ACB=∠EFD,BF=CD,AC=EF.
求证:∠B=∠D.
17. 如图,在平面直角坐标系中,A(﹣2,3),B(﹣5,1),C(﹣1,0).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;
(2)在图中作出△ABC关于原点O成对称的图形△A2B2C2,并写出A2点的坐标;
(3)在y轴上找一点P,使△PAC的周长最小,请直接写出点P的坐标.
18. 为了方便学生参加体育锻炼,某学校准备购买一批运动鞋供学生体育锻炼借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下没有完整的统计图①和图②,请根据有关信息,解答下列问题:
(1)填空:本次随机抽样的学生为 名,本次获取的样本数据的中位数是 号,众数是 号;
(2)补全条形统计图;
(3)根据样本数据,若学校计划购买800双运动鞋,建议购买34号运动鞋多少双?
19. 在甲、乙两个没有透明布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,把球上的数字记为x,再从乙袋中任意摸出一个小球,把球上的数字记为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法(只选其中一种),写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣2x的图象上的概率.
20. 如图,河的两岸MN与PQ相互平行,点A,B是PQ上的两点,C是MN上的点,某人在点A处测得∠CAQ=30°,再沿AQ方向前进20米到达点B,某人在点A处测得∠CAQ=30°,再沿AQ方向前进20米到达点B,测得∠CBQ=60°,求这条河的宽是多少米?(结果到0.1米,参考数据≈1.414,≈1.732)
21. 某小区为了美化环境,计划分两次购进A,B两种花,次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.
(1)求A、B两种花的单价分别是多少元?
(2)若购买A、B两种花共31棵,且B种花数量没有多于A种花的数量的2倍,请你给出一种费用最省的,并求出该所需费用.
22. 如图,已知Rt△ABC中,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求⊙O的半径.
23. 如图,在平面直角坐标系中,已知抛物线原点O,顶点为A(1,1),且与直线y=x﹣2相交于B,C两点.
(1)求抛物线的解析式;
(2)求B、C两点坐标;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若没有存在,请说明理由.
2022-2023学年云南省曲靖市中考数学专项突破仿真模拟试题
(二模)
一、填 空 题(每小题3分,共18分。请考生用黑色碳素笔将答案写在答题卡相应题号后的横线上)
1. ﹣的相反数是_____.
【正确答案】
【详解】根据相反数的定义可知的相反数是.
故填.
2. 如图,已知,,则______.
【正确答案】
【分析】根据邻补角的定义求出,再根据两直线平行,同位角相等解答即可.
【详解】解:如图,
,
,
∵AB//CD,
.
故
本题考查了平行线的性质,邻补角的定义,是基础题,熟记性质与概念是解题的关键.
3. 化简=_____.
【正确答案】a+1
【分析】根据分式的基本性质,转化为同分母分式,再利用同分母分式的减法法则计算即可得到结果.
【详解】解:原式==
故答案为
点睛:此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.
4. 关于x的一元二次方程x2﹣3x+k=0有两个没有相等的实数根,则k的取值范围是_____.
【正确答案】k<.
【分析】根据一元二次方程x2﹣3x+k=0有两个没有相等实数根,所以∆>0 ,从而列出关于k的没有等式,解没有等式求出k的取值范围.
【详解】解:一元二次方程x2﹣3x+k=0有两个没有相等的实数根,
9-4k>0,
解之得,k<.
故答案为k<.
点睛: 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式∆=b2﹣4ac:当∆>0时,一元二次方程有两个没有相等的实数根;当∆=0时,一元二次方程有两个相等的实数根;当∆<0时,一元二次方程没有实数根.
5. 若n边形的内角和是它的外角和的2倍,则n=_______.
【正确答案】6
【分析】根据多边形内角和公式:(n-2)•180°(n≥3且n为整数),题意可列出方程180°(n-2)=360°×2,再解即可.
【详解】解:多边形内角和=180(n-2), 外角和=360°,
所以,由题意可得180(n-2)=2×360,
解得:n=6.
故6.
此题主要考查了多边形内角和和外角和,关键是掌握多边形内角和公式:(n-2)•180°(n≥3且n为整数),多边形的外角和等于360度.
6. 如图,OABC为菱形,点C在x轴上,点A在直线y=x上,点B在y=(k>0)的图象上,若S菱形OABC=,则k的值为_____.
【正确答案】
【详解】分析:首先根据直线点A,设A(a,a),再利用勾股定理算出进而得到再利用菱形的面积公式计算出a的值,进而得到A点坐标,进而得到B点坐标,再利用待定系数法求出反比例函数表达式.
详解:∵直线y=x点A,
∴设A(a,a),
∴
∴
∵四边形ABCD是菱形,
∴
∵菱形OABC的面积是,
∴ ∴a=1,
∴
∴
设反比例函数解析式为
∵在反比例函数图象上,
∴
故答案为
点睛:考查反比例函数系数k的几何意义, 菱形的性质,熟练掌握菱形的性质是解题的关键.
二、选一选(每小题4分,共32分。在每小题给出的四个选项中,只有一项是正确的)
7. 下列四个几何体中,主视图是三角形的是( )
A. B. C. D.
【正确答案】B
【详解】主视图是三角形的一定是一个锥体,只有B是锥体.
故选B.
8. 《2018年政府工作报告》指出“我国五年来,粮食生产能力达到12000亿斤”,将12000亿斤用科学记数法表示应为( )
A. 1.2×103亿斤 B. 12×103亿斤 C. 1.2×104亿斤 D. 0.12×105亿斤
【正确答案】C
【详解】分析:科学记数法的表示形式为的形式,其中 为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的值与小数点移动的位数相同.当原数值>1时,是正数;当原数的值<1时,是负数.
详解:12000亿斤用科学记数法可以表示为1.2×104亿斤.
故选C.
点睛:考查科学记数法,掌握值大于1的数的表示方法是解题的关键.
9. 下列计算正确的是( )
A. a2+a2=a4 B. a6÷a2=a4 C. (a2)3=a5 D. (a﹣b)2=a2﹣b2
【正确答案】B
【详解】解:A. a2+a2=2a2,故A选项错误;
B. a6÷a2=a4,故B正确;
C. (a2)3=a6,故C选项错误;
D. (a−b)2=a2+b2−2ab,故D选项错误.
故选B.
10. 式子中x的取值范围是( )
A x≤3 B. x<3 C. x≥﹣3 D. x≥3
【正确答案】D
【详解】分析:根据二次根式的被开方数是非负数解答即可.
详解:根据题意,得:
x﹣3≥0,解得:x≥3;
故选D.
点睛:考查了二次根式的意义和性质.概念:式子(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.
11. 如图,已知:在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
A. 70° B. 45° C. 35° D. 30°
【正确答案】C
【分析】先根据垂径定理得出=,再由圆周角定理即可得出结论.
【详解】解:∵OA⊥BC,∠AOB=70°,
∴=,
∴∠ADC=∠AOB=35°.
故选C.
本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.
12. 关于▱ABCD的叙述,正确的是( )
A. 若AB⊥BC,则▱ABCD是菱形 B. 若AC⊥BD,则▱ABCD是正方形
C. 若AC=BD,则▱ABCD是矩形 D. 若AB=AD,则▱ABCD是正方形
【正确答案】C
【详解】解:A、若AB⊥BC,则▱ABCD是矩形,故本选项没有符合题意;
B、若AC⊥BD,则▱ABCD菱形,故本选项没有符合题意;
C、若AC=BD,则▱ABCD是矩形,故本选项符合题意;
D、若AB=AD,则▱ABCD是菱形,故本选项没有符合题意;
故选:C
13. 2017年,在创建文明城市的进程中,乌鲁木齐市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树x万棵,可列方程是( )
A. B. C. D.
【正确答案】A
【详解】分析:设原计划每天植树x万棵,需要天完成,实际每天植树万棵,需要天完成,根据提前5天完成任务列方程即可.
详解:设原计划每天植树x万棵,需要天完成,则实际每天植树万棵,需要天完成,
∵提前5天完成任务,
∴,
故选A.
点睛:本题考查分式方程的应用,解题的关键是利用题目中的等量关系,本题属于基础题型.
14. 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置时,若AB=2,AD=4,则阴影部分的面积为( )
A. B. C. D.
【正确答案】D
【详解】∵四边形ABCD是矩形,
∴AD=BC=4,CD=AB=2,
∴CE=BC=4,
∴CE=2CD,
∴
∴,
由勾股定理得:
∴阴影部分的面积是S=S扇形CEB′−S△CDE
故选D.
三、解 答 题(本大题共9小题,满分70分。必须写出运算步骤、推理过程或文字说明,超出答题区域的作答无效)
15. 计算:(1﹣π)0﹣|﹣|+(﹣1)2018﹣()﹣1.
【正确答案】
【详解】分析:按照实数的运算顺序进行运算即可.
详解:原式
点睛:本题考查实数的运算,主要考查零次幂,负整数指数幂,乘方以及二次根式,熟练掌握各个知识点是解题的关键.
16. 已知:如图,B,F,C,D在同一条直线上,∠ACB=∠EFD,BF=CD,AC=EF.
求证:∠B=∠D.
【正确答案】证明见解析
【详解】分析:先根据BF=CD得出BC=DF,再由SAS定理得出△ABC≌△EDF,由全等三角形的性质得出∠B=∠D,由此可得出结论.
详解:证明:∵BF=CD,
∴BF+FC=CD+FC,即BC=DF.
在△ABC与△EDF中,
∴△ABC≌△EDF(SAS),
∴∠B=∠D.
点睛:考查全等三角形的判定与性质,熟练掌握三角形全等的判定方法是解题的关键.
17. 如图,在平面直角坐标系中,A(﹣2,3),B(﹣5,1),C(﹣1,0).
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1;
(2)在图中作出△ABC关于原点O成对称的图形△A2B2C2,并写出A2点的坐标;
(3)在y轴上找一点P,使△PAC的周长最小,请直接写出点P的坐标.
【正确答案】(1)作图见解析;(2)作图见解析,A2(2,﹣3);(3)P(0,1).
【详解】分析:先作出各点关于轴的对称点,再顺次连接即可;
先作出各点关于原点的对称点,再顺次连接即可;
连接AC2交y轴于点P,利用待定系数法求出直线的解析式,进而可得出P点坐标;
详解:(1)即为所求;
(2)即为所求;
(3)作点C关于y轴的对称点连接AC2交y轴于点P,点P即为所求.
∵直线的解析式为
∴
点睛:考查作图-轴对称变换, 对称变换,轴对称-最短路线问题,比较简单,是中考命题的.
18. 为了方便学生参加体育锻炼,某学校准备购买一批运动鞋供学生体育锻炼借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下没有完整的统计图①和图②,请根据有关信息,解答下列问题:
(1)填空:本次随机抽样的学生为 名,本次获取的样本数据的中位数是 号,众数是 号;
(2)补全条形统计图;
(3)根据样本数据,若学校计划购买800双运动鞋,建议购买34号运动鞋多少双?
【正确答案】(1)40、36、35;(2)作图见解析;(3)购买34号运动鞋约为120双.
【详解】分析:根据35号运动鞋有12双,占的比例为30%,即可求出总人数,找出出现次数至多的即为众数,将数据按照从小到大顺序排列,求出中位数即可;
求出34号运动鞋的人数,补全统计图即可.
根据题意列出算式,计算即可得到结果.
详解:(1)本次的学生人数为12÷30%=40人,
∵在这组样本数据中,35出现了12次,出现次数至多,
∴这组样本数据的众数为35;
∵将这组样本数据从小到大得顺序排列,其中处于中间的两个数都为36,
∴中位数为
故答案为40、36、35;
(2)34号的人数为40﹣(12+10+8+4)=6,
补全图形如下:
(3)34号:﹣30%﹣25%﹣20%﹣10%=15%,
800×15%=120,
答:购买34号运动鞋约120双.
点睛:考查条形统计图, 用样本估计总体, 扇形统计图, 中位数, 众数,比较基础,是中考命题的.
19. 在甲、乙两个没有透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,把球上的数字记为x,再从乙袋中任意摸出一个小球,把球上的数字记为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法(只选其中一种),写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣2x的图象上的概率.
【正确答案】(1)列表见解析,共有9种结果,且每种结果发生的可能性相同;(2)
【分析】列表或者画树状图写出所有的情况,根据概率的求法计算概率.
【详解】解:(1)列表如下:
﹣1
﹣2
0
0
(0,﹣1)
(0,﹣2)
(0,0)
1
(1,﹣1)
(1,﹣2)
(1,0)
2
(2,﹣1)
(2,﹣2)
(2,0)
共有9种结果,且每种结果发生的可能性相同;
(2)∵点在函数的图象上有两种情况,分别为,
∴点在函数的图象上的概率.
考查概率的计算,明确概率的意义是解题的关键,概率等于所求情况数与总情况数的比.
20. 如图,河的两岸MN与PQ相互平行,点A,B是PQ上的两点,C是MN上的点,某人在点A处测得∠CAQ=30°,再沿AQ方向前进20米到达点B,某人在点A处测得∠CAQ=30°,再沿AQ方向前进20米到达点B,测得∠CBQ=60°,求这条河的宽是多少米?(结果到0.1米,参考数据≈1.414,≈1.732)
【正确答案】17.3米.
【详解】分析:过点C作于D,根据,得到 ,在中,解三角形即可得到河的宽度.
详解:过点C作于D,
∵
∴
∴米,
在中,
∵
∴
∴
∴米,
∴米.
答:这条河的宽是米.
点睛:考查解直角三角形的应用,作出辅助线,构造直角三角形是解题的关键.
21. 某小区为了美化环境,计划分两次购进A,B两种花,次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.
(1)求A、B两种花的单价分别是多少元?
(2)若购买A、B两种花共31棵,且B种花的数量没有多于A种花的数量的2倍,请你给出一种费用最省的,并求出该所需费用.
【正确答案】(1)A种花的单价为20元,B种花的单价为5元.(2)购进A种花11棵、B种花20棵时,费用最省,最省费用是320元.
【详解】分析:(1)设A种花草每棵的价格x元,B种花草每棵的价格y元,根据次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.列出方程组,即可解答.
(2)设A种花草的数量为m棵,则B种花草的数量为(31−m)棵,根据B种花草的数量没有多于A种花草的数量的2倍,得出m的范围,设总费用为W元,根据总费用=两种花草的费用之和建立函数关系式,由函数的性质就可以求出结论.
详解:(1)设A种花草每棵的价格x元,B种花草每棵的价格y元,根据题意得:
解得:
∴A种花草每棵的价格是20元,B种花草每棵的价格是5元.
(2)设A种花草的数量为m棵,则B种花草的数量为(31−m)棵,
∵B种花草的数量没有多于A种花草的数量的2倍,
∴
解得:
∵m是正整数,
∴m最小值=11,
设购买树苗总费用为W=20m+5(31−m)=15m+155,
∵k>0,
∴W随x的减小而减小,
当m=11时,W最小值=15×11+155=320(元).
答:购进A种花草的数量为11棵、B种20棵,费用最省;最省费用是320元.
点睛:考查函数应用, 二元方程组的应用,关键是找出题目中的等量关系列出方程组.
22. 如图,已知Rt△ABC中,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求⊙O的半径.
【正确答案】(1)证明见解析;(2)
【详解】试题分析:(1)求出∠OED=∠BCA=90°,根据切线的判定即可得出结论;
(2)求出△BEC∽△BCA,得出比例式,代入求出即可.
试题解析:(1)证明:连接OE、EC.
∵AC是⊙O的直径,∴∠AEC=∠BEC=90°.∵D为BC的中点,∴ED=DC=BD,∴∠1=∠2.∵OE=OC,∴∠3=∠4,∴∠1+∠3=∠2+∠4,即∠OED=∠ACB.
∵∠ACB=90°,∴∠OED=90°,∴DE是⊙O的切线;
(2)由(1)知:∠BEC=90°.在Rt△BEC与Rt△BCA中,∵∠B=∠B,∠BEC=∠BCA,∴△BEC∽△BCA,∴BE:BC=BC:BA,∴BC2=BE•BA.∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x.∵BC=6,∴62=2x•3x,解得:x=,即AE=,∴AB=,∴AC==,∴⊙O的半径=.
点睛:本题考查了切线的判定和相似三角形的性质和判定,能求出∠OED=∠BCA和△BEC∽△BCA是解答此题的关键.
23. 如图,在平面直角坐标系中,已知抛物线原点O,顶点为A(1,1),且与直线y=x﹣2相交于B,C两点.
(1)求抛物线的解析式;
(2)求B、C两点的坐标;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若没有存在,请说明理由.
【正确答案】(1)y=﹣x2+2x;(2)B(2,0),C(﹣1,﹣3);(3)存在,存在满足条件的N点,其坐标为(,0)或(,0)或(﹣1,0)或(5,0).
【详解】(1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C点坐标;
(2)分别过A、C两点作x轴的垂线,交x轴于点D、E两点,A、B、C三点的坐标可求得∠ABO=∠CBO=45°,可证得结论;
(3)设出N点坐标,可表示出M点坐标,从而可表示出MN、ON的长度,当△MON和△ABC相似时,利用三角形相似的性质可得或,可求得N点的坐标.
解:(1)∵顶点坐标为(1,1),
∴设抛物线解析式为y=a(x﹣1)2+1,
又抛物线过原点,
∴0=a(0﹣1)2+1,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+1,
即y=﹣x2+2x,
联立抛物线和直线解析式可得,解得或,
∴B(2,0),C(﹣1,﹣3);
(2)如图,分别过A、C两点作x轴的垂线,交x轴于点D、E两点,
则AD=OD=BD=1,BE=OB+OE=2+1=3,EC=3,
∴∠ABO=∠CBO=45°,即∠ABC=90°,
∴△ABC是直角三角形;
(3)假设存在满足条件的点N,设N(x,0),则M(x,﹣x2+2x),
∴ON=|x|,MN=|﹣x2+2x|,
由(2)在Rt△ABD和Rt△CEB中,可分别求得AB=,BC=3,
∵MN⊥x轴于点N
∴∠ABC=∠MNO=90°,
∴当△ABC和△MNO相似时有或,
①当时,则有=,即|x||﹣x+2|=|x|,
∵当x=0时M、O、N没有能构成三角形,
∴x≠0,
∴|﹣x+2|=,即﹣x+2=±,解得x=或x=,
此时N点坐标为(,0)或(,0);
②当时,则有=,即|x||﹣x+2|=3|x|,
∴|﹣x+2|=3,即﹣x+2=±3,解得x=5或x=﹣1,
此时N点坐标为(﹣1,0)或(5,0),
综上可知存在满足条件的N点,其坐标为(,0)或(,0)或(﹣1,0)或(5,0).
“点睛”本题为二次函数的综合应用,涉及知识点有待定系数法、图象的交点问题、直角三角形的判定、勾股定理、相似三角形的性质及分类讨论等.在(1)中注意顶点式的运用,在(3)中设出N、M的坐标,利用相似三角形的性质得到关于坐标的方程是解题的关键,注意相似三角形点的对应.本题考查知识点较多,综合性较强,难度适中.
2022-2023学年重庆市江津区中考数学专项突破仿真模拟试题(一模二模)含解析: 这是一份2022-2023学年重庆市江津区中考数学专项突破仿真模拟试题(一模二模)含解析,共57页。试卷主要包含了选一选,填 空 题,计算题,解 答 题等内容,欢迎下载使用。
2022-2023学年重庆市区域中考数学专项突破仿真模拟试题(一模二模)含解析: 这是一份2022-2023学年重庆市区域中考数学专项突破仿真模拟试题(一模二模)含解析,共58页。试卷主要包含了 的整数部分是, 估算 的值,它的整数部分是等内容,欢迎下载使用。
2022-2023学年湖北省襄阳市中考数学专项突破仿真模拟试题(一模二模)含解析: 这是一份2022-2023学年湖北省襄阳市中考数学专项突破仿真模拟试题(一模二模)含解析,共58页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。












