初中数学人教版七年级下册5.3.1 平行线的性质教学ppt课件

这是一份初中数学人教版七年级下册5.3.1 平行线的性质教学ppt课件，共28页。PPT课件主要包含了素养目标，∵a∥b已知，几何语言，连接中考，∠CPD，等量代换，∴∠5∠6等内容，欢迎下载使用。

【思考】根据同位角相等可以判定两直线平行，反过来如果两直线平行，同位角之间有什么关系呢？内错角、同旁内角之间又有什么关系呢？
1. 掌握平行线的性质，会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
3. 区分平行线的性质和判定的关系，培养学生逆向思维的能力.
画两条平行线a//b，然后画一条截线c与a、b相交，标出如图所示的角. 度量所形成的8个角的度数，把结果填入下表：
【讨论】∠1~ ∠8中，哪些是同位角？它们的度数之间有什么关系？说出你的猜想：
猜想：两条平行线被第三条直线所截，同位角＿＿＿.
再任意画一条截线d，同样度量各个角的度数，你的猜想还成立吗？
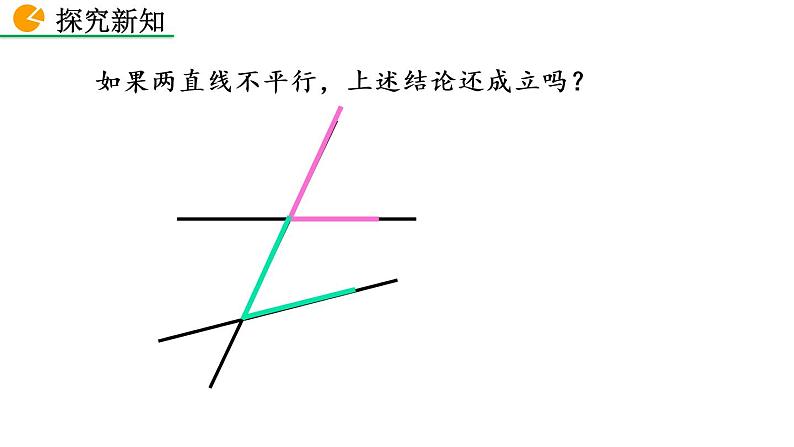
如果两直线不平行，上述结论还成立吗？
一般地，平行线具有如下性质：
性质1：两条平行线被第三条直线所截，同位角相等.
∴∠1=∠2 （两直线平行，同位角相等）.
简单说成：两直线平行，同位角相等.
例 如图，D是AB上一点，E是AC上一点，∠ADE=60°,∠B=60°, ∠AED=40°.（1）DE和BC平行吗？为什么？ （2）∠C是多少度？为什么？
解：（1）DE∥BC， ∵∠ADE＝60°,∠B＝60°，∴∠ADE＝ ∠B. ∴DE∥BC （ ）.
同位角相等，两直线平行
（2） ∠C =40°. ( )∵∠AED=40°，∴∠C =40°.
两直线平行，同位角相等
∵DE∥BC ，∴∠C ＝ ∠AED.
如图所示，∠1＝70°，若m∥n，则∠2＝ .如图所示，直线m∥n，∠1＝70°，∠2＝30°，则∠A等于 ( )A. 30° B. 35° C. 40° D. 50°
在上一节中，我们利用“同位角相等，两直线平行”推出了“内错角相等，两直线平行线”，类似地，已知两直线平行，同位角相等，能否得到内错角之间的数量关系？
如图，已知a//b,那么2与3相等吗？为什么?
解：∵ a∥b(已知), ∴∠1=∠2(两直线平行,同位角相等). 又∵ ∠1=∠3(对顶角相等), ∴ ∠2=∠3(等量代换).
性质2：两条平行线被第三条直线所截，内错角相等.
∴∠2=∠3 （两直线平行，内错角相等）.
简单说成：两直线平行，内错角相等.
例 如图，已知直线a∥b，∠1 = 50°, 求∠2的度数.
∴∠ 2= 50° (等量代换).
解：∵ a∥b(已知),
∴∠ 1= ∠ 2(两直线平行,内错角相等).
又∵∠ 1 = 50° (已知),
利用“两直线平行，内错角相等”求角的度数
如图所示，AC∥BD，∠A＝70°，∠C＝50°，则∠1＝ ，∠2＝ ，∠3＝ .
如图,已知a//b,那么2与4有什么关系呢？为什么?
解: ∵a//b （已知）,
∴ 1=  2（两直线平行，同位角相等）.
∵  1+  4=180°（邻补角的性质）,
∴ 2+  4=180°（等量代换）.
类似地，已知两直线平行，能否得到同旁内角之间的数量关系？
性质3：两条平行线被第三条直线所截，同旁内角互补.
∴∠2+∠4=180 °（两直线平行，同旁内角互补）.
简单说成：两直线平行，同旁内角互补.
例 如图是一块梯形铁片的残余部分，量得∠A=100°，∠B=115°，梯形的另外两个角的度数分别是多少？
解：∵梯形上、下底互相平行， ∴ ∠A与∠D互补， ∠B与∠C互补.
∴梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°∠C= 180 °-∠B=180°-115°=65°
如图所示，直线a∥b，直线l与a，b分别相交于A、B两点，过点A作直线l的垂线交直线b于点C，若∠1＝58°，则∠2的度数为( ) A. 58° B. 42° C. 32° D. 28°
如图，将一块三角尺的直角顶点放在直尺的一边上，当∠1＝35°时，∠2的度数为（　　）A．35° B．45°C．55° D．65°
　　 1.如图所示，直线a∥b，直线c与直线a，b相交，若∠1＝56°，则∠2等于 ( )A. 24° B. 34° C. 56° D. 124°
2.如图所示，AB∥CD，直线EF与AB，CD分别交于点M，N，过点N的直线GH与AB交于点P，则下列结论错误的是( )A. ∠EMB＝∠END B. ∠BMN＝∠MNC C. ∠CNH＝∠BPG D. ∠DNG＝∠AME
3. 如图所示，直线a∥b，点B在直线a上，AB⊥BC，若∠1＝38°，则∠2的度数为 ( )A. 38° B. 52° C. 76° D. 142°
4.如图所示，AB∥CD，∠E＝40°，∠A＝110°，则∠C的度数为( )A. 60° B. 80° C. 75° D. 70°
5. 如图所示，直线a∥b，Rt△ABC的直角顶点C在直线b上，∠1＝20°，则∠2＝ °.
解: ∵ AB∥DE( ),∴∠A= ______ ( ).∵AC∥DF( ), ∴∠D+ _______=180 ( ).∴∠A+∠D=180（ ）.
有这样一道题：如图,若AB∥DE ,　AC∥DF，试说明∠A+∠D=180.请补全下面的解答过程,括号内填写依据.
两直线平行,同位角相等
两直线平行,同旁内角互补
如图，潜望镜中的两面镜子是互相平行放置的，光线经过镜子反射时，∠1=∠2，∠3=∠4，∠2和∠3有什么关系？为什么进入潜望镜的光线和离开潜望镜的光线是平行的？
解：∠2=∠3. ∵两直线平行，内错角相等,
∴∠2=∠3. ∴∠1=∠2=∠3=∠4.∴进入潜望镜的光线和离开潜望镜的光线平行.
∵∠1=∠2，∠3=∠4，