






所属成套资源:北师大版数学八年级下册全册课件PPT+教案+练习(含答案)
初中数学北师大版八年级下册1 等腰三角形获奖课件ppt
展开
这是一份初中数学北师大版八年级下册1 等腰三角形获奖课件ppt,文件包含11等腰三角形第2课时ppt、北师大版数学八年级下册第一章三角形的证明11等腰三角形第2课时教学详案docx、11等腰三角形第二课时同步练习docx等3份课件配套教学资源,其中PPT共14页, 欢迎下载使用。
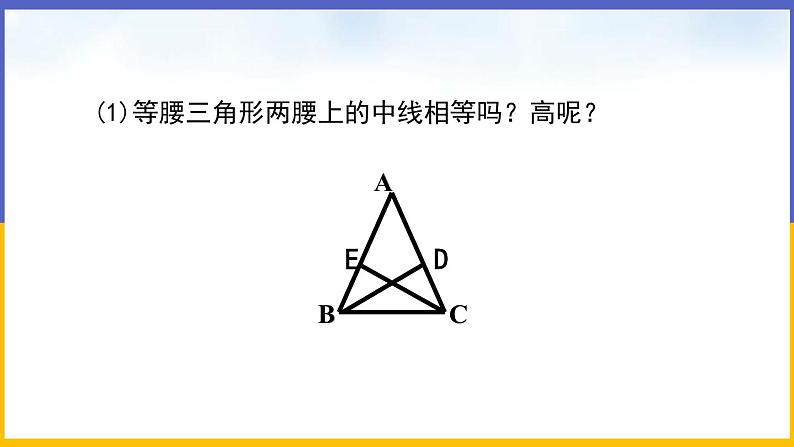
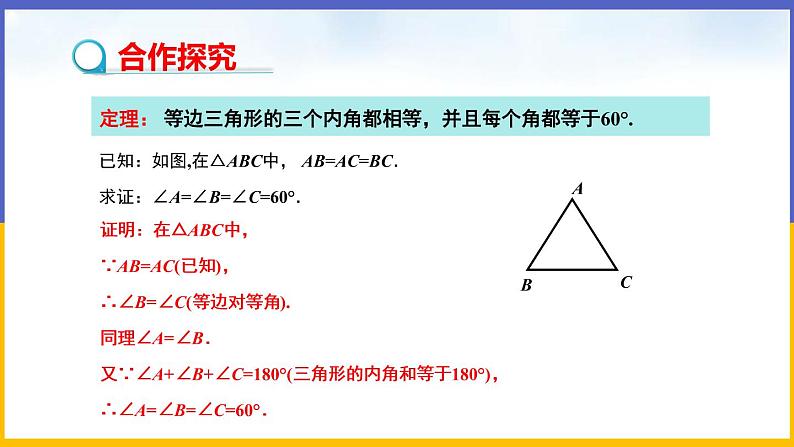
1.1 等腰三角形(第2课时 等边三角形的性质)教学目标1.进一步学习等腰三角形的相关性质,理解等腰三角形两底角的平分线(两腰上的高、中线)的性质.2.学习等边三角形的性质,并能够运用其解决问题.3.把等腰三角形与等边三角形的性质进行比较,体会等腰三角形和等边三角形的相同之处与不同之处.教学重点难点重点:等腰三角形、等边三角形的相关性质.难点:等腰三角形、等边三角形的相关性质的应用.教学过程导入新课在七年级下册我们已经知道了“三边相等的三角形是等边三角形”,生活中有很多等边三角形,如一些交通图标、台球室的三角架等,它们都是等边三角形. 通过上一节课的学习我们知道:等腰三角形的两底角相等以及等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合,那么等腰三角形底角的平分线、两腰上的高具有怎样的性质呢?等边三角形各角之间有什么关系呢?这就是本节课要学习的知识.探究新知一、预习新知(阅读教材P5~P6的内容,回答下面问题)1.等腰三角形两个底角的平分线相等;等腰三角形两腰上的高线相等;等腰三角形两腰上的中线相等.2.等边三角形的三个内角都相等,并且每个角都等于60.二、合作探究问题1 证明:等腰三角形两底角的平分线相等.已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的角平分线.求证:BD=CE.【互动】要证BD=CE,可通过证明三角形全等来解决.证明:∵ AB=AC,∴ ∠ABC=∠ACB(等边对等角),∵ BD,CE分别平分∠ABC和∠ACB,∴ ∠1=∠ABC,∠2=∠ACB.∴ ∠1=∠2.在△BDC和△CEB中,∵ ∠ACB=∠ABC,BC=CB,∠1=∠2,∴ △BDC≌△CEB(ASA).∴ BD=CE(全等三角形的对应边相等).【互动】 等腰三角形两腰上的高呢?中线呢?它们是否也具有这样的关系?【探究】 如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:CD=BE.证明:∵AB=AC,∴∠ABC=∠ACB.又∵CD⊥AB于点D,BE⊥AC于点E,∴∠CEB=∠BDC=90,∴∠EBC=∠DCB.在△BEC和△CDB中, ∴△BEC≌△CDB,∴CD=BE.同样,我们可通过证三角形全等来证明两腰上的中线相等.【总结】(学生总结,老师点评)等腰三角形两底角的平分线相等,两腰上的中线相等,两腰上的高相等. 问题2 证明:等边三角形的三个内角都相等,并且每个角都等于60.已知:如图,在△ABC中, AB=AC=BC.求证:∠A=∠B=∠C=60. 证明:在△ABC中,∵AB=AC(已知),∴∠B=∠C(等边对等角).同理∠A=∠B.又∵∠A+∠B+∠C=180(三角形的内角和等于180),∴∠A=∠B=∠C=60.三、新知应用例 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连结BE,DE.若∠ABE=40,BE=DE,求∠CED的度数.
【探索】(引发学生思考)由△ABC是等边三角形可以得到哪些结论?如何利用这些结论求∠CED的度数?【解】∵△ABC是等边三角形,∴∠ABC=∠ACB=60.∵∠ABE=40,∴∠EBC=∠ABC-∠ABE=20.∵BE=DE,∴∠D=∠EBC=20,∴∠CED=∠ACB-∠D=40.【总结】(学生总结,老师点评)等边三角形是特殊的三角形,它的三个内角都是60,这个性质常常应用在求三角形角的度数的问题上,所以必须熟练掌握.课堂小结(学生总结,老师点评)1.等腰三角形两底角的平分线相等,等腰三角形两腰上的高相等,等腰三角形两腰上的中线相等.2.等边三角形的三个内角都相等,并且每个角都等于60.布置作业请完成教材习题1.2板书设计1 等腰三角形第2课时 等边三角形的性质问题1 证明:等腰三角形两底角的平分线相等等腰三角形两底角的平分线相等,两腰上的中线相等,两腰上的高相等.问题2 证明:等边三角形的三个内角都相等,并且每个角都等于60.例 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连结BE,DE.若∠ABE=40,BE=DE,求∠CED的度数.
相关课件
这是一份初中数学北师大版七年级上册第一章 丰富的图形世界1.1 生活中的立体图形优质课件ppt,文件包含1生活中的立体图形第2课时pptx、2生活中的立体图形第2课时doc等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
这是一份初中数学北师大版八年级下册1 等腰三角形优秀课件ppt,文件包含11等腰三角形第4课时pptx、北师大版数学八年级下册第一章三角形的证明11等腰三角形第4课时教学详案docx、11等腰三角形第四课时同步练习docx等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
这是一份北师大版八年级下册第一章 三角形的证明1 等腰三角形一等奖ppt课件,文件包含11等腰三角形第3课时ppt、北师大版数学八年级下册第一章三角形的证明11等腰三角形第3课时教学详案docx、11等腰三角形第三课时同步练习docx等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。










