2023届江西省贵溪市实验中学三校生高三上学期第二次月考数学试题含解析

这是一份2023届江西省贵溪市实验中学三校生高三上学期第二次月考数学试题含解析，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
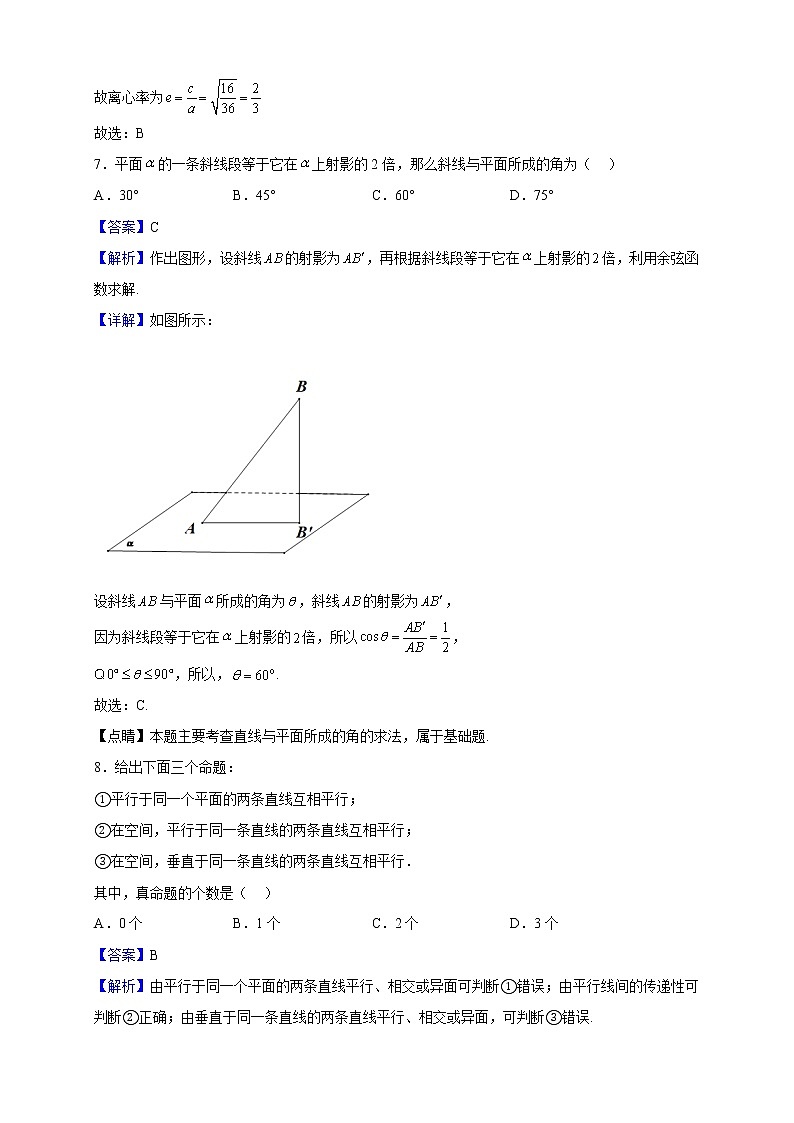
2023届江西省贵溪市实验中学三校生高三上学期第二次月考数学试题 一、单选题1．已知全集，集合，则等于（    ）A． B． C． D．R【答案】B【分析】解不等式确定集合，然后由补集定义求解．【详解】或，所以．故选：B．2．点在直角坐标平面上位于（    ）A．第一象限 B．第二象限C．第三象限 D．第四象限【答案】D【分析】由终边相同角定义确定角所在象限，根据三角函数定义确定符号，然后可得结论．【详解】，是第二象限角，所以，，点在第四象限．故选：D．3．设函数是奇函数，则实数的值等于（    ）A． B．1 C． D．以上都不对【答案】C【分析】利用奇函数的定义，化简解得，然后检验即可.【详解】因为是奇函数，则恒成立，所以有恒成立，化简得，得，要使恒成立，则，解得，当时，，显然不成立，故舍去，当时，，显然可以取.故选：C4．（x）6展开式中常数项是（    ）A．第4项 B．24C C．C D．2【答案】B【分析】在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项．【详解】（x）6展开式的通项公式为，令60，求得，可得展开式中常数项是•24，故选：B【点睛】本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．5．下列直线中与直线垂直的是（   ）A． B． C． D．【答案】B【分析】根据两条直线斜率存在时它们的乘积等于-1逐一判断可得答案.【详解】在直线斜率都存在的情况下，若两直线垂直则斜率乘积为-1，直线的斜率为，选项A：直线的斜率为，显然不与直线垂直，错误；选项B：直线的斜率为5，因为，所以与直线垂直，正确；选项C：直线的斜率为，因为，所以与直线不垂直，错误；选项D：直线的斜率为，显然不与直线垂直，错误，故选：B.6．椭圆的离心率是（    ）A． B． C． D．【答案】B【分析】求出，从而求出离心率.【详解】由题意得：，故，故离心率为故选：B7．平面的一条斜线段等于它在上射影的2倍，那么斜线与平面所成的角为（    ）A．30° B．45° C．60° D．75°【答案】C【解析】作出图形，设斜线的射影为，再根据斜线段等于它在上射影的倍，利用余弦函数求解.【详解】如图所示：设斜线与平面所成的角为，斜线的射影为，因为斜线段等于它在上射影的倍，所以，，所以，.故选：C.【点睛】本题主要考查直线与平面所成的角的求法，属于基础题.8．给出下面三个命题： ①平行于同一个平面的两条直线互相平行；②在空间，平行于同一条直线的两条直线互相平行；③在空间，垂直于同一条直线的两条直线互相平行．其中，真命题的个数是（    ）A．0个 B．1个 C．2个 D．3个【答案】B【解析】由平行于同一个平面的两条直线平行、相交或异面可判断①错误；由平行线间的传递性可判断②正确；由垂直于同一条直线的两条直线平行、相交或异面，可判断③错误.【详解】①平行于同一个平面的两条直线平行、相交或异面，故①错误；②根据空间中平行线间的传递性可知在空间，平行于同一条直线的两条直线互相平行，故②正确；③在空间，垂直于同一条直线的两条直线平行、相交或异面，故③错误.故真命题的个数为1个.故选：B.【点睛】本题考查空间中直线与直线的位置关系的判断，属于基础题. 二、填空题9．函数的值域是_______________.【答案】【分析】先求出函数的定义域为，代入即可求出值域【详解】函数的定义域为，化简得：，解得：，所以函数的值域为.故答案为：10．函数的最小正周期为________.【答案】【分析】利用平方差公式及同角三角函数间基本关系和二倍角公式化简，再利用周期公式求解即可【详解】sin4x-cos4x＝（sin2x-cos2x）（sin2x+cos2x）＝﹣cos 2x则周期 故答案为【点睛】本题考查三角函数化简，考查周期公式，是基础题11．已知是第二象限角，，则__________．【答案】．【分析】由同角间的三角函数关系式计算．【详解】因为，所以，所以，是第二象限角，则，所以．故答案为：．12．若数列的通项公式是则的前项和________．【答案】【分析】根据题意可知：数列是以2为首项，以2为公比的等比数列，代入等比数列的前项和公式即可求解.【详解】因为数列的通项公式为，所以数列是以2为首项，以2为公比的等比数列，由等比数列的前项和公式可得：，故答案为：.13．已知椭圆的方程为，焦点在轴上，的取值范围是______.【答案】【解析】由椭圆的焦点在轴上，可得，求解即可.【详解】由椭圆的方程为，焦点在轴上，可得，所以或，故答案为：【点睛】本题考查了椭圆短轴的范围，是椭圆基本量的考查，属于基础题.14．已知向量，，且，则______________.【答案】【分析】根据向量垂直得到方程，求出，进而求出模长.【详解】由题意得：，解得：，所以，.故答案为：5 三、解答题15．解不等式组：.【答案】【分析】根据绝对值不等式和一元二次不等式解法求出解集.【详解】，，∴不等式得解集为16．已知为坐标原点，，，为坐标平面上一点，且，求点的坐标.【答案】.【分析】由向量线性运算的坐标表示计算．【详解】，则，．即点坐标为．故答案为：．17．在锐角中，角的对边分别为，，，且.(1)求角A的大小；(2)若，，求的面积.【答案】(1)(2) 【分析】（1）根据正弦定理求出，由求出，结合，求出；（2）由余弦定理求出，从而利用三角形面积公式求出答案.【详解】（1），由正弦定理得：，因为，所以，所以，即，因为，所以；（2）由（1）知：，又因为，，由余弦定理得：解得：，所以面积为.18．已知数列是等差数列，且：(1)求数列的通项公式；(2)设数列满足，且数列的前项的积等于，求的值.【答案】(1)；(2). 【分析】（1）利用和建立首项和公差的方程组，即可求得首项和公差，即可得到通项公式；（2）根据题意，结合（1）可以得到数列的前项积，建立关于的方程，即可较易求解.【详解】（1）设等差数列的首项为，公差为，，即，解得：，∴.（2）设数列的前n项的积为，则，∴，，∴.19．在正方体中，若为棱的中点，求异面直线与所成角的余弦值【答案】.【解析】根据题意，可分别以直线，，为，，轴，建立空间直角坐标系，并设正方体的棱长为2，从而可得出向量的坐标，进而可求出的值，从而得出异面直线与所成角的余弦值．【详解】以点为原点，分别以直线，，为，，轴，建立如图所示的空间直角坐标系，设正方体的棱长为2，则：， ， ， ，，，异面直线与所成角的余弦值为．故答案为：【点睛】本题考查了通过建立空间直角坐标系，利用向量坐标解决异面直线所成角的问题的方法，向量夹角的余弦公式，向量坐标的数量积运算，考查了计算能力，属于基础题．20．已知到，距离之和为4，设点的轨迹为，直线与轨迹交于，．（Ⅰ）求轨迹的方程（Ⅱ）若，求．【答案】（Ⅰ）；（Ⅱ）.【解析】（Ⅰ）由椭圆的定义可得曲线的轨迹为椭圆，进而可得轨迹方程；（Ⅱ）联立直线与椭圆的方程，结合韦达定理，由弦长公式可得结果.【详解】（Ⅰ）设，由椭圆定义可知，点的轨迹是以，为焦点，长半轴为2的椭圆．，故曲线的方程为．（Ⅱ）设，，联立有，则且，则所以，整理得解得，所以．【点睛】关键点点睛：本题考查求轨迹方程，解题关键是理解定义．考查了直线与圆锥曲线相交所得弦长问题，本题中直线方程代入椭圆方程整理后应用韦达定理求出，，然后由弦长公式，到所要求的等量关系．考查了学生的运算求解能力，逻辑推理能力．属于中档题.