宁夏银川一中2023届高三上学期第三次月考数学（理）试题（原卷版）

这是一份宁夏银川一中2023届高三上学期第三次月考数学（理）试题（原卷版），共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
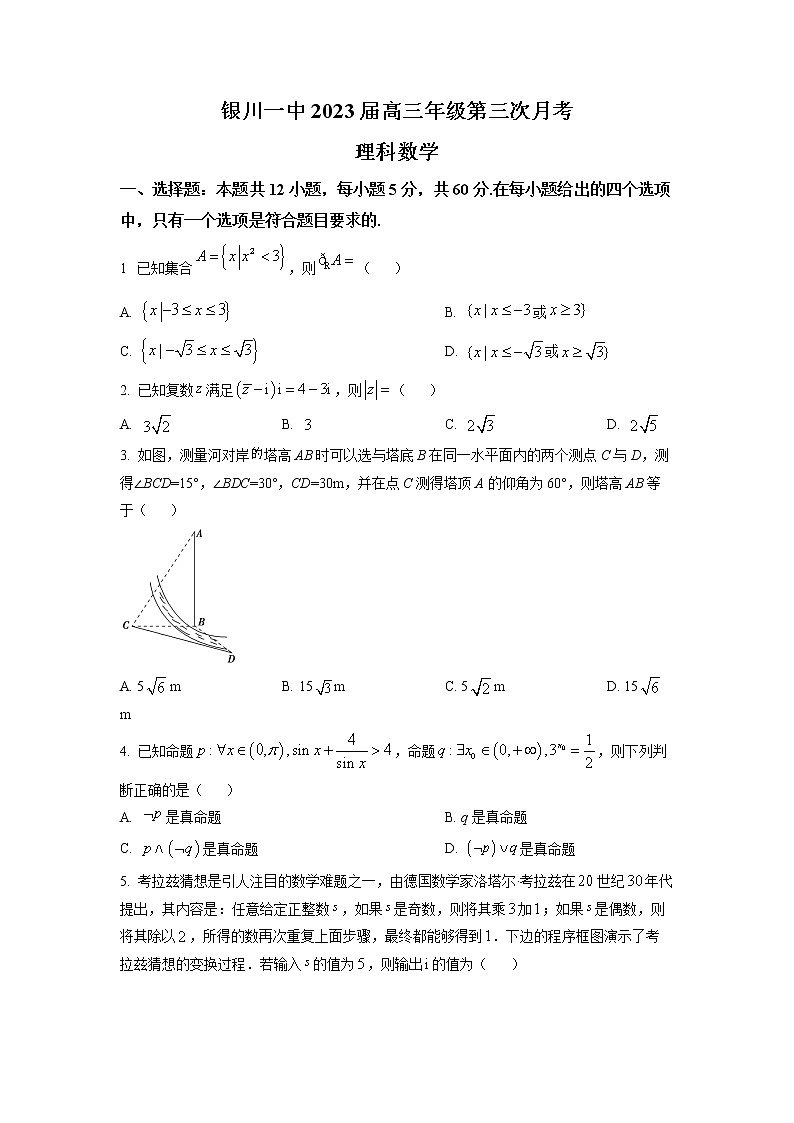
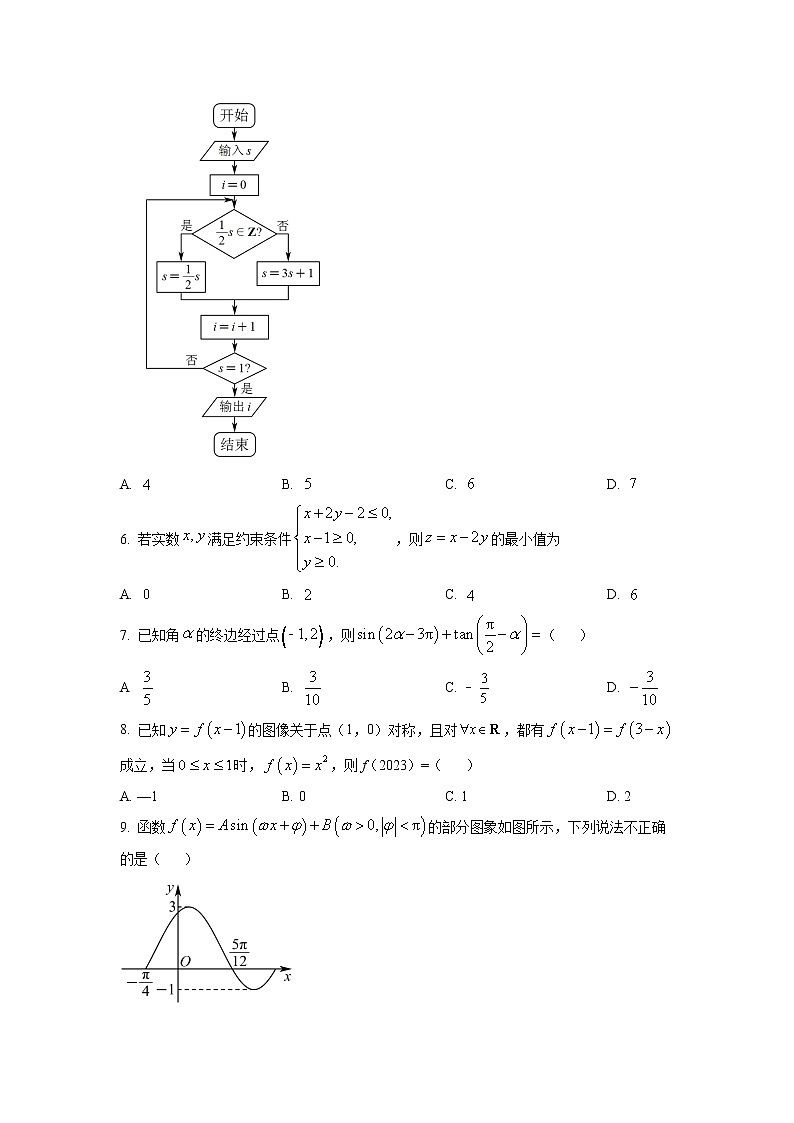
银川一中2023届高三年级第三次月考理科数学一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.1 已知集合，则（    ）A.  B. 或C.  D. 或2. 已知复数满足，则（    ）A.  B.  C.  D. 3. 如图，测量河对岸塔高AB时可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=15°，∠BDC=30°，CD=30m，并在点C测得塔顶A的仰角为60°，则塔高AB等于（    ）A. 5m B. 15m C. 5m D. 15m4. 已知命题，命题，则下列判断正确的是（    ）A. 是真命题 B. q是真命题C. 是真命题 D. 是真命题5. 考拉兹猜想是引人注目的数学难题之一，由德国数学家洛塔尔·考拉兹在世纪年代提出，其内容是：任意给定正整数，如果是奇数，则将其乘加；如果是偶数，则将其除以，所得的数再次重复上面步骤，最终都能够得到．下边的程序框图演示了考拉兹猜想的变换过程．若输入的值为，则输出的值为（    ）A.  B.  C.  D. 6. 若实数满足约束条件，则的最小值为A.  B.  C.  D. 7. 已知角的终边经过点，则（    ）A  B.  C.  D. 8. 已知的图像关于点（1，0）对称，且对，都有成立，当时，，则f（2023）=（    ）A. —1 B. 0 C. 1 D. 29. 函数的部分图象如图所示，下列说法不正确的是（    ）A. 函数的解析式为B. 函数的单调递增区间为C. 为了得到函数的图象，只需将函数的图象向右平移个单位长度，再向上平移一个单位长度D. 函数的图象关于点对称10. 数列满足，，则（    ）A.  B.  C.  D. 11. 若函数与函数有公切线，则实数的取值范围是（    ）A.  B. C.  D. 12. 已知△ABC的内角A，B，C的对边分别为a，b，c，若△ABC是锐角三角形，且满足，若△ABC的面积，则的取值范围是（    ）A.  B. C.  D. 二、填空题：本题共4小题，每小题5分，共20分.13. 定积分__________．14. 已知向量，则在方向上的投影为___________15. 已知函数，，且上单调递减，则_________．16. 已知函数，.若存在，使得关于x的方程有四个不相等的实数解，则n的最大值为_______.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17. 已知函数.（1）求的最小正周期和单调递减区间；（2）若，且，求的值.18. 已知内角A，B，C的对边分别为a，b，c，且.（1）求A；（2）若的外接圆半径为，求面积的最大值.19. 已知函数（1）若函数f（x）在处取得极值，求m；（2）在（1）的条件下，，使得不等式成立，求a的取值范围.20. 设为数列的前项和，已知 ，若数列满足，  （1）求数列和的通项公式；（2）设 求数列的前项的和.21. 已知是自然对数的底数，函数，直线为曲线的切线，.（1）求的值；（2）①判断的零点个数；②定义函数在上单调递增.求实数的取值范围.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.（选修4—4：坐标系与参数方程）22. 在平面直角坐标系中，曲线：（α为参数）经过伸缩变换得到曲线，在以坐标原点为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为. （1）求曲线的普通方程；（2）设点P是曲线上的动点，求点P到直线l距离d的最大值.（选修4—5：不等式选讲）23. 设函数.（1）当时，求不等式的解集；（2）若对，恒成立，求的取值范围.