2023届高考数学二轮复习提升练之三角函数与解三角形——（12）解三角形的实际应用【配套新教材】

（12）解三角形的实际应用【配套新教材】

1.在中，角A，B，C所对的边分别为a，b，c，若，则为(   )

A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形

2.在中，若，则的形状是(   ).

A.直角三角形 B.锐角三角形 C.钝角三角形 D.不确定

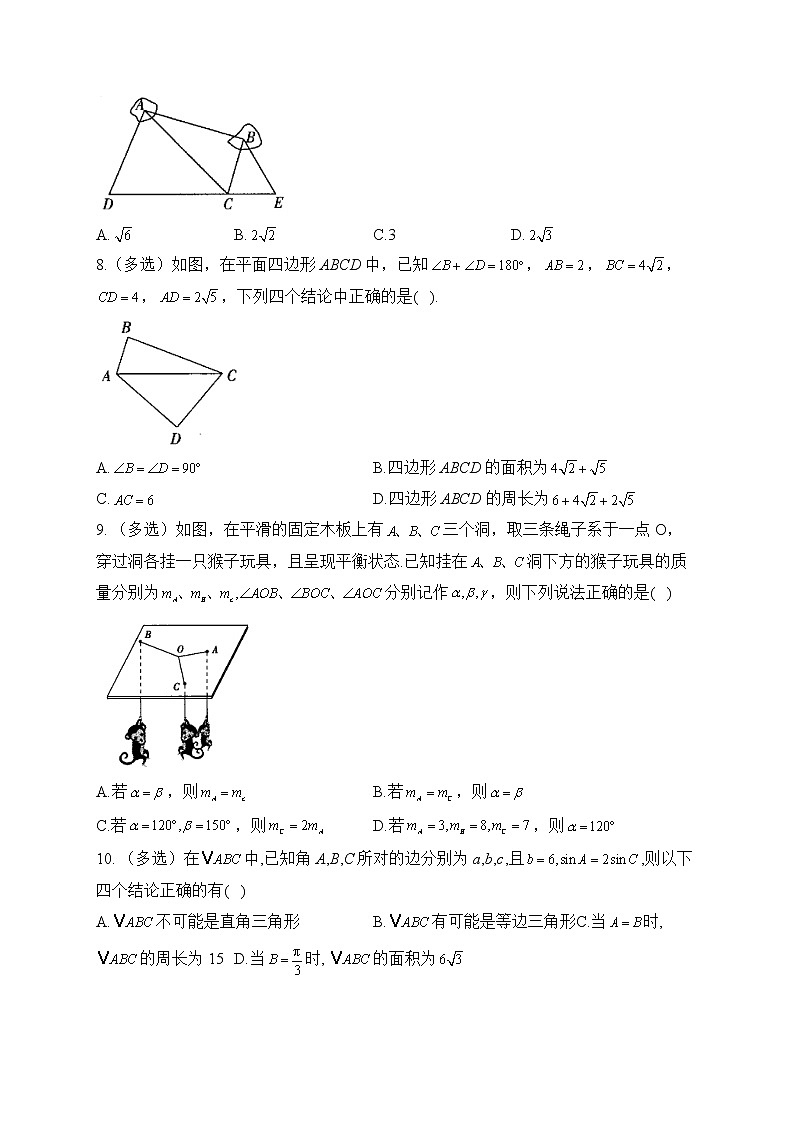
3.如图，位于A处的海面观测站获悉，在其正东方向相距40海里的B处有一艘渔船遇险，并在原地等待营救，在A处南偏西30°且相距20海里的C处有一艘救援船，则该船到救助处B的距离为(   ).

A.2800海里 B.1200海里 C.海里 D.海里

4.在锐角中,角的对边分别为的面积为S,若,则的取值范围为(   )

A. B. C. D.

5.在中,内角所对的边长分别是,若,则的形状为(   )

A.等腰三角形  B.直角三角形

C.等腰直角三角形  D.等腰三角形或直角三角形

6.若两个三角形不在同一平面内，它们的边两两对应平行，则这两个三角形(   )

A.全等 B.相似 C.仅有一个角相等 D.无法判断

7.如图，为了测量某湿地A，B两点间的距离，观察者找到在同一条直线上的三点C，D，E.从D点测得，从C点测得，，从E点测得.若测得，（单位：百米），则A，B两点间的距离为(   )

A. B. C.3 D.

8.（多选）如图，在平面四边形ABCD中，已知，，，，，下列四个结论中正确的是(   ).

A.  B.四边形ABCD的面积为

C.  D.四边形ABCD的周长为

9. （多选）如图，在平滑的固定木板上有三个洞，取三条绳子系于一点O，穿过洞各挂一只猴子玩具，且呈现平衡状态.已知挂在洞下方的猴子玩具的质量分别为分别记作，则下列说法正确的是(   )

A.若，则 B.若，则

C.若，则 D.若，则

10. （多选）在中,已知角A,B,C所对的边分别为a,b,c,且,则以下四个结论正确的有(   )
A.不可能是直角三角形 B.有可能是等边三角形 C.当时, 的周长为15              D.当时, 的面积为

11.在中，角A，B，C所对的边分别为a，b，c，其中，，则的最小值为_____________.

12.如图，在中，，点D在AB的延长线上，，则CD长的最小值为________________.

13.在200米高的山顶上，测得山下一塔顶与塔底的俯角分别为30°，60°，则塔高为_____米.

14.的内角A，B，C的对边分别为a，b，c，已知.

(1)求B.

(2)若为锐角三角形，且，求面积的取值范围.

15.如图，观测站C在目标A的南偏西20°方向，经过A处有一条南偏东40°走向的公路，在C处观测到与C相距31km的B处有一人正沿此公路向A处行走，走20km到达D处，此时测得C，D相距21km，求D，A之间的距离.

答案以及解析

1.答案：A

解析：由正弦定理可得，得.

，，整理得，得B为钝角，

为钝角三角形.

2.答案：A

解析：因为，

所以由正弦定理，可得，

又，所以，

因为，所以，

又因为，所以，所以为直角三角形.故选A.

3.答案：D

解析：由已知得海里，海里，，在中，由余弦定理得（海里）.故选D.

4.答案：A

解析：,即,.由余弦定理,可得.由正弦定理得.又或,解得或(舍).是锐角三角形,解得,由正弦定理得

,故选A.

5.答案：D

解析：由余弦定理得,

,代入原式得,

所以,所以,

解得或,则为等腰三角形或直角三角形.

6.答案：B

解析：由等角定理知，这两个三角形的三个角分别对应相等，所以这两个三角形相似.

7.答案：C

解析：在中，，，则，.在中，，，则，由正弦定理，得.则在中，，，，由余弦定理得，则.故选C.

8.答案：ACD

解析：在中，可得，

在中，可得，

可得，即，

因为，所以，可得，

又因为B为三角形的内角，所以，所以，所以A正确；

因为，所以B不正确；

在中，可得，所以C正确；

四边形ABCD的周长，所以D正确.故选ACD.

9.答案：ABD

解析：设，由题意知，如图，构成三角形，易知A、B正确，对于C，在中，易知，由正弦定理知，C错误.对于D，，所以，即，解得，D正确.故选ABD.

10.答案：CD

解析：由正弦定理得，
对选项A，若A是直角，则，所以存在是直角三角形，故A错误.
对选项B，因为，所以不存在是等边三角形，故B错误.
对选项C，若，则的周长为15，故C正确.
对选项D, ,解得，所以的面积，故D正确,故选CD,

11.答案：8

解析：由题意知，根据正弦定理，可得，

因为，所以，

即，

则，当且仅当时等号成立，

即的最小值为8.

12.答案：

解析：在中，由正弦定理得，，

在中，由余弦定理得，，且，

，的最大值为1，

的最小值为.

13.答案：

解析：如图所示，

山的高度米，塔高为，

所以塔高(米).

14.答案：(1)

(2)

解析：(1)由题设及正弦定理得.

因为，所以.

由，可得，

故.

因为，故，因此.

(2)由题设及(1)知的面积.

由正弦定理得.

由于为锐角三角形，故，

由(1)知，所以，故，

从而.

因此，面积的取值范围是.

15.答案：距离为15km

解析：由已知，得.

在中，.

设，则.

在中，由正弦定理，

得，

所以，

即所求的距离为15km.