中考数学一轮单元复习《视图与投影》夯基练习(2份打包，教师版+原卷版)

中考数学一轮单元复习《视图与投影》

夯基练习

一              、选择题

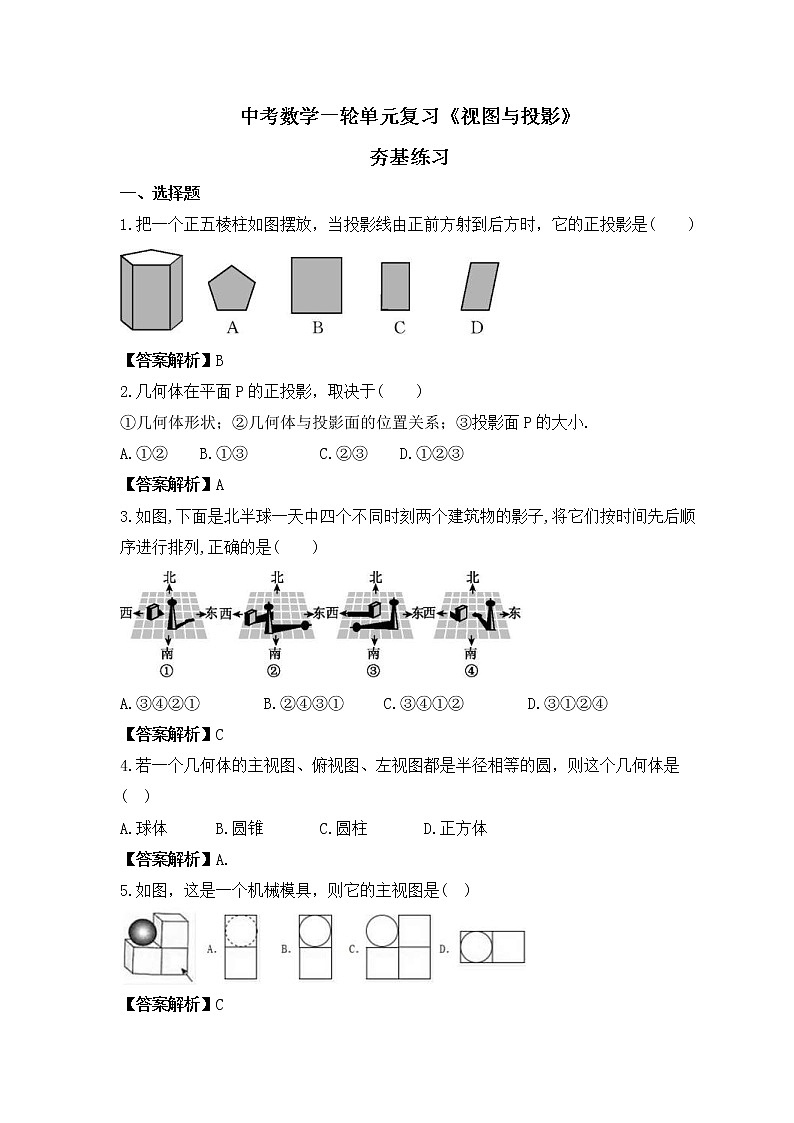
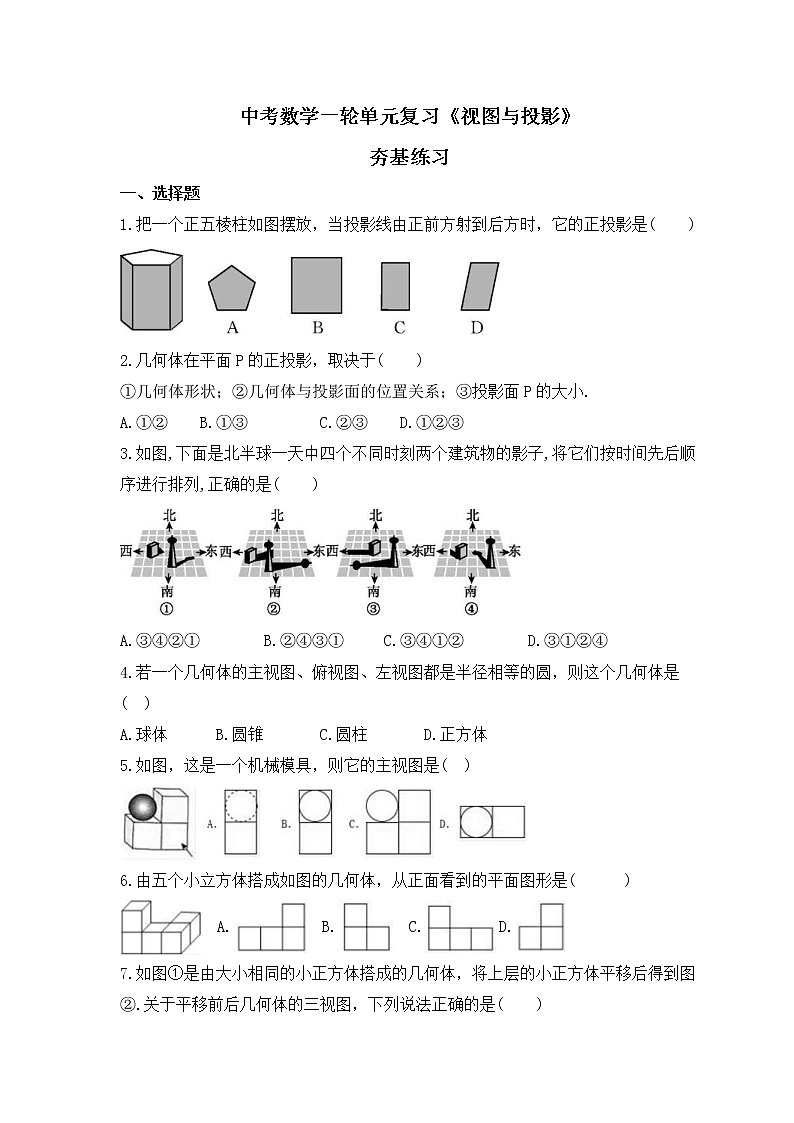
1.把一个正五棱柱如图摆放，当投影线由正前方射到后方时，它的正投影是(　　)

【答案解析】B

2.几何体在平面P的正投影，取决于(　　)

①几何体形状；②几何体与投影面的位置关系；③投影面P的大小.

A.①②                  B.①③         C.②③                  D.①②③

【答案解析】A

3.如图,下面是北半球一天中四个不同时刻两个建筑物的影子,将它们按时间先后顺序进行排列,正确的是(　　)

A.③④②①        B.②④③①     C.③④①②        D.③①②④

【答案解析】C

4.若一个几何体的主视图、俯视图、左视图都是半径相等的圆，则这个几何体是(  )

A.球体      B.圆锥       C.圆柱       D.正方体

【答案解析】A.

5.如图，这是一个机械模具，则它的主视图是(  )

【答案解析】C

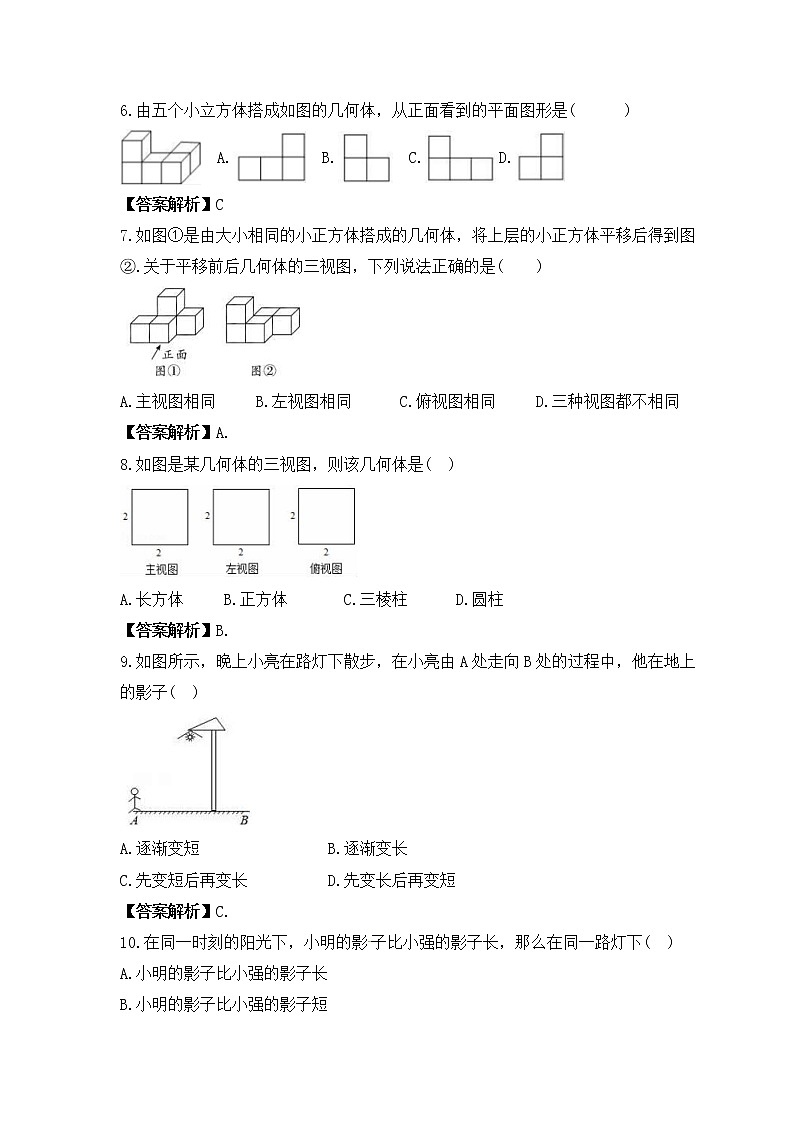
6.由五个小立方体搭成如图的几何体，从正面看到的平面图形是(      )

  A.                B.                C.              D.

【答案解析】C

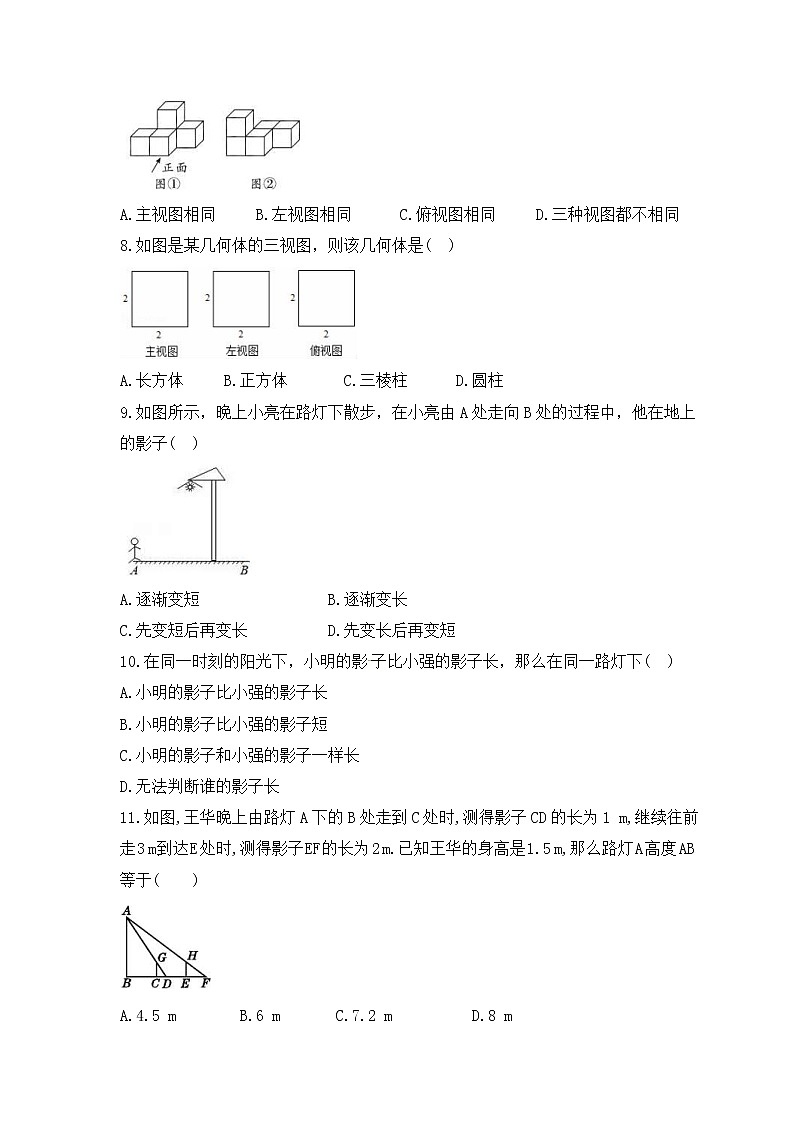
7.如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②.关于平移前后几何体的三视图，下列说法正确的是(    )

A.主视图相同     B.左视图相同      C.俯视图相同     D.三种视图都不相同

【答案解析】A.

8.如图是某几何体的三视图，则该几何体是(  )

A.长方体     B.正方体       C.三棱柱      D.圆柱

【答案解析】B.

9.如图所示，晚上小亮在路灯下散步，在小亮由A处走向B处的过程中，他在地上的影子(  )

A.逐渐变短                B.逐渐变长

C.先变短后再变长          D.先变长后再变短

【答案解析】C.

10.在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下(  )

A.小明的影子比小强的影子长

B.小明的影子比小强的影子短

C.小明的影子和小强的影子一样长

D.无法判断谁的影子长

【答案解析】D.

11.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1 m,继续往前走3 m到达E处时,测得影子EF的长为2 m.已知王华的身高是1.5 m,那么路灯A高度AB等于(　　)

A.4.5 m　    　B.6 m　   　C.7.2 m　      　D.8 m

【答案解析】B

12.我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境：如图，小王从点A经过路灯C的正下方沿直线走到点B，他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系，最有可能与上述情境类似的是(　　)

A.y=x        B.y=x＋3　    C.y=        D.y=(x－3)2＋3

【答案解析】答案为：D.

二              、填空题

13.若干桶方便面摆放在桌子上.实物图片左边所给的是它的三视图.则这一堆方便面共有    桶.

【答案解析】答案为：6.

14.如图是一个长方体的三视图(单位：cm)，根据图中数据计算这个长方体的体积是______cm2.

【答案解析】答案为：24.

15.已知某几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的左视图的面积为　   　．

【答案解析】答案为：(18+2)cm2．

16.直角坐标系内，一点光源位于A(0，5)处，线段CD⊥x轴，垂足为D，C点坐标为(3，1)．则CD在x轴上的影长为         ，点C的影子B的坐标为          ．

【答案解析】答案为：,(，0).

17.某同学想利用影子长度测量操场上旗杆的高度，在某一时刻，他测得自己影子长为0.8m，立即去测量旗杆的影子长为5m，已知他的身高为1.6m，则旗杆的高度为_______m.

【答案解析】答案为：10

18.晚上，小亮走在大街上，他发现当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3 m，左边的影子长为1.5 m.又知自己身高1.80 m，两盏路灯的高相同，两盏路灯之间的距离为12 m，则路灯的高为______ m.

【答案解析】答案为：6.6.

三              、作图题

19.如图，是由一些棱长都为1的小正方体组合成的简单几何体.         

(1)该几何体的表面积(含下底面)为      ；          

(2)请画出这个几何体的三视图并用阴影表示出来；        

(3)如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和俯视图不变，那么最多可以再添加      个小正方体. 

【答案解析】解：(1)(4×2＋6×2＋4×2)×(1×1)=(8＋12＋8)×1=28×1=28.

故该几何体的表面积(含下底面)为2.

(2)如图所示：        

(3)由分析可知，最多可以再添加2个小正方体. 故答案为：28；2.

20.如图所示，有甲、乙两根木杆，甲木杆的影子刚好落在乙杆与地面接触点处.

（1）你能画出此时太阳光线及乙杆的影子吗？（不能画，说明理由；能画，用线段表示影子）

（2）在所画的图形中有相似三角形吗？为什么？

（3）从图中分析高杆与低杆的影子与它们的高度之间有什么关系？与同学进行交流.

【答案解析】解：（1）乙杆的影子如图中BC.

（2）图中存在相似三角形，即△ABC∽△DCE.因为两条太阳光线AB∥DC，两杆AC∥DE.

（3）在同一时刻杆越高，它的影子就越长，反之则短，即影长与杆高成正比.

四              、解答题

21.某工厂要加工一批茶叶罐，设计者给出了茶叶罐的三视图(如图)，请你按照三视图确定制作每个密封罐所需钢板的面积.(单位：mm)

【答案解析】解：由三视图可知茶叶罐的形状为圆柱体，并且茶叶罐的底面直径2R为100 mm，高h为150 mm.

∵每个密封罐所需钢板的面积即为该圆柱体的表面积，

∴S表面=2πR2＋2πRh

=2π×502＋2π×50×150

=20000π(mm2).

答：制作每个密封罐所需钢板的面积为20000π mm2.

22.如图所示是一个几何体的三视图，一只蚂蚁要从该几何体的顶点A处，沿着几何体的表面到和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长度是多少？

【答案解析】解：该几何体为如图所示的长方体.

由图知，蚂蚁有三种方式从点A爬向点B，

且通过展开该几何体可得到蚂蚁爬行的三种路径长度分别为

l1==(cm)；

l2==(cm)；

l3==(cm).

通过比较，得最短路径长度是 cm.

23.地面上直立一根标杆AB，如图，杆长为2 m.

(1)当阳光垂直照射地面时，标杆在地面上的投影是什么图形？

(2)当阳光与地面的倾斜角为60°时，标杆在地面上的投影是什么图形？并画出投影示意图.

【答案解析】解：(1)点.

(2)当阳光与地面的倾斜角为60°时，标杆在地面上的投影是一条线段.图略.

24.为了测量校园内一棵不可攀的树的高度，学校数学应用实践小组做了如下探索：

根据《自然科学》中的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把镜子放在离树（AB）8.7米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.7米，观察者目高CD=1.6米，请你计算树（AB）的高度．（精确到0.1米）

【答案解析】解：由题意知∠CED=∠AEB，∠CDE=∠ABE=90°，

∴△CED∽△AEB.

∴.∴.

∴AB≈5.2米.

答案：AB≈5.2米.

25.如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量：某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.

(1)该小组的同学在这里利用的是          投影的有关知识进行计算的; 

(2)试计算出电线杆的高度,并写出计算的过程.

【答案解析】解：(1)平行

(2)如图,连接AE,CG,过点E作EM⊥AB于M,过点G作GN⊥CD于N,

则MB＝EF＝2,ND＝GH＝3,ME＝BF＝10,NG＝DH＝5.

所以AM＝10-2＝8.

由平行投影可知,＝,即＝,

解得CD＝7.

即电线杆的高度为7米.