

初中数学北师大版九年级下册第一章 直角三角形的边角关系1 锐角三角函数教案
展开1.1 锐角三角函数
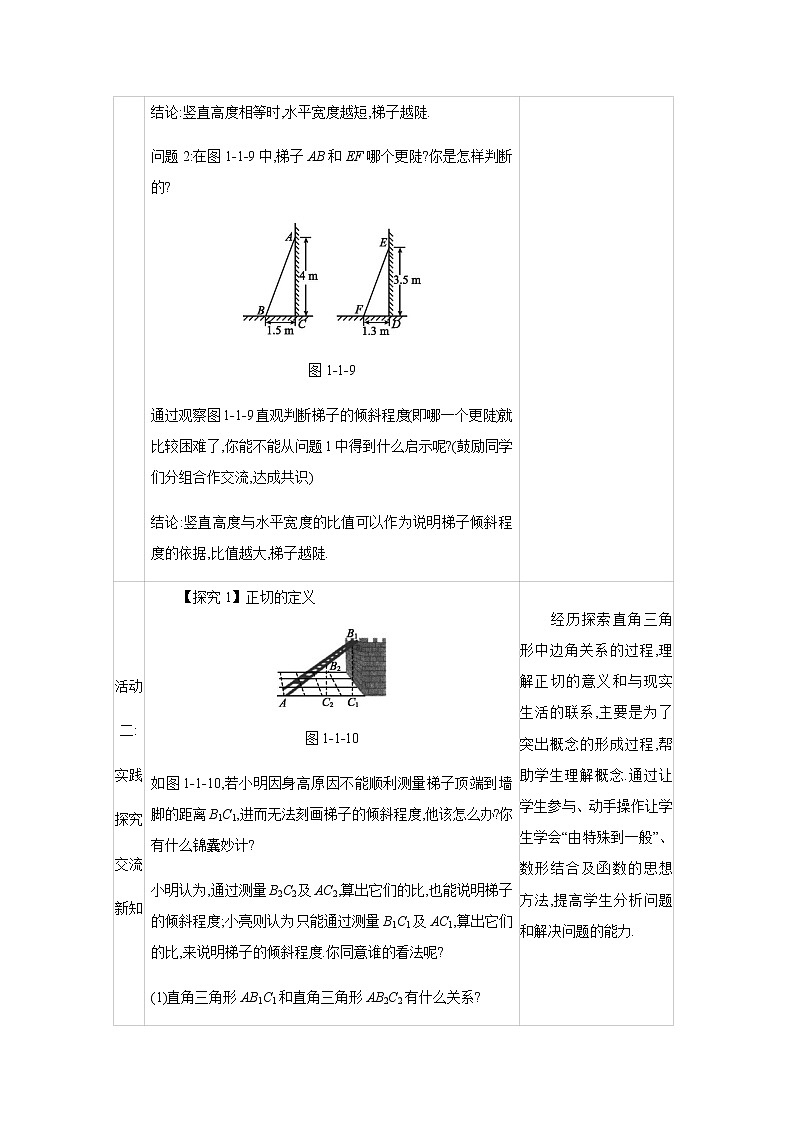
第1课时 正切
教 学 目 标 | 知识技能 | 经历探索直角三角形中边角关系的过程,理解正切的意义和与现实生活的联系. | ||||||||
数学思考 | 能够用tanA表示直角三角形中两直角边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算. | |||||||||
问题解决 | 1.从现实情境中探索直角三角形的边角关系; 2.理解正切、倾斜程度、坡度的数学意义,了解数学与生活的密切联系. | |||||||||
情感态度 | 体验数形之间的联系,逐步学习利用数形结合的思想分析问题和解决问题,提高解决实际问题的能力. | |||||||||
教学 重点 | 掌握正切的定义及基本应用. | |||||||||
教学 难点 | 了解学习正切的必要性,理解正切的大小由角度决定. | |||||||||
教具 | 制作课件,学生课前进行相关预习 | |||||||||
教学活动 | ||||||||||
教学 步骤 | 师生活动 | 设计意图 | ||||||||
回顾 | 直角三角形的三边满足怎样的数量关系?两个锐角满足怎样的数量关系?猜想边和角之间有数量关系吗? | 学生回忆并回答旧知,为本课的学习提供迁移或类比方法. | ||||||||
活动 一: 创设 情境 导入 新课 | 【课堂引入】 图1-1-7 你知道图1-1-7中建筑物的名字吗?是的,它就是意大利著名的建筑——比萨斜塔,是世界著名建筑奇观,位于意大利托斯卡纳省比萨城北面的奇迹广场上,是奇迹广场四大建筑之一,也是意大利著名的标志之一.它从建成之日起便由于土层松软而倾斜,应该如何用数学方法来描述它的倾斜程度呢? | 创设有意义的问题情境,使学生对学习正切的必要性有直观的印象,调动学生的积极性,初步培养建模意识. | ||||||||
活动 二: 实践 探究 交流 新知 | 问题1:在图1-1-8中,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法? 图1-1-8 梯子AB比梯子EF更陡. 方法一:从图中很容易发现∠ABC>∠EFD,所以梯子AB比梯子EF陡. 方法二:因为AC=ED,所以只要比较BC,FD的长度即可判断哪个梯子陡.因为BC<FD,所以梯子AB比梯子EF陡.(比较梯子的底部到墙角的距离来判断) 结论:竖直高度相等时,水平宽度越短,梯子越陡. 问题2:在图1-1-9中,梯子AB和EF哪个更陡?你是怎样判断的? 图1-1-9 通过观察图1-1-9直观判断梯子的倾斜程度(即哪一个更陡)就比较困难了,你能不能从问题1中得到什么启示呢?(鼓励同学们分组合作交流,达成共识) 结论:竖直高度与水平宽度的比值可以作为说明梯子倾斜程度的依据,比值越大,梯子越陡. | 可以让学生独立思考,尽情地发表自己的看法,培养学生独立思考并积极发表自身意见的习惯,而后教师根据学生的想法给予点评. | ||||||||
活动 二: 实践 探究 交流 新知 | 【探究1】正切的定义 图1-1-10 如图1-1-10,若小明因身高原因不能顺利测量梯子顶端到墙脚的距离B1C1,进而无法刻画梯子的倾斜程度,他该怎么办?你有什么锦囊妙计? 小明认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度;小亮则认为只能通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度.你同意谁的看法呢? (1)直角三角形AB1C1和直角三角形AB2C2有什么关系? (2)和有什么关系? (3)如果改变B2在梯子上的位置呢?由此你能得出什么结论? 结论:由相似三角形的对应边成比例,得 =,即=. 如果改变B2在梯子上的位置,总可以得到Rt△AB2C2∽Rt△AB1C1,仍能得到=,因此,无论B2在梯子的什么位置(除点A外),=总成立. 正切的定义:如图1-1-11,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即tanA=. 图1-1-11 注意: 1.tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”. 2.tanA没有单位,它表示一个比值,即直角三角形中∠A的对边与邻边的比. 3.tanA不表示“tan”乘“A”. 4.初中阶段,正切是在直角三角形中定义的,∠A是一个锐角. 【探究2】坡度的定义 生活中,常用一个锐角的正切表示梯子的倾斜程度.正切在日常生活中的应用很广泛,例如建筑、工程技术等;正切也经常用来描述山坡的坡度、堤坝的坡度. 如图1-1-12所示,有一山坡在水平方向上每前进100 m,就升高60 m,那么山坡的坡度(即坡角α的正切——tanα)就是tanα==. 这里要注意区分坡度和坡角.坡面的铅直高度与水平宽度的比(即坡角的正切)称为坡度(或坡比).坡度越大,坡面就越陡. 图1-1-12 | 经历探索直角三角形中边角关系的过程,理解正切的意义和与现实生活的联系,主要是为了突出概念的形成过程,帮助学生理解概念.通过让学生参与、动手操作让学生学会“由特殊到一般”、数形结合及函数的思想方法,提高学生分析问题和解决问题的能力.
由实际生活中的斜坡问题,引出坡度的定义,学生较易接受,同时进一步让学生体会数学与现实生活的联系. | ||||||||
活动 三: 开放 训练 体现 应用 | 【应用举例】 例1 坡度(或坡比)是坡面的 高度(h)与 宽度(l)的比.记作i,即i= ; 坡度与坡角的关系:坡度越大,坡角α就越 ,坡面就越 . 例2 在Rt△ABC中,若∠C=90°,AC=4,BC=2,则tanB= . | 通过例题训练学生对于坡度、正切定义的理解与掌握,既有基本应用,又有反思讨论,螺旋式上升. | ||||||||
【拓展提升】 例3 在△ABC中,∠C=90°,BC=12 cm,AB=20 cm,求tanA和tanB的值.
例4 在△ABC中,∠C=90°,∠ABC=60°,若D是AC边的中点,则tan∠DBC的值为 . 例5 如图1-1-13,某人从山脚下的点A走了130 m后到达山顶的点B,已知点B到山脚的垂直距离为50 m,求山的坡度. 图1-1-13 | 让学生运用新知识解决与直角三角形有关的实际问题,并进一步感受数形结合的思想,体会数形结合的方法,加深学生对正切的理解,正切的前提是必须在直角三角形中. | |||||||||
活动 四: 课堂 总结 反思 | 【当堂训练】 1.课本P4随堂练习 2.课本P4习题1.1中T1、T2、T3 | 当堂检测,及时反馈学习效果. | ||||||||
【板书设计】
| 提纲挈领,重点突出. | |||||||||
【教学反思】 ①[授课流程反思] 在解决实际问题中引发认知冲突,发现已有知识不能直接解决问题,需建立新的模型,通过探究、归纳得出正切的定义,再运用这一定义进行计算加以巩固,整个流程符合学生的认知规律,是一个从已有知识发展出新知识的过程.其中的一个关键是想到用高与宽的比刻画梯子的倾斜程度,这与学生的数学素养关系很大,不同的学生群差别很大,这个设计中没有给出详细的得出过程,可以根据实际情况予以补充. ②[讲授效果反思] ③[师生互动反思] ④[习题反思] 好题题号 错题题号 | 反思,更进一步提升. | |||||||||
导学设计
一、学法点津
学生学习时首先通过情景题了解本节课学习的主要任务,做到有的放矢,然后利用“由一般到特殊”的数学思想,通过三个探究活动逐步得出梯子的倾斜程度与tanA的关系(∠A和tanA之间的关系),在探究过程中,可以通过自主探究与合作交流的方式抓住重点,突破难点.学生在运用正切解决问题时,一定要注意其前提条件——在直角三角形中,找准直角三角形是解题的关键.而有些题目需要作辅助线构造直角三角形,也可以通过角度的转化进行求解,同时还要注意数形结合思想的运用.
二、学点归纳总结
(一)知识要点总结
(1)正切的定义:tanA=;
(2)梯子的倾斜程度与tanA的关系(∠A和tanA之间的关系):tanA的值越大,梯子越陡;
(3)坡度(或坡比)的定义:i=tanα=.
(二)规律方法总结
运用正切进行计算时要找准直角三角形或构造出直角三角形,或者通过角度的转化,并运用数形结合的思想进行解答.
(三)易错问题误区点拨
1.对正切的概念理解不清.
【典例1】把△ABC三边的长度都扩大为原来的3倍,则锐角A的正切值 ( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
【错解】 C
【错解分析】误认为锐角的正切值会随三边长度的扩大而扩大.
【正解】 A
【正解分析】因为△ABC三边的长度都扩大为原来的3倍后,所得到的三角形与原三角形相似,所以锐角A的大小没改变,所以锐角A的正切值也不变.故选A.
2.对所有可能情况考虑不全而出错.
【典例2】已知正方形ABCD的边长为2,P是直线CD上一点,若DP=1,则tan∠BPC的值是 .
【错解】 2
【错解分析】对于条件“P是直线CD上一点”中的“直线”理解不清,往往会只考虑“点P在线段CD上”这一种情况,而忽略“点P在线段CD的延长线上”这一种情况.
【正解】 2或
【正解分析】如图1-1-14,此题有两种可能:
图1-1-14
(1)如图①,∵BC=CD=2,DP=1,∠C=90°,
∴PC=1,∴tan∠BPC==2;
(2)如图②,∵DP=1,DC=2,∴PC=3.
又∵BC=2,∠C=90°,∴tan∠BPC==.
综上所述,tan∠BPC的值是2或.
三、巩固拓展练习
1.如图1-1-15,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tanB的值是 ( C )
图1-1-15
A. B. C. D.
[解析] ∵CD是斜边AB上的中线,CD=5,∴AB=2CD=10.根据勾股定理,得BC===8,∴tanB===.
2.[贵阳中考]如图1-1-16,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于 ( C )
图1-1-16
A. B. C. D.
[解析] 过点P作PE⊥x轴于点E.
∵点P的坐标为(12,5),∴PE=5,OE=12,∴tanα==.故选C.
3.河堤横断面如图1-1-17所示,堤高BC=5米,迎水坡AB的坡度是1∶(坡度是坡面的铅直高度BC与水平宽度AC之比),则AB的长是 10米 .
图1-1-17
[解析] 在Rt△ABC中,BC=5米,tanA=1∶,
∴AC=BC÷tanA=5米,∴AB==10(米).
4.如果一元二次方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,△ABC最小的角为∠A,那么tanA的值为 或 .
[解析] 解方程x2-4x+3=0,得x1=1,x2=3.①当3是直角边长时,∵△ABC最小的角为∠A,∴tanA=;②当3是斜边长时,根据勾股定理,得∠A的邻边长==2,∴tanA==.所以tanA的值为或.
5.如图1-1-18,在锐角三角形ABC中,AB=10 cm,BC=9 cm,△ABC的面积为27 cm2.求tanB的值.
图1-1-18
解:如图1-1-19,过点A作AH⊥BC于点H.
∵S△ABC=27 cm2,∴×9·AH=27,∴AH=6 cm.
∵AB=10 cm,∴BH===8(cm),
∴tanB===.
图1-1-19
四、挑战课标中考
1.[金华中考]如图1-1-20,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是 (C)
图1-1-20
A.1 B.1.5 C.2 D.3
[解析] 如图1-1-21.∵点A(t,3)在第一象限,∴AB=3,OB=t.又∵tanα==,∴t=2.
图1-1-21
[解题策略] 本题考查正切的定义和坐标的意义,解题方法是根据正切的定义列方程求解.易错点是坐标与线段的对应关系以及正切的定义:对边比邻边.
2.[温州中考]如图1-1-22,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 .
图1-1-22
[解析] tanA==.
[解题策略] 本题考查了锐角三角函数定义的应用,注意:在Rt△ABC中,∠C=90°,tanA=.
3.[苏州中考]如图1-1-23,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则tan∠BPC= .
图1-1-23
图1-1-24
[解析] 如图1-1-24,过点A作AE⊥BC于点E.
∵AB=AC=5,∴BE=BC=×8=4,∠BAE=∠BAC.
∵∠BPC=∠BAC,∴∠BPC=∠BAE.
在Rt△BAE中,由勾股定理,得AE===3,∴tan∠BAE==.
[解题策略] 求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系求三角函数值.
学案设计
一、学习目标
1.经历探索直角三角形中边角关系的过程,理解正切的意义和与现实生活的联系;
2.能用表示直角三角形中两直角边的比,表示物体的倾斜程度和坡度(坡比)等;
3.能根据直角三角形的边角关系,用正切进行简单的计算。
二、学习过程
(一)温故知新[来源:学科网]
1.在Rt△ABC中,∠B=53°,∠C=90°,则∠A=;
2.在Rt△ABC中,∠C=90°,BC=24cm,AB=26cm,则AC=;
3.在△ABC中,BC=7cm, AC=24cm,AB=25cm,则△ABC是三角形。
(二)新知探究
请你阅读课本P2至P4,然后完成以下问题:
1.比较梯子的倾斜程度
(1)如图,这里摆放的三对梯子,比较每对梯子中哪一个更陡?梯子的倾斜程度与什么有关?
(2)分别求出每幅图中的与,想一想它们的比值与梯子的倾斜程度有什么关系?
2.直角三角形的边与角的关系
(1)
Rt△AB1C1和Rt△AB2C2有什么关系?
正切的定义
如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边之比便随之确定,这个比叫做∠A的正切(tangent),记作tanA,即tanA=
如图:
斜坡AB的倾斜程度与tanA的关系:AB越陡,tanA的值越;反过来,tanA的值越大,斜坡AB越.
【例题精选】
1 .下图表示两个自动扶梯,哪一个自动扶梯比较陡?
2.如图,在△ACB中,∠C = 90°,AC = 6,求BC、AB的长.
3.如图,在等腰△ABC中,AB=AC=13,BC=10,求tanB.
课堂小结(你学到了什么?)[来源:学科网ZXXK]
1、正切的定义:.
2、斜坡的倾斜程度与tanA的关系(∠A和tanA之间的关系):.
数学九年级下册第一章 直角三角形的边角关系1 锐角三角函数教学设计: 这是一份数学九年级下册<a href="/sx/tb_c102694_t8/?tag_id=27" target="_blank">第一章 直角三角形的边角关系1 锐角三角函数教学设计</a>,共5页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明,归纳结论等内容,欢迎下载使用。
初中7.1 正切第2课时教案设计: 这是一份初中7.1 正切第2课时教案设计,共5页。
苏科版九年级下册7.1 正切第1课时教案: 这是一份苏科版九年级下册7.1 正切第1课时教案,共5页。













