新疆维吾尔自治区乌鲁木齐市第七十中学2021-2022学年九年级上学期期中考试数学试卷（含答案）

2021-2022学年乌鲁木齐市第七十中学九年级上学期期中考试

数学试卷

满分：150分    考试时间：120分钟

注意事项：

1．答题前填写好自己的姓名、班级、考号等信息

2．请将答案正确填写在答题卡上

一、单选题(每小题5分，共45分)

1．下列图形中，既是轴对称图形又是中心对称图形的是　　

A．B． C． D．

2．关于的方程是一元二次方程，则满足（      ）

A． B． C． D．为任意实数

3．用12米长的钢材制成一个矩形画框，使它的面积为5平方米．若设它的一条边长为x米，则根据题意可列出关于x的方程为（        ）

A． B． C． D．

4．对称轴平行于y轴的抛物线过点（1，m），（3，m）两点，则它的顶点横坐标为（  ）

A． B． C． D．

5．某电子厂一月份的产量为200万件，已知第一季度的总产量共729万件．如果平均每月增长率为x，则由题意列方程应为（　　）

A．200（1+x）2=729 B．200+200×2x=729

C．200+200×3x=729 D．200[1+（1+x）+（1+x）2]=  729

6．如图，点B，C，D在⊙O上，,若∠OBC＝50°，则∠BOD的度数是（　　）

A．50° B．60° C．80° D．100°

7．已知点三点都在抛物线的图象上，则的大小关系是（  ）

A． B．＜＜ C．＜＜ D．＜＜

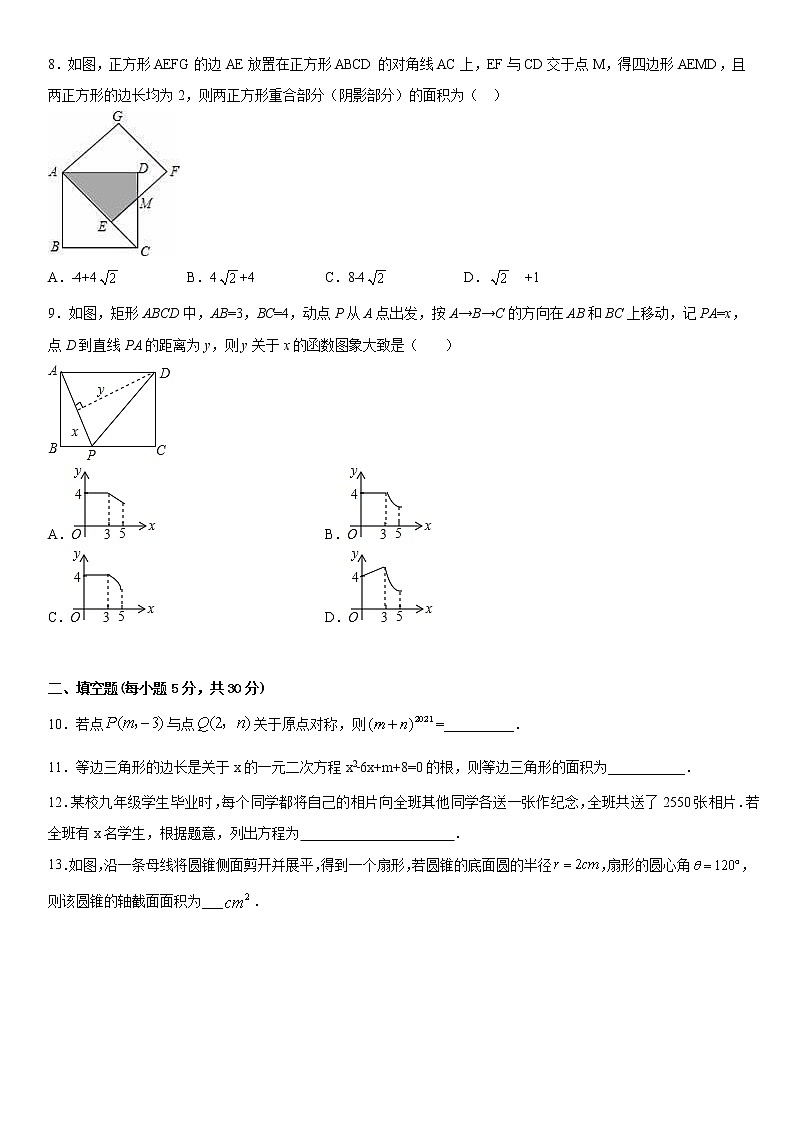
8．如图，正方形AEFG的边AE放置在正方形ABCD的对角线AC上，EF与CD交于点M，得四边形AEMD，且两正方形的边长均为2，则两正方形重合部分（阴影部分）的面积为（  ）

A．﹣4+4 B．4+4 C．8﹣4 D．  +1

9．如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（    ）

A． B．

C． D．

二、填空题(每小题5分，共30分)

10．若点与点关于原点对称，则=__________．

11．等边三角形的边长是关于x的一元二次方程x2﹣6x+m+8=0的根，则等边三角形的面积为___________．

12．某校九年级学生毕业时，每个同学都将自己的相片向全班其他同学各送一张作纪念，全班共送了2550张相片．若全班有x名学生，根据题意，列出方程为                      ．

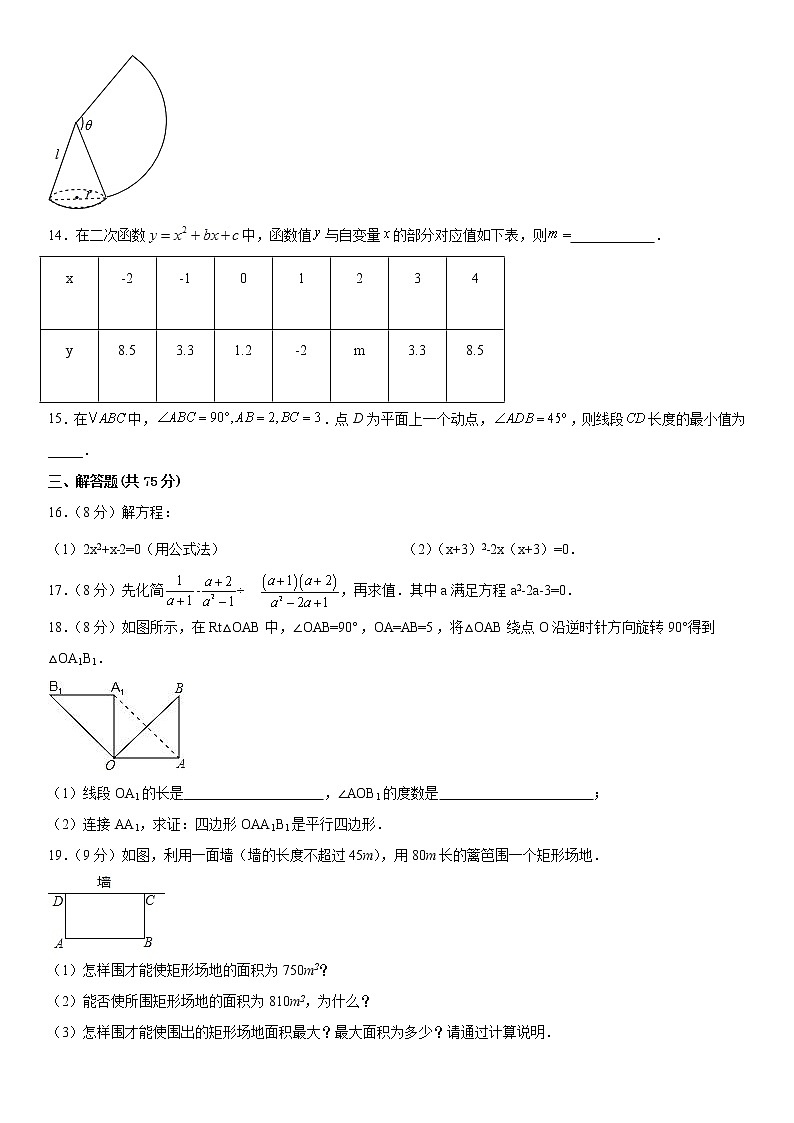
13．如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径，扇形的圆心角，则该圆锥的轴截面面积为___．

14．在二次函数中，函数值与自变量的部分对应值如下表，则=            ．

15．在中，．点D为平面上一个动点，，则线段长度的最小值为_____．

三、解答题(共75分)

16．（8分）解方程：

（1）2x2+x﹣2=0（用公式法）                            （2）（x+3）2﹣2x（x+3）=0．

17．（8分）先化简-÷  ，再求值．其中a满足方程a2-2a-3=0．

18．（8分）如图所示，在Rt△OAB中，∠OAB=90°，OA=AB=5，将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1．

（1）线段OA1的长是                    ，∠AOB1的度数是                      ；

（2）连接AA1，求证：四边形OAA1B1是平行四边形．

19．（9分）如图，利用一面墙（墙的长度不超过45m），用80m长的篱笆围一个矩形场地．

（1）怎样围才能使矩形场地的面积为750m2？

（2）能否使所围矩形场地的面积为810m2，为什么？

（3）怎样围才能使围出的矩形场地面积最大？最大面积为多少？请通过计算说明．

20．（9分）如图，王强在一次高尔夫球的练习中，在某处击球，其飞行路线满足抛物线，其中（m）是球的飞行高度，（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．

（1）请写出抛物线的开口方向、顶点坐标、对称轴．

（2）请求出球飞行的最大水平距离．

（3）若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球飞行路线应满足怎样的抛物线，求出其解析式

21．（10分）某水果商店销售一种进价为40元/千克的优质水果，若售价为50元/千克，则一个月可售出500千克；若售价在50元/千克的基础上每涨价1元，则月销售量就减少10千克．

（1）当售价为55元/千克时，每月销售水果多少千克？

（2）当月利润为8750元时，每千克水果售价为多少元?

（3）当每千克水果售价为多少元时，获得的月利润最大？

22．（10分）如图，BE是圆O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C，

（1）若∠ADE=25°，求∠C的度数；

（2）若AB=AC，CE=2，求⊙O半径的长．

23．（13分）如图，已知抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

（1）若直线y＝mx+n经过B、C两点，求直线BC和抛物线的解析式；

（2）在抛物线的对称轴x＝﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标：

（3）在抛物线上存在点P(不与C重合)，使得△APB的面积与△ACB的面积相等，求点P的坐标．

参考答案：

1．D

2．C

3．B

4．B

5．D

6．D

7．A

8．A

9．B

10．1

11． 

12．x（x﹣1）＝2550

13． 

14．1.2

15．

16．（1），；（2）x1=-3，x2=3.

17．；．

18．（1）5，135°；

（2）证明：

19．（1）当所围矩形的长为30m、宽为25m时，能使矩形的面积为750m2；

（2）不能使所围矩形场地的面积为810m2；

，方程无实数解

（3）当所围矩形的长为40m、宽为20m时，能使矩形的面积最大，最大面积为800  m2．

20．解：

∴抛物线开口向下，顶点为，对称轴为x＝4．

(2)令y＝0，得

解得x1＝0，x2＝8．∴球飞行的最大水平距离是8m．

(3)要让球刚好进洞而飞行最大高度不变，则球飞行的最大水平距离为10m．

∴抛物线的对称轴为x＝5，顶点为

设此时对应的抛物线解析式为

又∵点(0，0)在此抛物线上，

，即

21．（1）450千克；

（2）当月销售利润为元时，每千克水果售价为元或元；

（3）当该优质水果每千克售价为元时，获得的月利润最大

22．（1）∠C=40°；

（2）⊙O的半径为2．

23．（1）y＝﹣x2﹣2x+3，y＝x+3；

（2）点M（﹣1，2）；

（3）点P的坐标为：（﹣2，3）或（，﹣3）或（，﹣3）．