*新阶段学习导入语

“数学是思维的体操”数学活动本质上是一种思维活动.进行思维活动要依据一定的方法.数学方法就其思维方法有抽象和概括、证明、计算、公理法、数学模型法及计算机对数学思想方法的影响等.其中数学建模法是非常重要的数学方法.本章就投资问题，生产安排问题，环境保护问题，混合问题，运输问题和下料问题，师生归纳建立线性规划模型，来解决实际问题.相信同学通过学习线性规划对解决生活中的实际问题有所帮助.

介绍

说明

讲解

倾听

了解

引领

学生

了解新阶段的

数学学习的重点

3

*揭示课题

数学建模法是把实际问题中的有关常量或变量以及它们之间的关系用数学式子表示出来，并加以研究的一种方法，也称数学建模.

这就是我们将要研究学习的5.1线性规划的有关概念.

介绍

说明

了解

引入教学内容

5

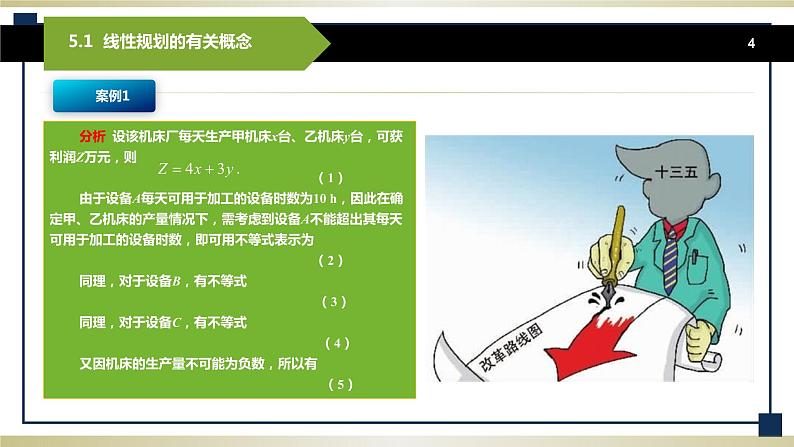
*创设情景 兴趣导入

问题 1

(生产计划问题)某校实习工厂生产A、B两种产品，其成本决定于所用的材料.已知单位产品所需材料量、材料日供应量及单价如表5.1所示.若生产A或B产品的一个单位，所需生产费用同为30元，又A、B的每个单位销售价分别为120元和150元.问：工厂应该如和按排生产，才能使所获得总利润最大？

表5.1

解决

（1）          计算A;B产品单位材料成本所用三种材料价格的和：

      A产品：

      B产品：

（2）          计算A、B产品的单位利润：

（单位利润=销售价—材料成本—生产费用）

A产品的单位利润：

 B产品的单位利润：

（3）          函数的思想：设工厂日产A；B产品分别为单位，可获得的总利润为元.则：

（4）          思考限制产量的条件：

      a材料：≤180.

      a材料：≤400.

      c材料：≤210.

另外：因为产品的生产量不可能为负，则

      ≥0；≥0.

（5）          求获得最大总利润（在满足限制条件下Z的最大值）.即

归纳

第一步：分析题意，通过表格找出量与量之间的关系，

用方程的思想确定决策变量.

     第二步：用函数思想写出目标函数.

     第三步：思考并写出约束条件.

     第四步：求满足约束条件的目标函数的最值.

播放

课件

引导

分析

观看

课件

思考

自我

建构

为决策变量

Z关于间的函数式为目标函数

不等式组为约束条件

从实际问题出发，学生自然

的学习知识点

启发学生分析材料成本；生产费用；单位利润；总利润之间的关系

通过问题1归纳总结解决问题的步骤

10

15

*动脑思考 探索新知

概念

问题1中，两种产品的日生产量叫做决策变量.不等式组叫做约束条件.约束条件中变量的次数都是1次时叫做线性约束条件.关于的函数式叫做目标函数.

问题 2

炼钢厂生产某种钢材，以甲、乙两种型号的废钢为原料，要求元素A、B含量分别不少于10个单位和9个单位.已知甲、乙两种型号的废钢每吨价格分别为400元和500元，且每吨废钢中元素A、B的含量如表5.2所示.考虑在保证钢材质量的条件下，需要甲、乙两种型号的废钢各多少吨时才能使费用最省？试写出线性约束条件和目标函数.

表5.2

解决

第一步：用方程的思想设需要甲、乙两种型号的废钢分别为吨吨.

第二步：用函数思想写出目标函数.设材料总费用为Z,则

第三步：思考并写出约束条件.

第四步：求满足约束条件的目标函数的最值.

归纳

第一步：设未知数确定决策变量.

第二步：列不等式（组）写出约束条件

第三步：选函数最值列出目标函数

*动脑思考 探索新知

概念

求目标函数在约束条件下的最大值或最小值的问题，叫做线性规划问题.满足约束条件的解叫做可行解.由所有的可行解构成的集合叫做可行域.在可行域中，能使目标函数Z取得最大值或最小值的解叫做最优解.

巩固知识 典型例题

例1某工厂用钢与橡胶生产3种产品A、B、C,有关资料如表5.3所示.已知每天可获得100单位的钢和120单位的橡胶，问每天应按排生产A、B、C三种产品各多少，能使总利润最大？试写出问题的线性约束条件和目标函数.

表5.3

解

每天应安排生产A、B、C,三种产品分别为个单位.

则可得约束条件

目标函数为

例2  某工厂生产甲、乙两种产品，每件甲产品要消耗钢材2kg,煤2kg,产值为120元；每件乙产品要消耗钢材3kg,煤1kg,产值为100元；现工厂有钢材600kg., 煤400kg,试确定甲、乙两种产品各生产多少件，才能使该厂的总产值最大？试写出问题的线性约束条件和目标函数.

分析：依据题意列表

解

设甲、乙两种产品的产量分别为

则可得约束条件

目标函数为

总结

归纳

讲解

说明

强调

分析

讲解

提问

归纳

步骤二与步骤四综合成一步

引导

讲解

强调

讲解

鼓励学生自己分析

理解

领会

记忆

思考

回答

明确

思考

理解

领会

归纳

领会

思考

理解题意

思考解题

带领

学生

理解

概念

为后

续学

习做

准备

通过

问题2

进一

步强化解题步骤

观察

学生

是否

理解

知识

点

引领学生归纳解题步骤

教师讲解概念学生领会为后

续学习做准备

强化解题步骤

鼓励学生自己分析鼓励学生自己分析

18

25

30

45

55

*运用知识 强化练习  

练习5.1

某工厂生产甲、乙两种畅销产品，已知计划期具备的资源为钢材3 600kg、电力2 000kw·h,每生产1kg甲、乙两种产品的主要消耗量和单位产品利润如下表所示.问甲、乙两种产品各需生产多少千克，才能在现有条件下获得最大利润？写出问题的线性约束条件和目标函数.

提问

巡视

指导

思考

动手

求解

交流

及时

了解

学生

知识

掌握

情况

75

*理论升华 整体建构

本次课重点学习了线性规划问题的有关概念，能对简单的实际问题进行分析并建立线性规划模型.

第一步：设未知数确定决策变量.

第二步：列不等式（组）写出约束条件

第三步：选函数最值列出目标函数

三步走写出问题的线性约束条件和目标函数.

总结

归纳

理解

体会

从整体再一次

突出三步走解题方法

80

*归纳小结 强化思想

本次课学了哪些内容？重点和难点各是什么？

（1）本次课学了哪些内容？

（2）通过本次课的学习，你会解决哪些新问题了？

（3）在学习方法上有哪些体会？

引导

提问

回忆

反思

培养

学生

总结

学习

过程

能力

88

*继续探索 活动探究

(1)阅读理解： 教材5.1，学习与训练5.1；

(2)书面作业： 教材习题5.1，学习与训练5.1训练题；

(3)实践调查： 探究生活中的应用线性规划问题的实例

说明

记录

90