高中数学人教版（中职）基础模块上册5.1 角的概念的推广及其度量集体备课ppt课件

这是一份高中数学人教版（中职）基础模块上册5.1 角的概念的推广及其度量集体备课ppt课件，文件包含人教版中职数学基础模块上册51《角的概念的推广及其度量》课件ppt、人教版中职数学基础模块上册51《角的概念的推广及其度量》优秀教案doc等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。

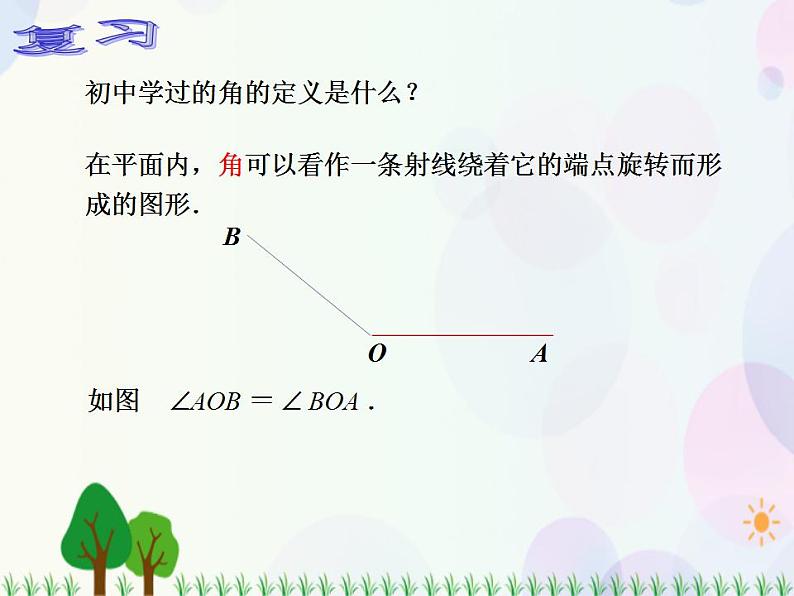
在平面内，角可以看作一条射线绕着它的端点旋转而形成的图形．
初中学过的角的定义是什么？
如图 AOB ＝  BOA ．
如何描述链球转过的角度的大小和方向呢？
体育课上同学们在扔链球.
按逆时针方向旋转所形成的角叫做正角；
按顺时针方向旋转所形成的角叫做负角；
当一条射线没有作任何旋转时叫做零角.
角可以记作角  或   ，也可简记为  .
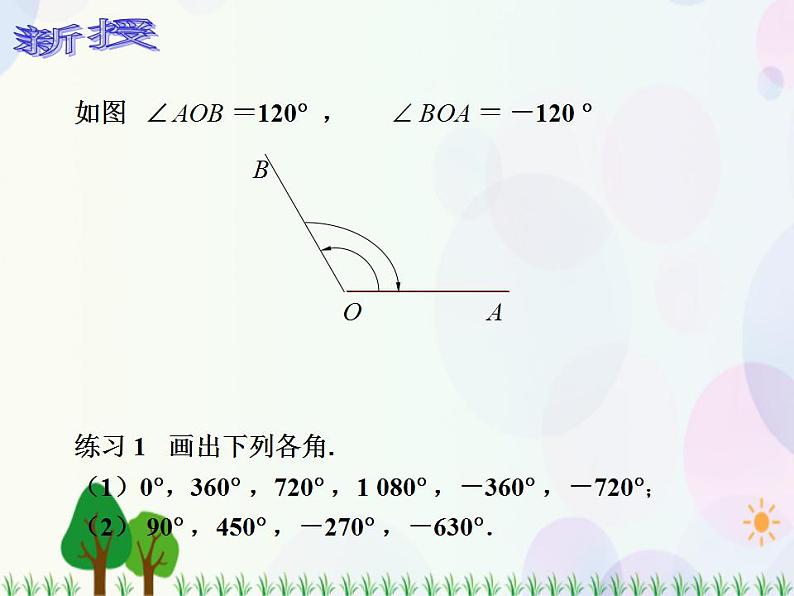
如图  AOB ＝120 ，
 BOA ＝ －120 
练习 1 画出下列各角.（1）0，360 ，720 ，1 080 ，－360 ，－720；（2） 90 ，450 ，－270 ，－630．
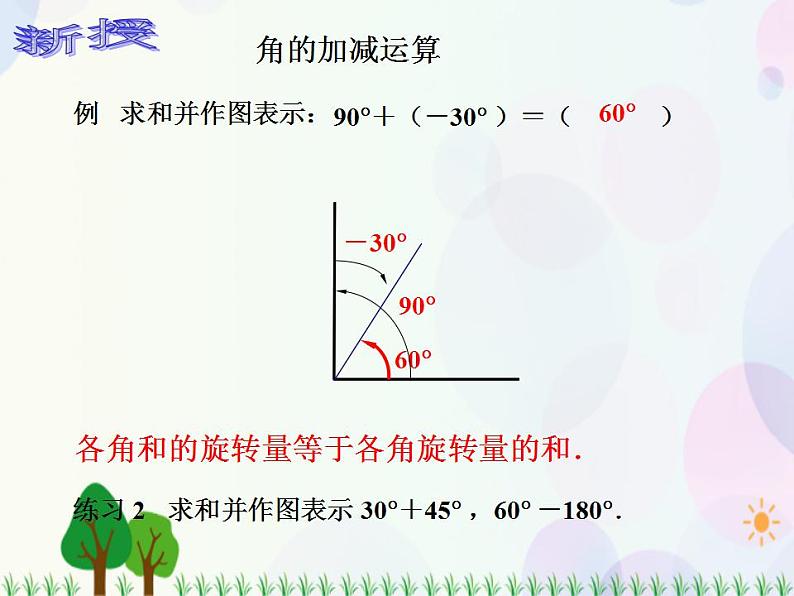
例 求和并作图表示：
90＋（－30 ）＝（ ）
各角和的旋转量等于各角旋转量的和．
练习 2 求和并作图表示 30＋45 ，60 －180．
终边相同的角之间的关系
结论 所有与  终边相同的角构成一个集合：
注意 (1) k  Z； (2)  是任意角； (3) 终边相同的角不一定相等，　　　　 但相等的角终边相同； (4) 终边相同的角有无数多个， 它们的差是 360 的整数倍．
S＝{ |  ＝＋k360，k  Z }
例1（1） 写出与下列各角终边相同的角的集合．
（1）45； （2）135； （3）240； （4）330．
处于标准位置的角的终边落在第几象限，就把这个角叫做第几象限的角．如果角的终边落在坐标轴上，就认为这个角不属于任何象限．
例  是第一象限角， 是第二象限角， 不属于任何象限．
在直角坐标系中讨论角时，通常使角的顶点和坐标原点重合，角的始边与x轴的正半轴重合.这样角的大小和方向可确定终边在坐标系中的位置.这样放置的角，我们说它在坐标系中处于标准位置．
例1（2） 指出下列各角分别是第几象限的角.
例2 写出终边在 y 轴上的角的集合.
试一试 : 写出终边在 x 轴上的角的集合．
例3 在0～ 360 内，找出与下列各角终边相同的角， 并判断它是哪个象限的角． (1) －120； (2) 640； (3) －950．
解 (1) 因为 －120 ＝－360＋240，
所以 240 的角与－120的角终边相同，它是第三象限角．
(2) 因为 640＝360＋280，
所以 280 的角与640的角终边相同，它是第四象限角．
(3)因为－950＝－3×360＋130，
所以 130的角与－950的角终边相同，它是第二象限角．
例4 写出第一象限角的集合.
解 在0～ 360 之间，第一象限角的取值范围是 0＜ ＜90， 所以第一象限角的集合是
{ | k·360 ＜＜90＋k·360，kZ}．
试一试: （1）写出第二象限角的集合； （2）写出第三象限角的集合； （3）写出第四象限角的集合.
1. 锐角是第一象限角.　　　　　　　　(　　 )　　　　　　　
2. 第一象限的角全是锐角. ( 　 )
5. 小于 90 的角都是锐角. 　 ( 　 )
4. 终边相同的角一定相等. ( 　 )
3. 第一象限的角都是正角. ( 　 )
6.小于 90 的角不都是正角. 　 ( 　 )
共同回顾：1. 任意角的概念． 2. 角的合成运算． 3. 终边相同的角的表示方法． 4. 象限角的概念与表示方法．