北师大版（2021）拓展模块一 下册7.1.1 复数的有关概念获奖ppt课件

这是一份北师大版（2021）拓展模块一 下册7.1.1 复数的有关概念获奖ppt课件，文件包含北师大版《中职数学拓展模块一下册》第1课复数的有关概念课件pptx、北师大版《中职数学拓展模块一下册》第1课复数的有关概念教学设计docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

我们知道，在实数集R 的范围内，此方程没有解.
（1）i 的平方等于-1，即i2=-1 ；（2）i 与实数进行四则运算时，原有的加法和乘法运算律仍然成立.
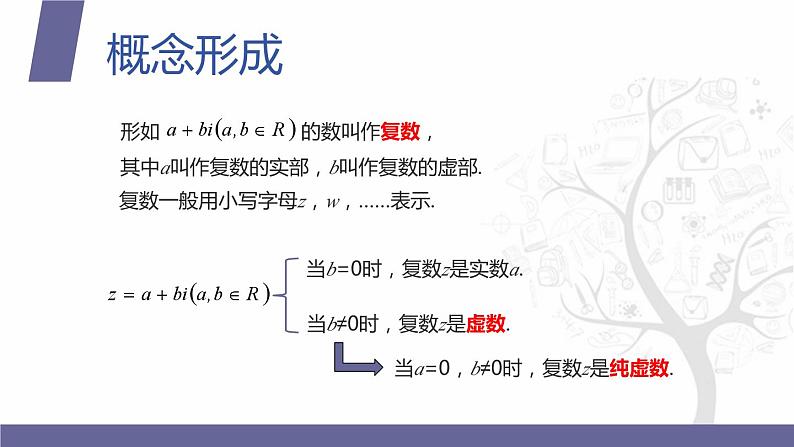
复数一般用小写字母z，w，……表示.
其中a叫作复数的实部，b叫作复数的虚部.
当b=0时，复数z是实数a.
当b≠0时，复数z是虚数.
当a=0，b≠0时，复数z是纯虚数.
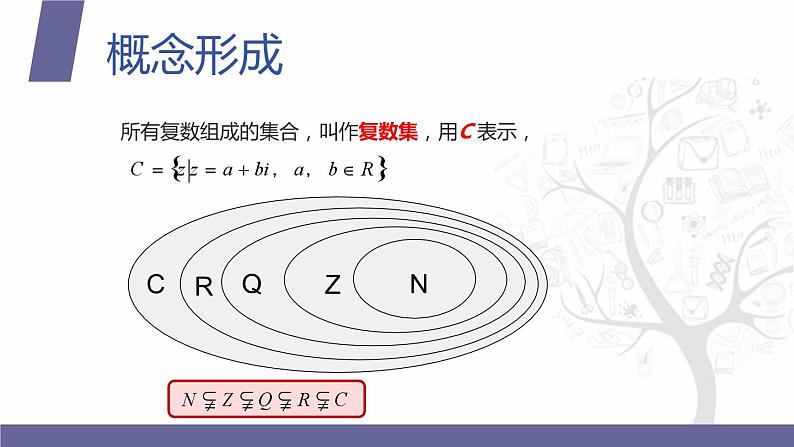
所有复数组成的集合，叫作复数集，用C 表示，
如果两个复数的实部相等且虚部互为相反数，那么称这两个复数互为共轭复数，
例1 指出下列各数中，哪些是实数，哪些是虚数.
复数集C 与实数集R 有一些不同的性质. 例如，任意两个实数是可以比较大小的，而两个复数若不全是实数，则是不能比较大小的.
例2 指出下列复数的实部和虚部.
同桌两人，一人给出一个复数，看谁能又快又准地说出对方所给复数的实部和虚部.
【分析】由复数相等的定义可知，两个复数相等是指这两个复数的实部和虚部分别相等.
根据复数相等的定义，得
【分析】由共轭复数的定义可知，互为共轭复数的两个复数，它们的实部相等且虚部互为相反数.
例4 分别求复数 的共轭复数.
根据共轭复数的定义，得
1. 指出下列复数的实部和虚部，并判定它们是实数还是虚数. 如果是虚数，是否是纯虚数？
2. 求下列各式中 x 与 y 的值.
（1）根据复数相等的定义，得
（2）根据复数相等的定义，得
（3）根据复数相等的定义，得
3. 指出下列复数的共轭复数.
4. 已知复数 是复数 的共轭复数 ，求实数a与b的值 .
根据共轭复数的定义，得
4. 如果两个复数的实部相等且虚部互为相反数，那么称这两个复数互为共轭复数，
课后习题7.1/1-5