*新阶段学习导入语

建立了线性规划问题的数学模型后，下一步如何求出变量的值，使它们既满足线性约束条件，又能使目标函数达到最大值或最小值，即找出线性规划问题的最优解呢？

讲解

说明

倾听

教师指明学习的重点

3

*揭示课题

了 本节内容大纲要求“了解图解法解二元线性规划问题的方法”.

法通过对图解法解线性规划问题的学习,培养学生的作图能力和对

图象的观察能力.

这就是我们将要研究学习的5.2.1 二元一次不等式（组）表示的平面区域.

介绍

说明

了解

引入教学内容

5

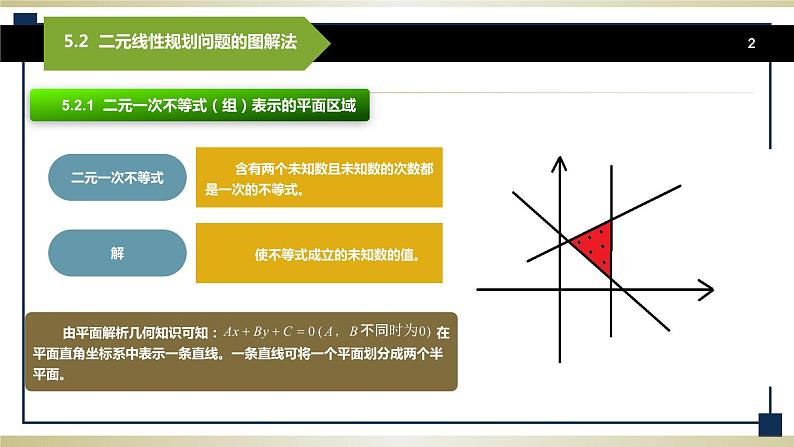
*创设情景 兴趣导入

5.2.1 二元一次不等式（组）表示的平面区域.

我们已经知道，含有两个未知数，并且未知数的次数都是一次的不等式叫做二元一次不等式，使不等式成立的未知数的值叫做它的解.

在上节问题2中，我们看到约束条件中有不等式

≥10，≥9.

由平面解析几何知识可以知道(不同时为0）在平面直角坐标系中表示一条直线.一条直线将一个平面划分成两个半平面.

现考察≤0（或）≥0的几何意义.

巩固知识 典型例题

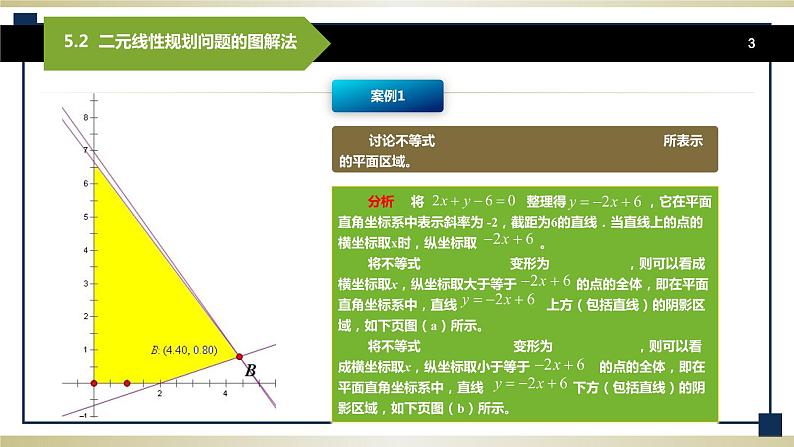
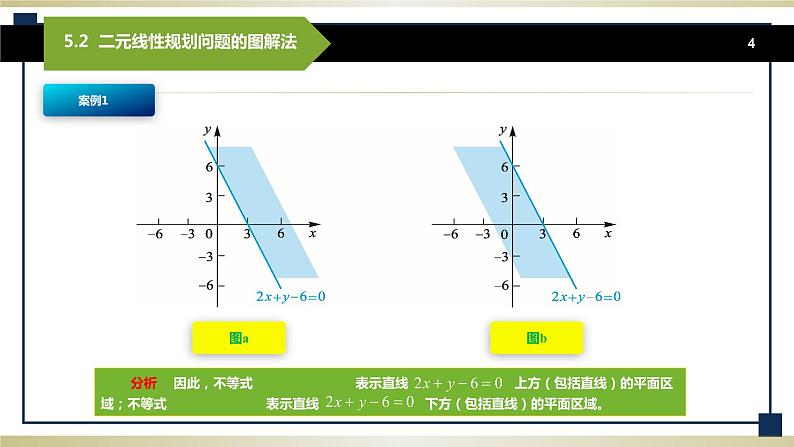
例1 在平面直角坐标系中，指出≤500所表示的区域.

解 将整理，得，它在平面直角坐标系中表示斜率为，截距为125的直线.当该直线上的点的横坐标取时，纵坐标取.

于是≤可以看作横坐标取，纵坐标取小于等于的点的全体.在平面直角坐标系中，表示直线下方（包括直线）的阴影区域如图5-1所示.即≤500表示直线下方（包括直线）的阴影区域.

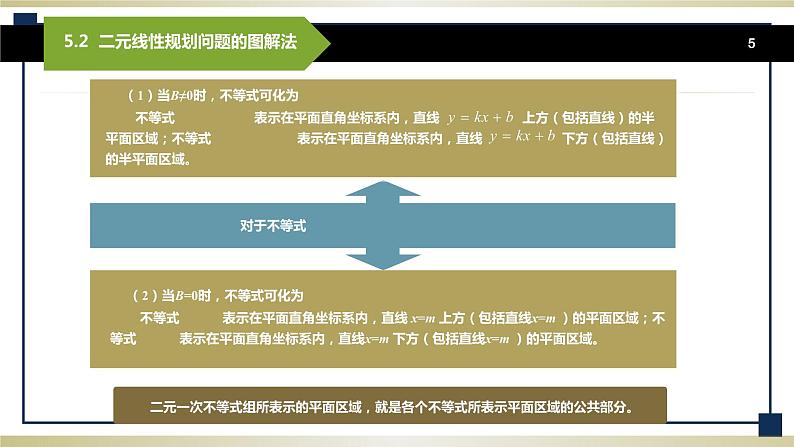
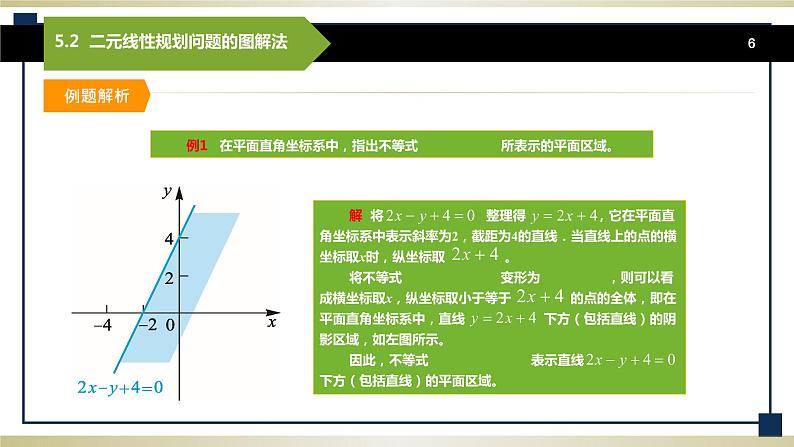
     图5-1                  图5-2 

例2 在平面直角坐标系中，指出≥0所表示的区域.

解 将整理，得，在平面直角坐标系中表示斜率为2，截距为4的直线。该直线上的点的横坐标取时，纵坐标取.

于是y≤2x+4可以看作横坐标取，纵坐标取小于等于的点全体.在平面直角坐标系中表示直线及其下方的阴影区域.即2x-y+4≥0表示直线及其下方的阴影区域，如图5-2所示.

归纳

由例1、例2可以看出≤0（或≥0

）的几何意义：

（1）当时，不等式可化为≥或≤.

表示平面直角坐标系内,在直线上方（包括直线）的半平面区域；≤表示平面直角坐标系内，在直线下方（包括直线）的半平面区域;

（2）当时，不等式可化为x≥m或x≤m它们分别表示在平面直角坐标系内,在直线右方,或在直线x=m左方（包括直线）的平面区域；

对于一元二次不等式组所表示的平面区域，那就是各个不等式所表示的平面区域的公共部分.

例如由约束条件（决策变量分别为

图5-3

所表示的在平面直角坐标系内的区域，是由直线9x+4y=360,4x+5y=200,3x+10y=300以及两条坐标轴所围成的阴影部分（含边界直线）如图5-3所示.

播放

课件

引导

分析

引导学生

理解二元一次不等式（组）表示的平面区域

指导学生完成不等式组的表示的图像

观看

课件

思考

自我

建构

通过分析解决例题

理解二元一次不等式（组）表示的平面区域

在教师的指导下画出图像

讲解

例题学生学习知识点

理解二元一次不等式（组）表示的平面区域

归纳总结解决理解二元一次不等式（组）表示的平面区域

实际操作

10

20

35

45

*动脑思考 探索新知

概念

（1）含有两个未知数，并且未知数的次数都是一次的不等式叫做二元一次不等式，使不等式成立的未知数的值叫做它的解.

（2）二元一次不等式：≤0（或≥0

）的几何意义：

5.2.2 图解法

例3 试解二元线性规划:

约束条件

目标函数

             图 5-4

解  在平面直角坐标系中，分别作出约束条件中各不等式对应的平面区域，满足线性约束条件的点集是由四个半平面区域的公共部分组成（图5-4中的阴影部分）

图5-4中阴影区域（包括边界）上任何一点的都能满足四个不等式；反之，阴影区域外任一点，其坐标都不能同时满足这四个不等式.因此，阴影区域（包括边界）内每一点的坐标都是这个线性规划问题的可行解，所有可行解的全体就构成了这一线性规划问题的可行域.

现在要在可行域中找出一个使目标函数取得最大值的解,即最优解.

观察目标函数的可能取值，不妨令，则得到一条直线这条直线上任何一点都能使得目标函数取同一个常数值（此时=0），将这条直线叫做等值线.分别令等于1，2，…，就可以做出互相平行的直线族.从图5-4中可以看到，当得值增加时，等值线就离原点O越来越远.于是，这个问题转化为：在上述等值线的平行直线族中，找出一条直线，使它既与阴影区域相交，又离开直线最远.由图5-4可见，经过A的等值线符合这一要求.

为求点A的坐标，解方程组               得点A的坐标为（0.5，1.5）.

所以当=0.5， =1.5时，目标函数Z取得最大值

答 问题的最优解是=0.5，=1.5时Zmax=5

归纳

利用图解法解线性规划问题的步骤是：

（1）确定决策变量，列出线性约束条件与目标函数；

（2）由线性约束条件，在平面直角坐标系中画出可行域；

（3）过原点作出目标函数的0等值线，即目标函数值等于0的直线；

（4）将0等值线平行移动，观察确定可行域内最大解的位置，一般最优解在可行域的顶点取得.

（5）求最值——将最优解带入目标函数求值.

例4解第5.1节中的问题2.求满足下面约束条件的目标函数的最小值.

约束条件：

目标函数：

解 作出可行域，如图5-5所示.

图5-5

作出目标函数的0等值线.即.将0等值线向可行与平行移动至点处，这时目标函数取最小值.

解方程组   得点A的坐标为（3，2）

所以当=3，=2时目标函数Z取得最小值

=400×3+500×2=2 200.

答 问题的最优解为甲、乙两种型号的废钢分别用3吨和2吨时，可使总费用最小，其最小费用为2 200元.

总结

归纳

分析

讲解

教师引导

讲解

强调

讲解

鼓励学生自己分析

理解

领会

记忆

思考

回答

理解题意

思考

理解

领会

归纳

领会

思考

理解题意

思考解题

带领

学生

理解

概念

为后

续学

习做

准备

引领学生理解解题意

鼓励学生自己分析鼓励学生自己分析

归纳解题步骤

强化解题步骤

55

65

80

*运用知识 强化练习

练习5.2.2用图解法解5.1节中的例2

例2某工厂生产甲、乙两种产品，每件甲产品要消耗钢材2kg,煤2kg,产值为120元；每件乙产品要消耗钢材3kg,煤1kg,产值为100元；现钢厂有钢材600kg., 煤400kg,试确定甲、乙两种产品各生产多少件，才能使该厂的总产值最大？试写出问题的线性约束条件和目标函数.

提问

巡视

指导

思考

动手

求解

交流

及时

了解

学生

知识

掌握

情况

85

*理论升华 整体建构

本次课重点学习了图解法解线性规划问题. 二元一次不等式（组）所表示的区域就是各不等式所表示区域的公共部分. 、在用图解法解线性规划问题时，我们发现线性规划问题的可行域是一个凸多边形（或凸的区域），（所谓凸的区域，是指若有任意两点在区域内，那么这两点所连线段也在该区域内.）从而使问题的最优解可在凸多边形的顶点处找到，因此，我们也可以通过比较各顶点处目标函数的值求出最优解.

图解法解线性规划问题只限于只有两个决策变量的情形.当多于两

个决策变量的问题，一般不便于用图解法，因此图解法有很大的

局限性.

利用图解法解线性规划问题的步骤是：

（1）确定决策变量，列出线性约束条件与目标函数；

（2）由线性约束条件，在平面直角坐标系中画出可行域；

（3）过原点作出目标函数的0等值线，即目标函数值等于0的直线；

（4）将0等值线平行移动，观察确定可行域内最大解的位置，一般最优解在可行域的顶点取得.

（5）求最值——将最优解带入目标函数求值

总结

归纳

理解

体会

从整体再一次

突出五步走解题方法

*归纳小结 强化思想

本次课学了哪些内容？重点和难点各是什么？

（1）本次课学了哪些内容？

（2）通过本次课的学习，你会解决哪些问题了？

（3）在学习方法上有哪些体会？

引导

提问

回忆

反思

培养

学生

总结

学习

过程

能力

88

*继续探索 活动探究

(1)阅读理解： 教材5.2，学习与训练5.2；

(2)书面作业： 教材习题5.2，学习与训练5.2训练题；

(3)实践调查： 探究生活中的应用线性规划问题的实例

说明

记录

90