安徽省滁州市定远县第一初级中学2022-2023学年八年级上学期第一次月考数学试卷(含答案)

2022-2023学年安徽省滁州市定远一中八年级（上）第一次月考数学试卷

一、选择题（本大题共10小题，每小题4分，满分40分，每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的）

1．（4分）在平面直角坐标系中，点的坐标为，则点在　　

A．第一象限 B．第二象限 C．第三象限 D．第四象限

2．（4分）在函数中，自变量的取值范围是　　

A． B． C． D．

3．（4分）球的体积是，球的半径为，则，其中变量和常量分别是　　

A．变量是，；常量是， B．变量是，；常量是 

C．变量是，，；常量是 D．变量是，；常量是

4．（4分）已知函数是关于的正比例函数，则关于字母、的取值正确的是　　

A．， B．， C．， D．，

5．（4分）如图，象棋盘上，若“将”位于点，“车”位于点，则“马”位于　　

A． B． C． D．

6．（4分）一次函数的图象如图所示，则关于的方程的解为　　

A． B． C． D．

7．（4分）八（1）班同学参加社会实践活动，在王伯伯的指导下，要围一个如图所示的长方形菜园，莱园的一边利用足够长的墙，用篱笆围成的另外三边的总长恰好为，设边的长为，边的长为．则与之间的函数表达式为　　

A． B． 

C． D．

8．（4分）关于一次函数的图象，下列说法不正确的是　　

A．直线不经过第三象限 B．直线经过点 

C．直线与轴交于点 D．随的增大而增大

9．（4分）直线和在同一平面直角坐标系中的图象可能是　　

A． B． 

C． D．

10．（4分）如图，一次函数的图象与轴、轴分别相交于点，，若点在三角形的内部，则的取值范围是　　

A． B． C． D．

二、填空题（本大题共4小题，每小题5分，满分20分）

11．（5分）点到轴的距离为4，到轴的距离为5，且点位于第三象限，则点的坐标为 　　．

12．（5分）点在函数的图象上，则代数式的值等于 　　．

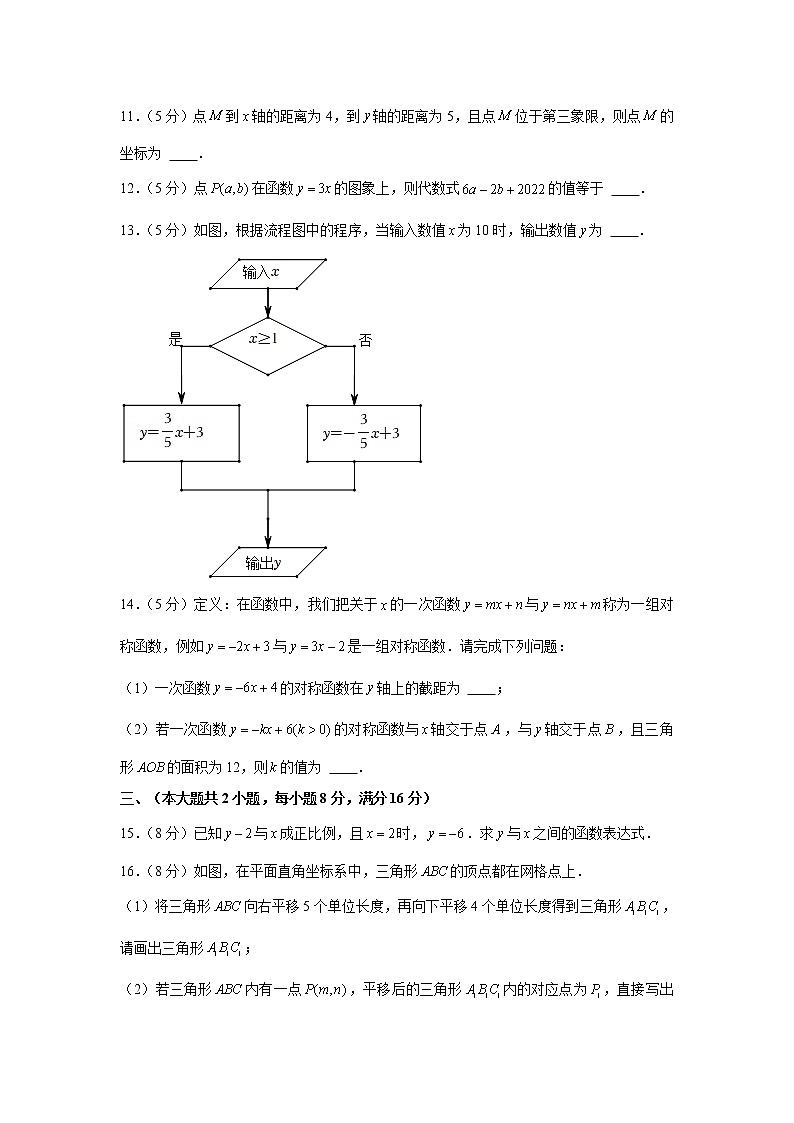
13．（5分）如图，根据流程图中的程序，当输入数值为10时，输出数值为 　　．

14．（5分）定义：在函数中，我们把关于的一次函数与称为一组对称函数，例如与是一组对称函数．请完成下列问题：

（1）一次函数的对称函数在轴上的截距为 　　；

（2）若一次函数的对称函数与轴交于点，与轴交于点，且三角形的面积为12，则的值为 　　．

三、（本大题共2小题，每小题8分，满分16分）

15．（8分）已知与成正比例，且时，．求与之间的函数表达式．

16．（8分）如图，在平面直角坐标系中，三角形的顶点都在网格点上．

（1）将三角形向右平移5个单位长度，再向下平移4个单位长度得到三角形，请画出三角形；

（2）若三角形内有一点，平移后的三角形内的对应点为，直接写出点的坐标：　　．

四、（本大题共2小题，每小题8分，满分16分）

17．（8分）已知是的一次函数，且当时，；当时，．

（1）求这个一次函数的表达式；

（2）当时，直接写出函数的取值范围，

18．（8分）在平面直角坐标系中，点从原点出发，沿轴正方向按折线不断向前运动，其移动路线如图所示．这时点，，，的坐标分别为，，，，，按照这个规律，解决下列问题：

（1）写出下列点的坐标：　　，　　，　　，　　；

（2）点和点的位置分别在 　　，　　．（填轴上方、轴下方或轴上）

五、（本大题共2小题；每小题10分，满分20分）

19．（10分）在平面直角坐标系中，已知点，试分别根据下列条件，求出点的坐标．

（1）点的纵坐标比横坐标小2．

（2）点到两坐标轴的距离相等．

20．（10分）如图1所示，某乘客乘高速列车从甲地经过乙地到丙地，假设列车匀速行驶．如图2所示的是列车离乙地路程（千米）与列车从甲地出发后行驶时间（时之间的函数关系图象．

（1）甲、丙两地间的路程为 　　千米，从甲地到丙地共用 　　小时；

（2）求高速列车离乙地的路程与行驶时间之间的函数关系式，并写出的取值范围．

六、（本题满分12分）

21．（12分）设一次函数是常数，且．

（1）若函数的图象经过点，求函数的表达式．

（2）已知点，和在函数的图象上，若，求的取值范围．

（3）若一次函数的图象与的图象始终经过同一定点，探究实数，满足的关系式．

七、（本题满分12分）

22．（12分）如图，已知直线经过点，与轴交于点，与直线交于点．

（1）求直线的函数表达式及的值；

（2）根据函数图象，直接写出关于的不等式组的解集：　　；

（3）现有一点在直线上，过点作轴交直线于点，若点到线段的距离为1，求点的坐标和点的坐标．

八、（本题满分14分）

23．（14分）为鼓励群众积极参与全民健身，某游泳馆面向社会推出优惠活动，活动套餐如下：

优惠套餐一：购买一张会员卡，每次游泳按五折消费；

优惠套餐二：不购买会员卡，每次游泳按七五折消费．

若在此优惠活动期间来此游泳馆游泳（次，按套餐一所需费用为（元，且；

按套餐二所需费用为（元，且，其函数图象如图所示．

（1）求和的值，并说明它们表示的实际意义；

（2）求优惠活动前每次游泳的费用和的值；

（3）小明在优惠活动期间来此游泳馆游泳，请你通过计算说明他应该如何选择套餐更省钱．

2022-2023学年安徽省滁州市定远一中八年级（上）第一次月考数学试卷

参考答案与试题解析

一、选择题（本大题共10小题，每小题4分，满分40分，每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的）

1．（4分）在平面直角坐标系中，点的坐标为，则点在　　

A．第一象限 B．第二象限 C．第三象限 D．第四象限

【分析】直接利用第四象限内的点：横坐标大于0，纵坐标小于0，即可得出答案．

【解答】解：点的横坐标大于0，纵坐标小于0，

点在第四象限．

故选：．

2．（4分）在函数中，自变量的取值范围是　　

A． B． C． D．

【分析】根据二次根式可得，然后进行计算即可解答．

【解答】解：由题意得：

，

解得：；

故选：．

3．（4分）球的体积是，球的半径为，则，其中变量和常量分别是　　

A．变量是，；常量是， B．变量是，；常量是 

C．变量是，，；常量是 D．变量是，；常量是

【分析】根据常量和变量的概念解答即可．

【解答】解：球的体积是，球的半径为，则，

其中变量是，；常量是，

故选：．

4．（4分）已知函数是关于的正比例函数，则关于字母、的取值正确的是　　

A．， B．， C．， D．，

【分析】根据正比例函数的定义，列出式子即可解得答案．

【解答】解：是关于的正比例函数，

且，

，，

故选：．

5．（4分）如图，象棋盘上，若“将”位于点，“车”位于点，则“马”位于　　

A． B． C． D．

【分析】直接利用已知点坐标确定平面直角坐标系，进而得出答案．

【解答】解：如图所示：“马”位于．

故选：．

6．（4分）一次函数的图象如图所示，则关于的方程的解为　　

A． B． C． D．

【分析】通过图象与轴交点求解．

【解答】解：直线与轴交点坐标为，

的解为，

故选：．

7．（4分）八（1）班同学参加社会实践活动，在王伯伯的指导下，要围一个如图所示的长方形菜园，莱园的一边利用足够长的墙，用篱笆围成的另外三边的总长恰好为，设边的长为，边的长为．则与之间的函数表达式为　　

A． B． 

C． D．

【分析】根据菜园的三边的和为，即可得出一个与的关系式．

【解答】解：根据题意得，菜园三边长度的和为，

，

，

，，

，

解得，

，

故选：．

8．（4分）关于一次函数的图象，下列说法不正确的是　　

A．直线不经过第三象限 B．直线经过点 

C．直线与轴交于点 D．随的增大而增大

【分析】．利用一次函数图象与系数的关系，可得出一次函数的图象经过第一、二、四象限，即一次函数的图象不经过第三象限；

．利用一次函数图象上点的坐标特征，可得出一次函数的图象经过点；

．利用一次函数图象上点的坐标特征，可得出一次函数的图象与轴交于点；

．利用一次函数的性质，可得出随的增大而减小．

【解答】解：．，，

一次函数的图象经过第一、二、四象限，

即一次函数的图象不经过第三象限，选项不符合题意；

．当时，，

一次函数的图象经过点，选项不符合题意；

．当时，，

解得：，

一次函数的图象与轴交于点，选项不符合题意；

．，

随的增大而减小，选项符合题意．

故选：．

9．（4分）直线和在同一平面直角坐标系中的图象可能是　　

A． B． 

C． D．

【分析】先看一条直线，得出和的符号，然后再判断另外一条直线是否正确，这样可得出答案．

【解答】解：、直线中，，直线中，，、的取值相矛盾，故本选项不符合题意；

、直线中，，直线中，，、的取值一致，故本选项符合题意；

、直线中，，直线中，，、的取值相矛盾，故本选项不符合题意；

、直线中，，直线中，，、的取值相矛盾，故本选项不符合题意．

故选：．

10．（4分）如图，一次函数的图象与轴、轴分别相交于点，，若点在三角形的内部，则的取值范围是　　

A． B． C． D．

【分析】利用一次函数图象上点的坐标特征可得出点的坐标，结合点在三角形的内部，即可得出关于的一元一次不等式组，解之即可求出的取值范围．

【解答】解：当时，，

解得：，

点的坐标为．

点在三角形的内部，

，

解得：．

故选：．

二、填空题（本大题共4小题，每小题5分，满分20分）

11．（5分）点到轴的距离为4，到轴的距离为5，且点位于第三象限，则点的坐标为 　　．

【分析】根据平面直角坐标系中点到轴的距离等于纵坐标的绝对值，到轴的距离等于横坐标的绝对值，然后再根据第三象限内点的坐标特征，即可解答．

【解答】解：在平面直角坐标系的第三象限内有一点，到轴的距离为4，到轴的距离为5，则点的坐标为．

故答案为：．

12．（5分）点在函数的图象上，则代数式的值等于 　2022　．

【分析】利用一次函数图象上点的坐标特征，可得出，将其代入代数式中即可求出结论．

【解答】解：点在函数的图象上，

，

．

故答案为：2022．

13．（5分）如图，根据流程图中的程序，当输入数值为10时，输出数值为 　9　．

【分析】根据题意可得，因为，所以把代入中，计算即可得出答案．

【解答】解：根据题意可得，

，

把代入中，

得．

故答案为：9．

14．（5分）定义：在函数中，我们把关于的一次函数与称为一组对称函数，例如与是一组对称函数．请完成下列问题：

（1）一次函数的对称函数在轴上的截距为 　　；

（2）若一次函数的对称函数与轴交于点，与轴交于点，且三角形的面积为12，则的值为 　　．

【分析】（1）根据对称函数的定义，可知一次函数的对称函数，进一步求截距即可；

（2）根据对称函数的定义，可知一次函数的对称函数为，分别求出和点坐标，再根据三角形的面积为12，求出的值．

【解答】解：（1）根据对称函数的定义，

可知一次函数的对称函数是，

一次函数在轴上的截距为，

故答案为：；

（2）根据对称函数的定义，

可知一次函数的对称函数为，

当时，，

点坐标为，

，

，

当时，，

点坐标为，，

，

三角形的面积为12，

，

解得或（舍，

故答案为：12．

三、（本大题共2小题，每小题8分，满分16分）

15．（8分）已知与成正比例，且时，．求与之间的函数表达式．

【分析】根据正比例函数的定义，设，然后把已知的一组对应值代入求出，从而得到与之间的函数表达式．

【解答】解：设，

把，代入得，

解得，

，

与之间的函数表达式为．

16．（8分）如图，在平面直角坐标系中，三角形的顶点都在网格点上．

（1）将三角形向右平移5个单位长度，再向下平移4个单位长度得到三角形，请画出三角形；

（2）若三角形内有一点，平移后的三角形内的对应点为，直接写出点的坐标：　　．

【分析】（1）利用点平移的坐标变换规律得到、、的坐标，然后描点即可；

（2）利用（1）中点的坐标变换规律求解．

【解答】解；（1）如图，三角形为所作；

（2）点的坐标为．

故答案为：．

四、（本大题共2小题，每小题8分，满分16分）

17．（8分）已知是的一次函数，且当时，；当时，．

（1）求这个一次函数的表达式；

（2）当时，直接写出函数的取值范围，

【分析】（1）利用待定系数法求一次函数解析式；

（2）分别计算出自变量为和2所对应的函数值，然后根据一次函数的性质求解．

【解答】解：（1）设这个一次函数的表达式为，

根据题意得，

解得，

这个一次函数的表达式为；

（2）当时，；

当时，，

当时，对应的函数的取值范围为．

18．（8分）在平面直角坐标系中，点从原点出发，沿轴正方向按折线不断向前运动，其移动路线如图所示．这时点，，，的坐标分别为，，，，，按照这个规律，解决下列问题：

（1）写出下列点的坐标：　　，　　，　　，　　；

（2）点和点的位置分别在 　　，　　．（填轴上方、轴下方或轴上）

【分析】（1）根据图象可得点，，，的坐标；

（2）根据图象可得移动6次图象完成一个循环，从而可得出点和点的坐标．

【解答】解：（1）根据题意可知，，，，，，，，；

（2）根据图象可得移动6次图象完成一个循环，

，，

则点的纵坐标是0，点的纵坐标是，

点在轴上，在轴下方．

故答案为：轴上，轴下方．

五、（本大题共2小题；每小题10分，满分20分）

19．（10分）在平面直角坐标系中，已知点，试分别根据下列条件，求出点的坐标．

（1）点的纵坐标比横坐标小2．

（2）点到两坐标轴的距离相等．

【分析】（1）根据题意可得，进行计算即可解答；

（2）根据题意可得：或，然后分别进行计算即可解答．

【解答】解：（1）由题意得：

，

解得：，

当时，，，

点的坐标为；

（2）根据题意可得：

或，

或，

当时，，，

则点的坐标为；

当时，，，

则点的坐标为，；

综上所述：点的坐标为或，．

20．（10分）如图1所示，某乘客乘高速列车从甲地经过乙地到丙地，假设列车匀速行驶．如图2所示的是列车离乙地路程（千米）与列车从甲地出发后行驶时间（时之间的函数关系图象．

（1）甲、丙两地间的路程为 　1050　千米，从甲地到丙地共用 　　小时；

（2）求高速列车离乙地的路程与行驶时间之间的函数关系式，并写出的取值范围．

【分析】（1）由图可知，甲地到乙地距离，用时3小时，可得列车速度，乙地与丙地距离，进而得到甲、丙间的距离；

（2）先求出列车到达丙地的时间，然后用待定系数法分别求出从甲到乙、从乙到丙时，与的函数关系式；

【解答】解：（1）由函数图象可知，当时，

甲与乙的距离为900千米，

当时，表示3小时后列车到达乙地，

列车速度为：（千米小时），

（小时），

到达乙地后0.5小时列车到达丙地，乙与丙间的距离为150千米，

甲、丙两地间的路程为1050千米，从甲地到丙地共用3.5小时，

故答案为：1050，3.5；

（2）当时，设函数关系式为：，

将，代入得：

，

解得：，

；

当时，设函数关系式为：，

将，代入得：

，

解得：，

；

．

六、（本题满分12分）

21．（12分）设一次函数是常数，且．

（1）若函数的图象经过点，求函数的表达式．

（2）已知点，和在函数的图象上，若，求的取值范围．

（3）若一次函数的图象与的图象始终经过同一定点，探究实数，满足的关系式．

【分析】（1）根据待定系数法，可得函数解析式；

（2）根据一次函数的性质，可得答案；

（3）根据函数图象上的点满足函数解析式，可得答案．

【解答】解：（1）函数的图象经过点，

，

解得，

函数的表达式；

（2）当时，若，则；

当时，若，则；

（3），

函数的图象经过定点，

当经过时，，即．

七、（本题满分12分）

22．（12分）如图，已知直线经过点，与轴交于点，与直线交于点．

（1）求直线的函数表达式及的值；

（2）根据函数图象，直接写出关于的不等式组的解集：　　；

（3）现有一点在直线上，过点作轴交直线于点，若点到线段的距离为1，求点的坐标和点的坐标．

【分析】（1）通过待定系数法求出直线解析式，将点坐标代入求出的值．

（2）根据点，坐标结合图象求解．

（3）由点到线段的距离为1，可得点，的横坐标，通过分类讨论求解．

【解答】解：（1）将，代入得，

解得，

．

将代入得．

（2）点坐标为，点坐标为，

由图象得时，，

故答案为：．

（3）点到线段的距离为1，点横坐标为3，

点，横坐标为或，

将代入得，

点坐标为，

将代入得，

点坐标为，

将代入得，

点坐标为，

将代入得，

点坐标为，

综上所述，点，坐标为，或，．

八、（本题满分14分）

23．（14分）为鼓励群众积极参与全民健身，某游泳馆面向社会推出优惠活动，活动套餐如下：

优惠套餐一：购买一张会员卡，每次游泳按五折消费；

优惠套餐二：不购买会员卡，每次游泳按七五折消费．

若在此优惠活动期间来此游泳馆游泳（次，按套餐一所需费用为（元，且；

按套餐二所需费用为（元，且，其函数图象如图所示．

（1）求和的值，并说明它们表示的实际意义；

（2）求优惠活动前每次游泳的费用和的值；

（3）小明在优惠活动期间来此游泳馆游泳，请你通过计算说明他应该如何选择套餐更省钱．

【分析】（1）把点，代入，得到关于和的二元一次方程组，求解即可；

（2）根据套餐一每次游泳费用按五折优惠，可得打折前的每次游泳费用，再根据套餐二每次游泳费用按七五折优惠，求出的值；

（3）分三种情况列方程或不等式可解得答案．

【解答】解：（1）的图象过点，，

，

解得，

表示的实际意义是：购买一张会员卡后每次游泳费用为16元，

表示的实际意义是：购买一张会员卡的费用为40元；

（2）由题意可得，优惠活动前每次游泳的费用为（元，

；

（3）由题意可知，，．

，

解得：，

游泳5次时，套餐一，套餐二费用相同，

由，

解得：，

游泳小于5次时，选择套餐二所需费用少，

由，

解得：，

游泳大于5次时，选择套餐一所需费用少，

综上所述，游泳5次时，套餐一，套餐二费用相同，游泳小于5次时，选择套餐二所需费用少，游泳大于5次时，选择套餐一所需费用少．