苏教版 (2019)选择性必修第一册4.3 等比数列习题课件ppt

这是一份苏教版 (2019)选择性必修第一册4.3 等比数列习题课件ppt，共60页。PPT课件主要包含了并项求和，反思感悟，错位相减法，随堂演练，课时对点练，n－12n＋1等内容，欢迎下载使用。

1.熟练掌握等差与等比数列前n项和公式中各个符号的意义.
2.根据数列的结构形式会用并项法和错位相减法求和.
已知数列an＝(－1)nn，求数列{an}的前n项和Sn.
方法二　可采用分组求和(略).
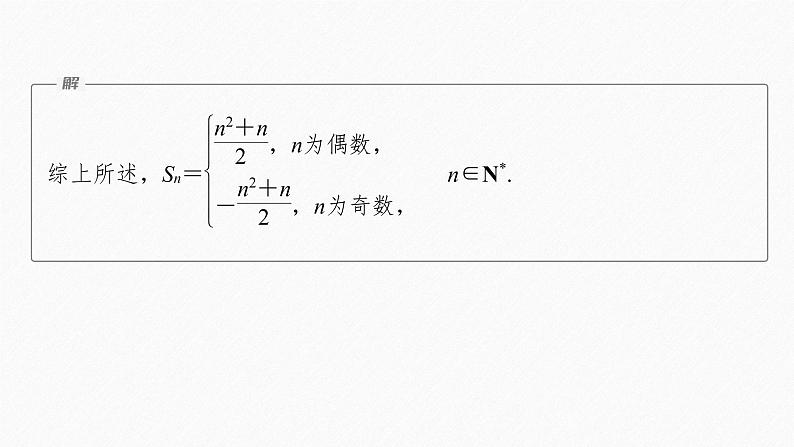
延伸探究　若an＝(－1)nn2，求数列{an}的前n项和Sn.
并项求和法适用的题型一般地，对于摆动数列适用于并项求和，此类问题需要对项数的奇偶性进行分类讨论，有些摆动型的数列也可采用分组求和.
若数列{an}的通项公式是an＝(－1)n＋1·(3n－2)，则a1＋a2＋…＋a2 023等于A.－3 027 B.3 027 C.－3 034 D.3 034
S2 023＝(1－4)＋(7－10)＋…＋(6 061－6 064)＋6 067＝1 011×(－3)＋6 067＝3 034.
求和：Sn＝x＋2x2＋3x3＋…＋nxn(x≠0).
当x≠1时，Sn＝x＋2x2＋3x3＋…＋nxn，xSn＝x2＋2x3＋3x4＋…＋(n－1)xn＋nxn＋1，
(1)一般地，如果数列{an}是等差数列，{bn}是等比数列，求数列{an·bn}的前n项和时，可采用错位相减法.(2)用错位相减法求和时，应注意：①要善于识别题目类型，特别是等比数列的公比为负数的情形.②在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”，以便于下一步准确地写出“Sn－qSn”的表达式.
可得Sn＝n(a1＋n－1)，∴a1＋a2＝2(a1＋1)，且a2＝3.解得a1＝1.∴Sn＝n2.∴n≥2时，an＝Sn－Sn－1＝n2－(n－1)2＝2n－1(n＝1时也成立).∴an＝2n－1.
(2)设bn＝an·3n，求数列{bn}的前n项和Tn.
bn＝an·3n＝(2n－1)·3n，∴数列{bn}的前n项和Tn＝3＋3×32＋5×33＋…＋(2n－1)×3n，∴3Tn＝32＋3×33＋…＋(2n－3)×3n＋(2n－1)×3n＋1，
可得Tn＝3＋(n－1)×3n＋1.
1.知识清单： (1)并项求和. (2)错位相减法求和.2.方法归纳：公式法、错位相减法.3.常见误区：并项求和易忽略总项数的奇偶；错位相减法中要注意相减后的项数、符号及化简.
1.已知在前n项和为Sn的数列{an}中，a1＝1，an＋1＝－an－2，则S101等于A.－97 B.－98 C.－99 D.－100
由an＋1＝－an－2，得an＋an＋1＝－2，则S101＝a1＋(a2＋a3)＋…＋(a100＋a101)＝1－2×50＝－99.
3.化简Sn＝n＋(n－1)×2＋…＋2×2n－2＋2n－1的结果是A.2n＋1＋n－2 B.2n＋1－n＋2C.2n－n－2 D.2n＋1－n－2
Sn＝n＋(n－1)×2＋(n－2)×22＋…＋2×2n－2＋2n－1，①2Sn＝n×2＋(n－1)×22＋(n－2)×23＋…＋2×2n－1＋2n，②②－①得：
1.若数列{an}的通项公式是an＝(－1)n(3n－1)，则a1＋a2＋…＋a10等于A.15 B.12 C.－12 D.－15
因为an＝(－1)n(3n－1)，所以a1＋a2＝－2＋5＝3，a3＋a4＝－8＋11＝3，a5＋a6＝－14＋17＝3，a7＋a8＝－20＋23＝3，a9＋a10＝－26＋29＝3，因此a1＋a2＋…＋a10＝3×5＝15.
2.已知数列{an}中，a1＝1，an＋an＋1＝3，Sn为其前n项和，则S2 023等于A.3 030 B.3 031 C.3 032 D.3 034
由题意a2＝2，a3＝1，a4＝2…，故奇数项为1，偶数项为2，则S2 023＝(a1＋a2)＋(a3＋a4)＋…＋(a2 021＋a2 022)＋a2 023＝3×1 011＋1＝3 034.
3.数列{an}满足a1＝1，a2＝3，且an＋1＋2an＋an－1＝0(n≥2)，则{an}的前2 022项和为A.8 088 B.4 044 C.－4 044 D.0
由递推关系式可得a1＋a2＝－(a2＋a3)，a2＋a3＝－(a3＋a4)，所以a3＋a4＝a1＋a2＝4，同理可得a5＋a6＝a7＋a8＝…＝a2 019＋a2 020＝a2 021＋a2 022＝4，所以S2 022＝4×1 011＝4 044.
∵an＝f(n)＋f(n＋1)
∴an＝(－1)n·(2n＋1)，∴an＋an＋1＝2(n是奇数)，∴a1＋a2＋a3＋…＋a100＝(a1＋a2)＋(a3＋a4)＋…＋(a99＋a100)＝2＋2＋2＋…＋2＝100.
5.已知公差不为零的等差数列{an}满足a1＝5，且a3，a6，a11成等比数列，设bn＝an×3n－1，则{bn}的前n项和Sn为A.n×3n－1 B.(n＋1)×3n－1C.(2n＋3)×3n－1－1 D.(2n＋1)×3n＋1
设{an}的公差为d，由a3，a6，a11成等比数列得
又a1＝5，可得d＝2，∴an＝2n＋3.∴bn＝(2n＋3)×3n－1，∴Sn＝5×30＋7×31＋9×32＋…＋(2n＋3)×3n－1，3Sn＝5×31＋7×32＋…＋(2n＋1)×3n－1＋(2n＋3)×3n，
∴Sn＝(n＋1)×3n－1.
6.(多选)已知数列{an}为等差数列，a1＝1，且a2，a4，a8是一个等比数列中的相邻三项，记bn＝an·2an，则{bn}的前n项和可以是A.n ＋1－2 D.(n－1)2n＋1＋2
∴an＝1或an＝1＋1×(n－1)＝n.当an＝1时，bn＝an· ＝2；当an＝n时，bn＝an· ＝n·2n.若bn＝2，则{bn}的前n项和为2n；若bn＝n·2n，设{bn}的前n项和为Sn，
则Sn＝1·21＋2·22＋3·23＋…＋n·2n，①∴2Sn＝1·22＋2·23＋3·24＋…＋n·2n＋1，②
所以S100＝a1＋a2＋a3＋a4＋a5＋a6＋…＋a97＋a98＋a99＋a100 ＝(a1＋a2＋a3)＋(a4＋a5＋a6)＋…＋(a97＋a98＋a99)＋a100＝a100＝a1＝1.
8.已知数列{an}的前n项和为Sn，且满足Sn＝2an－1(n∈N*)，则数列{nan}的前n项和Tn为______________.
∵Sn＝2an－1(n∈N*)，∴n＝1时，a1＝2a1－1，解得a1＝1，n≥2时，an＝Sn－Sn－1＝2an－1－(2an－1－1)，化为an＝2an－1，∴数列{an}是首项为1，公比为2的等比数列，∴an＝2n－1.又n＝1时，满足上式.∴nan＝n·2n－1.则数列{nan}的前n项和Tn＝1＋2×2＋3×22＋…＋n·2n－1.∴2Tn＝2＋2×22＋…＋(n－1)×2n－1＋n·2n，
∴Tn＝(n－1)2n＋1.
9.已知等差数列{an}的前n项和为Sn，且满足a3＝8，S5＝2a7.(1)求数列{an}的通项公式；
所以an＝a1＋(n－1)d＝2＋3(n－1)＝3n－1.
(2)若数列{bn}满足bn＝ancs nπ＋2n＋1，求数列{bn}的前2n项和T2n.
bn＝ancs nπ＋2n＋1＝(－1)nan＋2n＋1，T2n＝(a2－a1)＋(a4－a3)＋…＋(a2n－a2n－1)＋(22＋23＋…＋22n＋1)
10.已知{an}是各项均为正数的等比数列，且a1＋a2＝6，a1a2＝a3.(1)求数列{an}的通项公式；
设数列{an}的公比为q，
又an>0，解得a1＝2，q＝2，所以an＝2n.
又S2n＋1＝bnbn＋1，bn＋1≠0，所以bn＝2n＋1.
11.已知{an}的前n项和为Sn，a1＝1，当n≥2时，an＋2Sn－1＝n，则S2 023的值为A.1 008 B.1 009 C.1 010 D.1 012
由题意，当n≥2时，可得Sn－1＝Sn－an，因为an＋2Sn－1＝n，所以an＋2(Sn－an)＝n，即2Sn＝an＋n，当n≥3时，2Sn－1＝an－1＋n－1，两式相减，可得2an＝an－an－1＋1，即an＋an－1＝1，所以a2＋a3＝1，a4＋a5＝1，a6＋a7＝1，…，所以S2 023＝a1＋(a2＋a3)＋(a4＋a5)＋…＋(a2 022＋a2 023)＝1＋1 011＝1 012.
12.公元1202年列昂那多·斐波那契(意大利著名数学家)以兔子繁殖为例，引入“兔子数列”{an}：1,1,2,3,5,8,13,21,34,55，…，即a1＝1，a2＝1，an＝an－1＋an－2(n∈N*，n>2)，此数列在现代物理、化学等学科都有着十分广泛的应用.若此数列{an}的各项除以2后的余数构成一个新数列{bn}，设数列{bn}的前n项的和为Tn，若数列{an}满足：cn＝a －anan＋2，设数列{cn}的前n项的和为Sn，则T2 022＋S2 022等于A.1 349 B.1 348 C.674 D.673
∵ “兔子数列”的各项为1,1,2,3,5,8,13,21,34,55，…，∴此数列被2除后的余数依次为：1,1,0,1,1,0,1,1,0，…，即b1＝1，b2＝1，b3＝0，b4＝1，b5＝1，b6＝0，…，∴数列{bn}是以3为周期的周期数列，∴T2 022＝674(b1＋b2＋b3)＝674×2＝1 348，
所以cn＝(－1)n，所以S2 022＝(－1＋1)＋(－1＋1)＋…＋(－1＋1)＝0.则T2 022＋S2 022＝1 348.
13.在数列{an}中，a1＝1，对于任意自然数n，都有an＋1＝an＋n·2n，则a15等于A.14·215＋2 B.13·214＋2C.14·215＋3 D.13·215＋3
an＋1－an＝n·2n，∴a2－a1＝1·21，a3－a2＝2·22，a4－a3＝3·23… an－an－1＝(n－1)·2n－1，以上n－1个等式，累加得an－a1＝1·21＋2·22＋3·23＋…＋(n－1)·2n－1， ①又∵2an－2a1＝1·22＋2·23＋3·24＋…＋(n－2)·2n－1＋(n－1)·2n， ②
①－ ②得a1－an＝2＋22＋23＋…＋2n－1－(n－1)·2n
∴an＝(n－2)·2n＋3(n≥2)，∴a15＝(15－2)·215＋3＝13·215＋3.
14.设Xn＝{1,2,3，…，n}(n∈N*)，对Xn的任意非空子集A，定义f(A)为A中的最大元素，当A取遍Xn的所有非空子集时，对应的f(A)的和为Sn，则S5＝________.
由Xn＝{1,2,3，…，n}(n∈N*)，Xn的任意非空子集A共有2n－1个，其中最大值为n的有2n－1，最大值为n－1的有2n－2个，…，最大值为1的有20＝1个，故Sn＝20×1＋21×2＋…＋2n－2×(n－1)＋2n－1×n，所以2Sn＝21×1＋22×2＋…＋2n－1×(n－1)＋2n×n，两式相减得－Sn＝1＋21＋22＋…＋2n－1－2n×n，
故Sn＝(n－1)·2n＋1，所以S5＝(5－1)×25＋1＝129.
15.在数列{an}中，a1＝1，a2＝2，且an＋2－an＝1＋(－1)n(n∈N*)，则a1＋a2＋…＋a51＝________.
当n为偶数时，an＋2－an＝2，
当n为奇数时，an＋2－an＝0，an＝1；
16.已知数列{an}满足a1＝1，an＋1＝2an＋λ(λ为常数).(1)试探究数列{an＋λ}是不是等比数列，并求an；
因为an＋1＝2an＋λ，所以an＋1＋λ＝2(an＋λ).又a1＝1，所以当λ＝－1时，a1＋λ＝0，数列{an＋λ}不是等比数列，此时an＋λ＝an－1＝0，即an＝1；当λ≠－1时，a1＋λ≠0，所以an＋λ≠0，所以数列{an＋λ}是以1＋λ为首项，2为公比的等比数列，此时an＋λ＝(1＋λ)2n－1，即an＝(1＋λ)2n－1－λ.
(2)当λ＝1时，求数列{n(an＋λ)}的前n项和Tn.