人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数课堂教学课件ppt

这是一份人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数课堂教学课件ppt，共29页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，请完成对应习题等内容，欢迎下载使用。

1.会用配方法或公式法将一般式 y＝ax2＋bx＋c 化成顶点式 y=a(x-h)2+k. （难点） 2.会熟练求出二次函数一般式 y＝ax2＋bx＋c 的顶点坐标、对称轴. （重点）
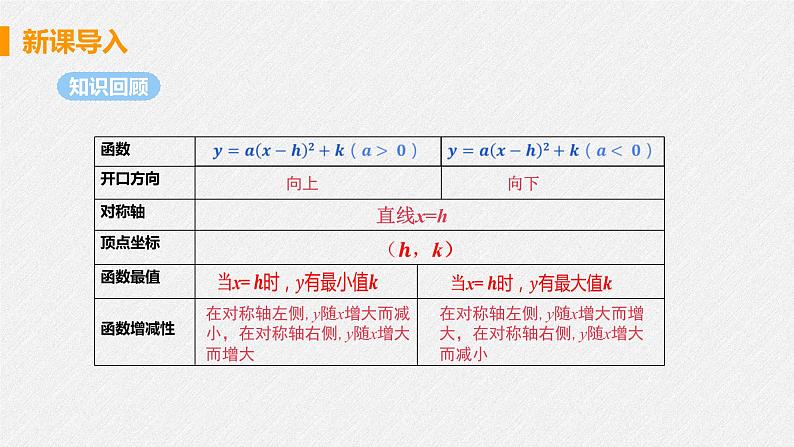
在对称轴左侧,y随x增大而减小，在对称轴右侧,y随x增大而增大
在对称轴左侧,y随x增大而增大，在对称轴右侧,y随x增大而减小
知识点1 二次函数y=ax2+bx+c的图像和性质
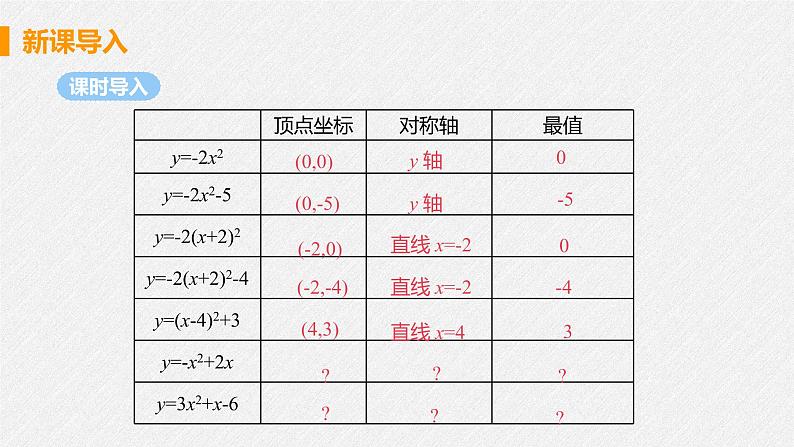
对称轴是直线 x=6，顶点坐标是(6，3).
平移方法 1： 先向上平移 3 个单位，再向右平移 6 个单位得到的；平移方法 2： 先向右平移 6 个单位，再向上平移 3 个单位得到的.
1.描点法：①用配方法把二次函数 y=ax2+bx+c 化成 y=a(x-h)2+k 的形式； ②确定抛物线的开口方向、对称轴和顶点坐标，在对称轴两侧 对称取点，按列表、描点、连线的步骤画出抛物线.
画二次函数 y=ax2+bx+c 的图象的方法
2.平移法：①用配方法把二次函数 y=ax2+bx+c 化成 y=a(x-h)2+k 的形式， 明确顶点 (h，k)； ②作出抛物线 y=ax2； ③将抛物线 y=ax2 平移，使其顶点平移到 (h，k) 处.
先利用图形的对称性列表.
然后描点画图，得到图象如图.
当 x<6 时，y 随 x 的增大而减小；当 x>6 时，y 随 x 的增大而增大.
知识点2 将一般式 y=ax2+bx+c(a≠0) 化成顶点式 y=a(x-h)2+k
y=ax²+bx+c
知识点3 二次函数y=ax2+bx+c的图象与a，b，c之间的关系
二次函数 的图象如下图所示，请根据二次函数的性质填空：
二次函数 y=ax2+bx+c 的图象与 a，b，c 的关系
二次函数 y=ax2+bx+c 中，a 的符号决定抛物线的开口方向，a，b 的符号决定抛物线的对称轴的大致位置，c 的符号决定抛物线与 y 轴交点的大致位置.
A.1B.2C.3D.4
2二次函数 y=ax2+bx+c 图象如图所示，下列结论：①b<0；②c>0；③a+b+c>0；④4a+2b+c<0.其中正确的个数是( )
解：①因为二次函数 y=ax2+bx+c 的图象的开口方向是向下，所以 a＜0，根据对称轴在 y 轴的右侧，所以a，b的符号相反，得出b＞0，故①错误；②因为二次函数 y=ax2+bx+c的图象与y轴正半轴相交，所以c＞0，故②正确；③根据图象知，当x=1时，y＞0，即a+b+c＞0，故③正确；④根据图象知，当x=2时，y < 0，∴4a+2b+c<0，故④正确；综上所述，正确结论共3个，故选C．
y=ax2+bx+c（a ≠0)(一般式)
二次函数 y=ax2+bx+c 的图象与性质：
1.李玲用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格，根据表格上的信息回答问题：该二次函数y=ax2+bx+c，当x=3时，y= ．
2.确定下列抛物线的开口方向、对称轴及顶点坐标.（1）y=2x2+8x－6； （2）y=12x2－48x+45. 
开口向上，对称轴为x=-2顶点为（-2，-14）.
开口向上，对称轴为x=2，顶点为（2，-3）.
3.从地面向上抛出一个小球，小球的高度h(单位：m)与小球的运动时间t(单位：s)之间的关系式是h=30t-5t2.小球运动到最高点时，所花时间是多少？最高点的高度是多少？
解：小球在顶点时达到最大高度.∴所花时间是3s，最高点的高度是45m.
A.①②③B.②③⑤C.②③④D.③④⑤
已知二次函数 y=ax2+bx+c(a≠0) 的图象如图所示，有下列 5 个结论：①abc>0；②b-a>c；③4a+2b+c>0；④3a>-c；⑤a+b>m(am+b)(m≠1).其中正确的结论有( )