重庆市南岸区3年（2020-2022）九年级数学上学期期末试题汇编-02填空题

重庆市南岸区3年（2020-2022）九年级数学上学期期末试题汇编-02填空题

1．（2022·重庆南岸·九年级期末）方程的两个根为___________．

2．（2022·重庆南岸·九年级期末）如图，晚上小亮在路灯下散步，在由A点处走到B点处这一过程中，他在点A，B，C三处对应的在地上的影子，其中影子最短的是在 _____点处（填A，B，C）．

3．（2022·重庆南岸·九年级期末）若∠A是锐角，且cosA＝，则sinA＝_____．

4．（2022·重庆南岸·九年级期末）若，则=______.

5．（2022·重庆南岸·九年级期末）如图，院子里有块直角三角形空地ABC，∠C＝90°．直角边AC＝3m、BC＝4m，现准备修一个如图所示的矩形DEFG的养鱼池，当矩形DEFG面积最大时，EF的长为 _____．

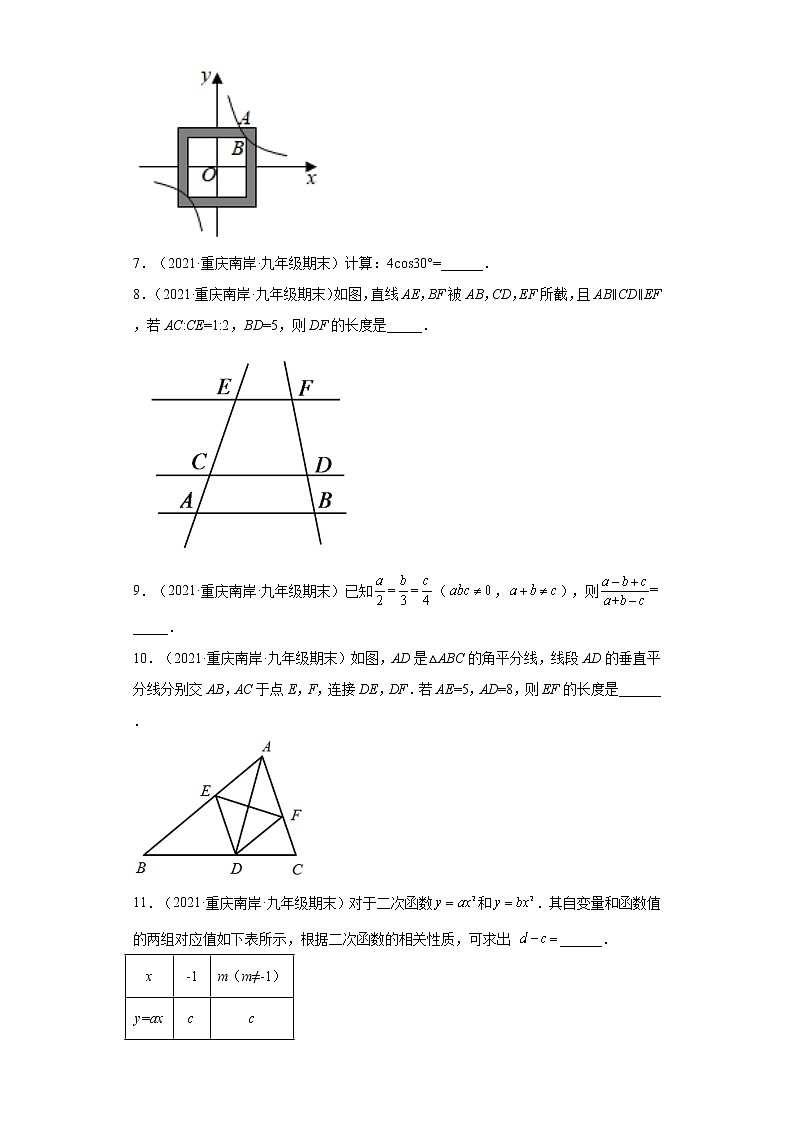
6．（2022·重庆南岸·九年级期末）如图，大、小两个正方形的中心均与平面直角坐标系的原点O重合，边分别与坐标轴平行．反比例函数y＝（k≠0）的图象，与大正方形的一边交于点A（，4），且经过小正方形的顶点B．求图中阴影部分的面积为 _____．

7．（2021·重庆南岸·九年级期末）计算：4cos30°=______．

8．（2021·重庆南岸·九年级期末）如图，直线AE，BF被AB，CD，EF所截，且AB∥CD∥EF，若AC:CE=1:2，BD=5，则DF的长度是_____．

9．（2021·重庆南岸·九年级期末）已知（，），则_____．

10．（2021·重庆南岸·九年级期末）如图，AD是△ABC的角平分线，线段AD的垂直平分线分别交AB，AC于点E，F，连接DE，DF．若AE=5，AD=8，则EF的长度是______．

11．（2021·重庆南岸·九年级期末）对于二次函数和．其自变量和函数值的两组对应值如下表所示，根据二次函数的相关性质，可求出 ______．

12．（2021·重庆南岸·九年级期末）如图，在正方形ABCD中，AB=，E是CD上一点，BE交AC于点F，连接DF．过点D且垂直于DF的直线，与过点A且垂直于AC的直线交于点G．∠ABE 的平分线交AD于点M，当满足四边形面积时，线段AM的长度是_______．

13．（2020·重庆南岸·九年级期末）一元二次方程的根是_____．

14．（2020·重庆南岸·九年级期末）抛物线y＝（x+2）2+1的顶点坐标为_____．

15．（2020·重庆南岸·九年级期末）如图，有一斜坡，坡顶离地面的高度为，斜坡的倾斜角是，若，则此斜坡的为____m．

16．（2020·重庆南岸·九年级期末）如图，某校教学楼AC与实验楼BD的水平间距CD＝30m，在教学楼AC的底部C点测实验楼顶部B点的仰角为α，且sinα＝，在实验楼顶部B点测得教学楼顶部A点的仰角是30°，则教学楼AC的高度是_____m（结果保留根号）．

17．（2020·重庆南岸·九年级期末）如图，在直角坐标系中，正方形ABCD的边BC在x轴上，其中点A的坐标为（1，2），正方形EFGH的边FG在x轴上，且H的坐标为（9，4），则正方形ABCD与正方形EFGH的位似中心的坐标是_____．

参考答案：

1．，

【分析】方程利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．

【详解】方程（x＋2）（x−3）＝0，

可得x＋2＝0或x−3＝0，

解得：x1＝−2，x2＝3．

故答案为：x1＝−2，x2＝3．

【点睛】此题考查了解一元二次方程−因式分解法，熟练掌握因式分解法是解本题的关键．

2．C

【分析】如图所示，、 、分别为点A，B，C三处对应的在地上的影子，通过三角形相似，比较长度的大小，进而求得影子最短的值的点．

【详解】解：如图、、分别为点A，B，C三处对应的在地上的影子

由三角形相似可得

，

值最小

值最小

由题意可知，离路灯越近，影子越短

故答案为：C．

【点睛】本题考查了相似三角形．解题的关键是建立比较长度的关系式．

3．##0.8

【分析】根据cosA=，设出关于两边的代数表达式，再根据勾股定理求出第三边长的表达式即可推出sinA的值．

【详解】解：如图，在中，cosA＝=，

设，则

故答案为：．

【点睛】此题考查了同角三角函数的知识，求锐角的三角函数值的方法：利用锐角三角函数的定义，通过设参数的方法求三角函数值，或者利用同角（或余角）的三角函数关系式求三角函数值．

4．

【分析】根据比例的等比性质代入即可得解．

【详解】∵=，b+d≠0，∴=．

故答案为．

【点睛】本题考查了比例的等比性质，若a：b＝c：d＝…＝m：n，则（a+c+…+m）：（b+d+…+n）＝m：n（注意分母的和不为0），难度适中．

5．##

【分析】过点作，交于点，等面积法求得，设，进而根据得出比例式，根据矩形的面积为，得到关于的二次函数，根据二次函数的性质即可求得面积最大时的的值，进而求得的长．

【详解】解：如图，过点作，交于点，

∠C＝90°．直角边AC＝3m、BC＝4m，

设，则

四边形是矩形

，

整理得

设矩形的面积为，则

当取得最大值时，，此时

故答案为：

【点睛】本题考查了矩形的性质，勾股定理，相似三角形的性质与判定，二次函数的性质，掌握以上知识是解题的关键．

6．40

【分析】根据待定系数法求出即可得到反比例函数的解析式；利用反比例函数系数的几何意义求出小正方形的面积，再求出大正方形在第一象限的顶点坐标，得到大正方形的面积，根据图中阴影部分的面积大正方形的面积小正方形的面积即可求出结果．

【详解】解：反比例函数的图象经过点，

，

反比例函数的解析式为；

小正方形的中心与平面直角坐标系的原点重合，边分别与坐标轴平行，

设点的坐标为，

反比例函数的图象经过点，

，

，

小正方形的面积为，

大正方形的中心与平面直角坐标系的原点重合，边分别与坐标轴平行，且，

大正方形在第一象限的顶点坐标为，

大正方形的面积为，

图中阴影部分的面积大正方形的面积小正方形的面积．

【点睛】本题主要考查了待定系数法求反比例函数的解析式，反比例函数系数的几何意义，正方形的性质，熟练掌握反比例函数系数的几何意义是解决问题的关键．

7．

【分析】可利用30°特殊直角三角形三边关系并结合余弦三角函数定义求解本题．

【详解】30°直角三角形三边比例关系为，．

故4cos30°=．

故答案为：．

【点睛】本题考查余弦三角函数，熟练记忆其定义即可，对于特殊角度的三角形函数值，可背诵下来提升解题速度．

8．10

【分析】利用分线段成比例的性质计算即可．

【详解】∵AB∥CD∥EF，

∴，

∵BD=5，

∴，

∴．

故答案为：10．

【点睛】本题考查平行线分线段成比例性质，掌握平行线分线段成比例性质是解题关键．

9．3

【分析】设=k，用k表示出a、b、c的值，代入代数式计算化简即可．

【详解】设=k，则a=2k，b=3k，c=4k，

∴，

故答案为：3．

【点睛】此题考查分式的化简求值，设设=k，用k表示出a、b、c的值是解题的关键．

10．6

【分析】假设AD与EF相交于点H，由题意易得∠BAD=∠CAD，∠AHE=∠AHF=90°，进而可证△AHE≌△AHF，则有EH=HF，然后由勾股定理可求解．

【详解】解：假设AD与EF相交于点H，如图所示：

∵AD平分∠BAC，

∴∠BAD=∠CAD，

∵EF垂直平分AD，

∴AH=HD，∠AHE=∠AHF=90°，

∵AH=AH，

∴△AHE≌△AHF（ASA），

∴EH=FH，

∵AE=5，AD=8，

∴AH=4，

∴在Rt△AHE中，，

∴EF=6；

故答案为6．

【点睛】本题主要考查勾股定理及垂直平分线的性质定理，熟练掌握勾股定理及垂直平分线的性质定理是解题的关键．

11．3

【分析】根据二次函数的性质，可知m=1，代入，将d用含c的式子表示出来即可

【详解】解：由二次函数的性质可得的对称轴为y轴，

故由表可得

故答案为：3

【点睛】本题考查了二次函数的对称性，熟练掌握二次函数的性质是解题的关键

12．

【分析】根据正方形ABCD，得，，，结合题意推导得、，通过证明，得，从而得到正方形面积，结合四边形面积，计算得到；过点M作交BE于点N，连接ME，根据正方形ABCD，通过计算即可完成求解．

【详解】∵正方形ABCD

∴，，

∴，，

∵过点D且垂直于DF的直线，与过点A且垂直于AC的直线交于点G

∴，

∴，

∴，即

∴

∴

∴

∵四边形面积=正方形面积

∴四边形面积=

∵，且满足四边形面积

∴

∴

∴

如图，过点M作交BE于点N，连接ME

∵∠ABE 的平分线交AD于点M

∴

∵，

∴

∴，  

设

∵正方形ABCD

∴

∴

故答案为：．

【点睛】本题考查了正方形、全等三角形、一元一次方程、二次根式、三角形角平分线、勾股定理的知识；解题的关键是熟练掌握正方形、全等三角形、三角形角平分线的性质，从而完成求解．

13．

【分析】利用因式分解法把方程化为x-3=0或x-2=0，然后解两个一次方程即可．

【详解】解：或，

所以．

故答案为．

【点睛】本题考查了解一元二次方程-因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．

14．（﹣2，1）

【分析】根据题目中二次函数的顶点式可以直接写出它的顶点坐标．

【详解】由抛物线的顶点坐标可知，抛物线y＝（x+2）2+1的顶点坐标是（﹣2，1）．

故答案为：（﹣2，1）．

【点睛】本题考查二次函数的性质，解答本题的关键是由顶点式可以直接写出二次函数的顶点坐标．

15．75．

【分析】由三角函数定义即可得出答案．

【详解】解：∵， ，

∴；

故答案为：75．

【点睛】本题考查了解直角三角形的应用；熟练掌握三角函数定义是解题的关键．

16．（10+40）

【分析】首先分析图形，解直角三角形△BEC得出CE，再解直角三角形△ABE得出AE，进而即可求出答案．

【详解】解：过点B作BE⊥AB于点E，

在Rt△BEC中，∠CBE＝α，BE＝CD＝30；

可得CE＝BE×tanα，

∵sinα＝，

∴tanα＝，

∴CE＝30×＝40．

在Rt△ABE中，∠ABE＝30°，BE＝30，

可得AE＝BE×tan30°＝10．

故教学楼AC的高度是AC＝（10+40）m．

故答案为：（10+40）m．

【点睛】本题考查了解直角三角形-俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．

17．（﹣3，0）或（，）

【分析】连接HD并延长交x轴于点P，根据正方形的性质求出点D的坐标为（3，2），证明△PCD∽△PGH，根据相似三角形的性质求出OP，另一种情况，连接CE、DF交于点P，根据待定系数法分别求出直线DF解析式和直线CE解析式，求出两直线交点，得到答案．

【详解】解：连接HD并延长交x轴于点P，则点P为位似中心，

∵四边形ABCD为正方形，点A的坐标为（1，2），

∴点D的坐标为（3，2），

∵DC//HG，

∴△PCD∽△PGH，

∴，即，

解得，OP＝3，

∴正方形ABCD与正方形EFGH的位似中心的坐标是（﹣3，0），

连接CE、DF交于点P，

由题意得C（3，0），E（5，4），D（3，2），F（5，0），

求出直线DF解析式为：y＝﹣x+5，直线CE解析式为：y＝2x﹣6，

解得

直线DF，CE的交点P为（，），

所以正方形ABCD与正方形EFGH的位似中心的坐标是（，），

故答案为：（﹣3，0）或（，）．

【点睛】本题考查的是位似变换的概念和性质、相似三角形的判定和性质，位似图形的定义：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．