






初中数学人教版九年级上册24.1.1 圆课文内容ppt课件
展开1. 认识圆,理解圆的本质属性;(重点)2. 认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、 等弧等与圆有关的概念,并了解它们之间的区别和 联系;(难点)
观察下列生活中的图片,找一找你所熟悉的图形.
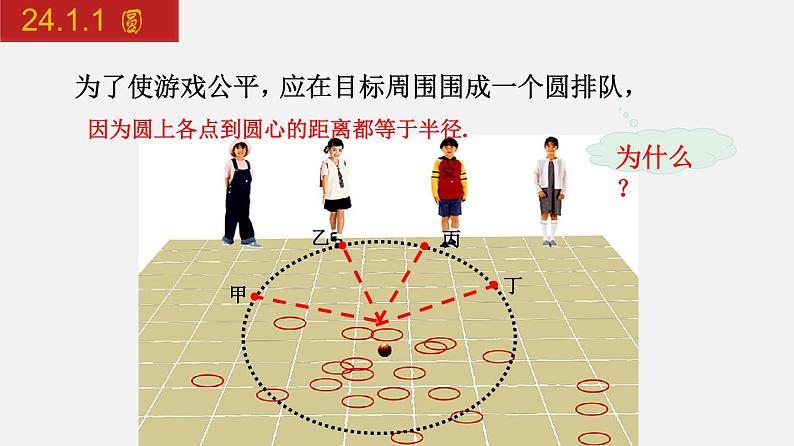
问题1 一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?
应在目标周围围成一个圆排队,
因为圆上各点到圆心的距离都等于半径.
问题2 观察画圆的过程,你能说出圆是如何画出来的吗?
如图,在平面内,线段 OP 绕它固定的一个端点 O 旋转一周,则另一个端点 P 所形成的封闭曲线叫做圆.
固定的端点 O 叫做圆心;
线段 OP 叫做半径;
以点 O 为圆心的圆,记作⊙O,读作“圆O”.
(1)确定一个圆需要两个要素,一是圆心,圆心确定其位置,二是半径,半径确定其大小.(2)圆是一条封闭的曲线,曲线是“圆周”,而 不能认为是“圆面”.(3)“圆上的点”指圆周上的点.
(1) 圆上各点到定点 (圆心O) 的距离都于 .(2) 平面内到定点 (圆心O) 的距离等于定长(半径r)的所有 点都在 .
由此,我们可以得到圆的集合定义:平面内到定点 (圆心O) 的距离等于定长(半径r)的所有点组成的图形.
想一想:从画圆的过程中,你能说出圆上的点有什么特性吗?
例1下列说法中,错误的有( )(1)经过点P的圆有无数个;(2)以点P为圆心的圆有无数个;(3)半径为3 cm且经过点P的圆有无数个;(4)以点P为圆心,3 cm为半径的圆有无数个. A.1个 B.2个 C.3个 D.4个
导引:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,由此可知(1)(2)正确;(3)半径确定,但圆心不确定,仍有无数个圆;(4)圆心和半径都确定的圆有且只有一个.
例2 矩形 ABCD 的对角线 AC、BD 相交于点 O.求证:A、B、C、D 在以 O 为圆心的同一圆上.
证明:∵ 四边形 ABCD 是矩形,
∴ AO = OC,OB = OD.
又∵ AC = BD,∴ OA = OB = OC = OD.
∴ A、B、C、D 在以 O 为圆心,以 OA 为半径的圆上.
连接圆上任意两点的线段(如图中的 AC)叫做弦.
经过圆心的弦(如图中的 AB)叫做直径.
探索:圆中最长的弦是什么?为什么?
【发现】直径是最长的弦
1. 根据圆的定义,“圆” 指的是 “圆周”,而不是 “圆面”;2. 直径是圆中最长的弦.
连接 OC.在△AOC 中,根据三角形三边关系有 AO + OC>AC,而 AB = 2OA,AO = OC,所以 AB>AC.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
小于半圆的弧叫做劣弧,如图中的 AC ;
大于半圆的弧叫做优弧,如图中的 ABC .
例3 如图.(1) 请写出以点 A 为端点的劣弧及优弧;(2) 请写出以点 A 为端点的弦及直径;
弦 AF,AB,AC. 其中弦 AB 也是直径.
(3) 请任选一条弦,写出这条弦所对的弧.
能够重合的两个圆叫做等圆.
容易看出: 等圆是两个半径相等的圆.
在同圆或等圆中,能够互相重合的弧叫做等弧.
结论:等弧仅仅存在于同圆或者等圆中.
可见这两条弧不可能完全重合
实际上这两条弧弯曲程度不同
相等“等弧”要区别于“长度的弧”
想一想:长度相等的弧是等弧吗?
∴∠ACD = 90° - 80° = 10°.
解:∵∠ACB = 90°,∠A = 40°,
∴∠BCD = 180° - 2×50° = 80°.
例5 以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧; (7)以O为圆心可以画无数个圆. 正确的个数为( ) A.1 B.2 C.3 D.4
要画一个确定的圆,关键是确定圆心和半径
1. 填空:(1)______是圆中最长的弦,它是______的 2 倍.(2)图中有 条直径, 条非直径的弦, 圆中以 A 为一个端点的优弧有 条,劣弧 有 条.
2. 判断下列说法的正误,并说明理由或举反例.
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
3.如图,点A,B,C在⊙O上,点O在线段AC上,点 D在线段AB上,下列说法正确的是( ) A.线段AB,AC,CD,OB都是弦 B.与线段OB相等的线段有OA,OC,CD C.图中的优弧有2条 D.AC是弦,AC又是⊙O的直径,所以弦是直径
4. 如图,AB 是⊙O 的直径,点 C、D 在⊙O 上,且点 C、D 在 AB 的异侧,连接 AD、OD、OC.若∠AOC = 70°,且 AD∥OC,求∠AOD 的度数.
解:∵AD∥OC,∴∠DAO =∠AOC = 70°.又∵OD = OA,∴∠ADO =∠DAO = 70°.∴∠AOD = 180-70°-70° = 40°.
初中数学第二十四章 圆24.1 圆的有关性质24.1.1 圆教学课件ppt: 这是一份初中数学第二十四章 圆24.1 圆的有关性质24.1.1 圆教学课件ppt,共35页。PPT课件主要包含了圆与圆的位置关系,dR+r,dR-r,d﹥6等内容,欢迎下载使用。
初中数学人教版九年级上册24.1.1 圆完美版课件ppt: 这是一份初中数学人教版九年级上册24.1.1 圆完美版课件ppt,共20页。PPT课件主要包含了图中都有圆,与圆有关的概念,同步练习,谈谈你有什么收获等内容,欢迎下载使用。
数学九年级上册24.1.1 圆习题课件ppt: 这是一份数学九年级上册24.1.1 圆习题课件ppt,共30页。PPT课件主要包含了任意两点,两点间的部分等内容,欢迎下载使用。













