高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线教学演示ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线教学演示ppt课件，文件包含321第2课时双曲线及其标准方程的应用pptx、321第2课时双曲线及其标准方程的应用docx等2份课件配套教学资源，其中PPT共60页， 欢迎下载使用。
1.会利用双曲线的定义和标准方程解决简单问题.
2.双曲线在实际生活中的应用.
双曲线是我们在平时生活中经常见到的图形，这节课研究双曲线在实际生活中的应用.
已知A(－4，0)，B是圆(x－1)2＋(y－4)2＝1上的点，点P在双曲线 ＝1的右支上，则|PA|＋|PB|的最小值为
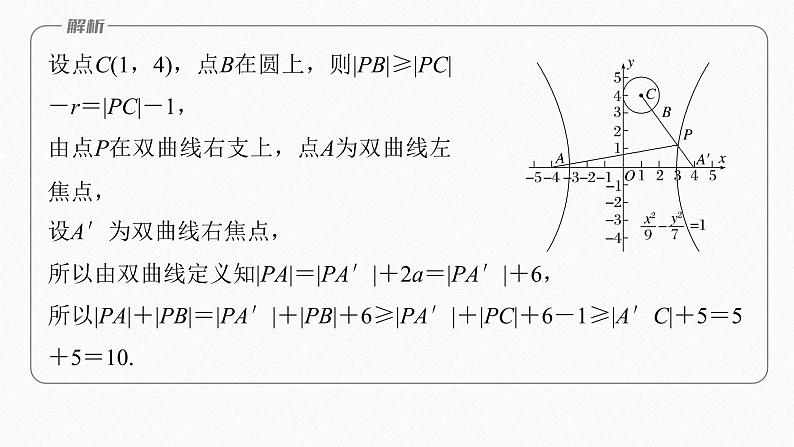
设点C(1，4)，点B在圆上，则|PB|≥|PC|－r＝|PC|－1，由点P在双曲线右支上，点A为双曲线左焦点，设A′为双曲线右焦点，
所以由双曲线定义知|PA|＝|PA′|＋2a＝|PA′|＋6，所以|PA|＋|PB|＝|PA′|＋|PB|＋6≥|PA′|＋|PC|＋6－1≥|A′C|＋5＝5＋5＝10.
求解与双曲线有关的长度和最值问题，都可以通过相应的双曲线的定义去解决.
设F1是双曲线的左焦点，根据双曲线的定义及P是双曲线右支上的动点可得|PF1|－|PF|＝2a，所以|PF|＝|PF1|－2a，所以|PA|＋|PF|＝|PA|＋|PF1|－2a＝|PA|＋|PF1|－4，
当且仅当P，A，F1三点共线时取得等号，即图形中点P在P′处取得最小值，
方法二　设双曲线的方程为my2－nx2＝1(mn>0)，
则MF1⊥MF2，设|MF1|＝m，|MF2|＝n，由双曲线定义，知m－n＝2a＝8，①又m2＋n2＝(2c)2＝80，②由①②得m·n＝8，
解得λ＝4或λ＝－14(舍去)，
(1)双曲线过两定点，可设其方程为mx2＋ny2＝1(mn0)，通过解方程组即可确定m，n，避免了讨论，实为一种好方法.
已知双曲线中，c＝ ，且经过点(－5，2)，焦点在x轴上，求该双曲线的标准方程.
∴λ＝5或λ＝30(舍去).
2021年9月17日神舟“十二号”返回舱顺利到达地球后，为了及时将航天员安全救出，地面指挥中心在返回舱预计到达区域安排了三个救援中心(记A，B，C)，A在B的正东方向，相距6千米，C在B的北偏西30°方向，相距4千米，P为航天员着陆点.某一时刻，A接收到P的求救信号，由于B，C两地比A距P远，在此4秒后，B，C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒，求在A处发现P的方位角.
如图所示，以直线AB为x轴，线段AB的垂直平分线为y轴建立平面直角坐标系，
∵|PB|＝|PC|，∴点P在线段BC的垂直平分线上，
又|PB|－|PA|＝4＜6＝|AB|，∴点P在以A，B为焦点的双曲线的右支上，
因此在A处发现P的方位角为北偏东30°.
利用双曲线解决实际问题的基本步骤(1)建立适当的坐标系.(2)求出双曲线的标准方程.(3)根据双曲线的方程及定义解决实际应用问题(注意实际意义).
如图，B地在A地的正东方向4 km处，C地在B地的北偏东30°方向2 km处，河流的沿岸PQ(曲线)上任意一点D到A的距离比到B的距离远
2 km，则曲线PQ的轨迹方程是________________；现要在曲线PQ上选一处M建一座码头，向B，C两地转运货物，那么这两条公路MB，MC的路程之和最短是__________km.
如图所示，以AB所在的直线为x轴，AB的垂直平分线为y轴建立平面直角坐标系.则A(－2，0)，B(2，0)，|DA|－|DB|＝2，根据双曲线定义知，轨迹为双曲线的右支.
当且仅当A，M，C三点共线时等号成立.
故2c＝4，c＝2，2a＝2，a＝1，b2＝c2－a2＝4－1＝3，
1.知识清单： (1)双曲线定义的应用. (2)双曲线方程的设法. (3)双曲线在实际生活中的应用.2.方法归纳：转化法.3.常见误区：双曲线在实际生活中的应用中，建模容易出错.
如图所示，设双曲线的右焦点为F2，连接P2F2，因为双曲线上的点P1与P2关于y轴对称，根据双曲线的对称性，可得|P1F1|＝|P2F2|，所以|P2F1|－|P1F1|＝|P2F1|－|P2F2|＝2×3＝6.
1.如图，双曲线C： ＝1的左焦点为F1，双曲线上的点P1与P2关于y轴对称，则|P2F1|－|P1F1|的值是A.3 B.4 C.6 D.8
由已知可得||PA|－|PB||＝2k