北师大版八年级上册3 勾股定理的应用课后作业题

这是一份北师大版八年级上册3 勾股定理的应用课后作业题，共14页。试卷主要包含了如图等内容，欢迎下载使用。
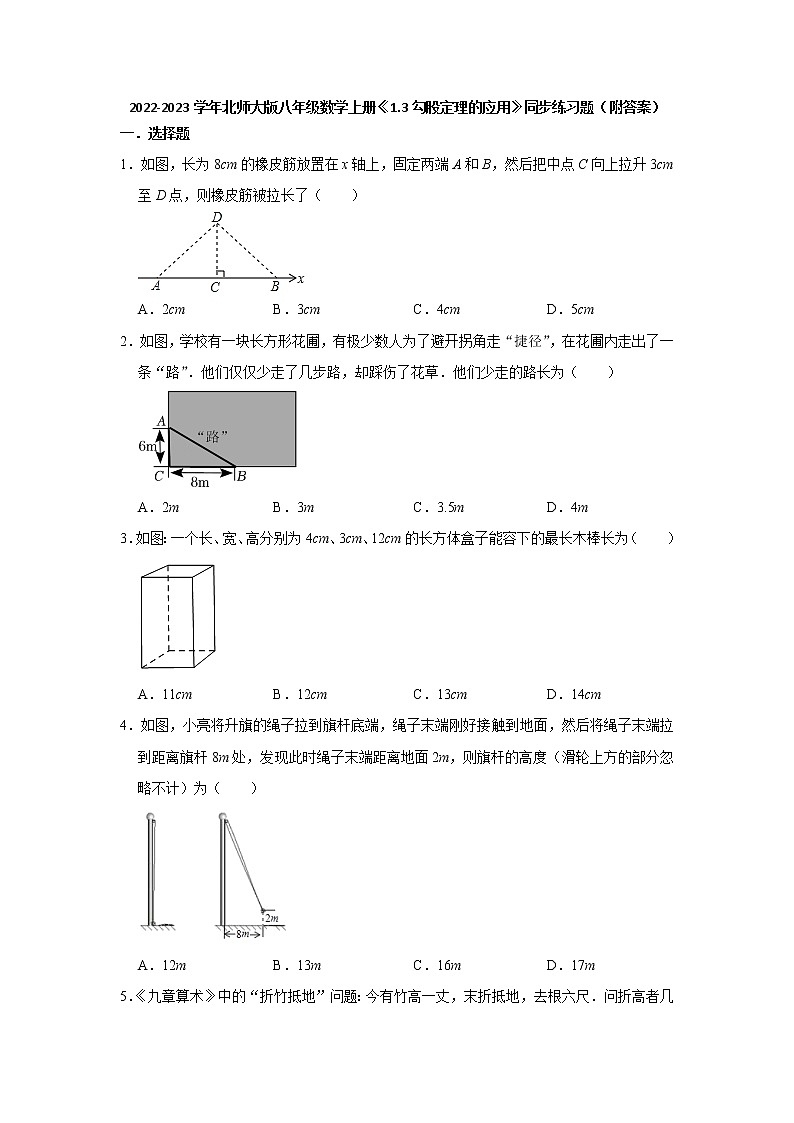
1．如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm至D点，则橡皮筋被拉长了（ ）
A．2cmB．3cmC．4cmD．5cm
2．如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了几步路，却踩伤了花草．他们少走的路长为（ ）
A．2mB．3mC．3.5mD．4m
3．如图：一个长、宽、高分别为4cm、3cm、12cm的长方体盒子能容下的最长木棒长为（ ）
A．11cmB．12cmC．13cmD．14cm
4．如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8m处，发现此时绳子末端距离地面2m，则旗杆的高度（滑轮上方的部分忽略不计）为（ ）
A．12mB．13mC．16mD．17m
5．《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺．问折高者几何？意思是：一根竹子，原高一丈（一丈＝10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，问折断处离地面的高度是多少？设折断处离地面的高度为x尺，则可列方程为（ ）
A．x2﹣6＝（10﹣x）2B．x2﹣62＝（10﹣x）2
C．x2+6＝（10﹣x）2D．x2+62＝（10﹣x）2
6．如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米．一只鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行（ ）
A．8米B．10米C．12米D．14米
7．如图，一个梯子AB长2.5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.5米，则梯子顶端A下落了（ ）米．
A．0.5B．1C．1.5D．2
8．如图，小明将一张长为20cm，宽为15cm的长方形纸（AE＞DE）剪去了一角，量得AB＝3cm，CD＝4cm，则剪去的直角三角形的斜边长为（ ）
A．5cmB．12cmC．16cmD．20cm
9．如图，在一个高为5m，长为13m的楼梯表面铺地毯，则地毯长度至少应是（ ）
A．13mB．17mC．18mD．25m
二．填空题
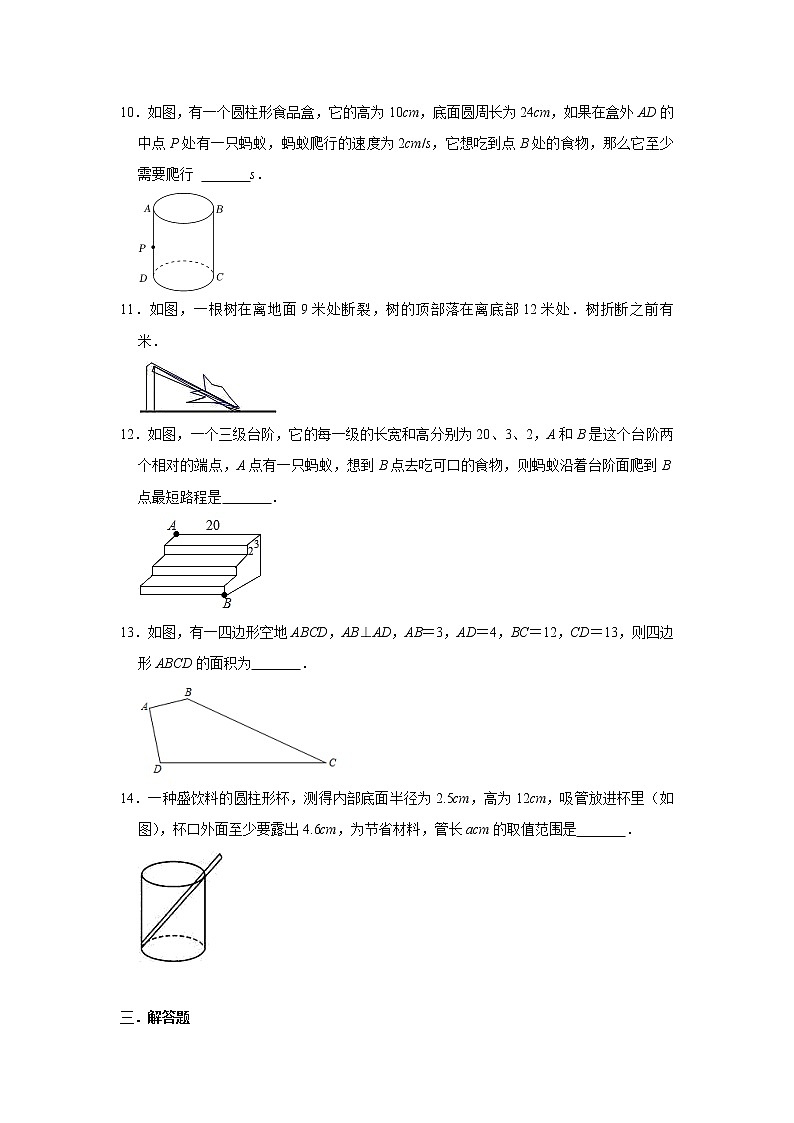
10．如图，有一个圆柱形食品盒，它的高为10cm，底面圆周长为24cm，如果在盒外AD的中点P处有一只蚂蚁，蚂蚁爬行的速度为2cm/s，它想吃到点B处的食物，那么它至少需要爬行 s．
11．如图，一根树在离地面9米处断裂，树的顶部落在离底部12米处．树折断之前有 米．
12．如图，一个三级台阶，它的每一级的长宽和高分别为20、3、2，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是 ．
13．如图，有一四边形空地ABCD，AB⊥AD，AB＝3，AD＝4，BC＝12，CD＝13，则四边形ABCD的面积为 ．
14．一种盛饮料的圆柱形杯，测得内部底面半径为2.5cm，高为12cm，吸管放进杯里（如图），杯口外面至少要露出4.6cm，为节省材料，管长acm的取值范围是 ．
三．解答题
15．一棵高12m的大树被折断，折断处A距地面的距离AC＝4.5m（点B为大树顶端着地处）．在大树倒下的方向停着一辆小轿车，小轿车距大树底部C的距离CD为6.5m，点D在CB的延长线上，求大树顶端着地处B到小轿车的距离BD．
16．如图是某设计师打造的一款项目的示意图，其BC段和垂直于地面的AB段均由不锈钢管材打造，两段总长度为26m，矩形CDEF是一木质平台的侧面示意图，测得CD＝1m，AD＝15m，求出AB段的长度．
17．一架梯子长25米，斜靠在一面墙上，梯子底端离墙7米，
（1）这个梯子的顶端距地面有多高？
（2）如果梯子的顶端下滑了4米到A′，那么梯子的底端在水平方向滑动了几米？
18．数学综合实验课上，同学们在测量学校旗杆的高度时发现：将旗杆顶端升旗用的绳子垂到地面还多2米；当把绳子的下端拉开8米后，下端刚好接触地面，如图，根据以上数据，同学们准确求出了旗杆的高度，你知道他们是如何计算出来的吗？
19．某中学八（1）班小明在综合实践课上剪了一个四边形ABCD，如图，连接AC，经测量AB＝12，BC＝9，CD＝8，AD＝17，∠B＝90°．求证：△ACD是直角三角形．
20．如图，把一块直角三角形（△ABC，∠ACB＝90°）土地划出一个三角形（△ADC）后，测得CD＝3米，AD＝4米，BC＝12米，AB＝13米．
（1）求证：∠ADC＝90°；
（2）求图中阴影部分土地的面积．
21．图1是超市购物车，图2为超市购物车侧面示意图，测得∠ACB＝90°，支架AC＝4.8dm，CB＝3.6dm．
（1）两轮中心AB之间的距离为 dm；
（2）若OF的长度为dm，支点F到底部DO的距离为5dm，试求∠FOD的度数．
22．如图，在一条东西走向河流的一侧有一村庄C，河边原有两个取水点A、B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，该村庄为方便村民取水，决定在河边新建一个取水点H（A、B、H在同一直线上），并新建一条路CH，测得CB＝千米，CH＝3千米，HB＝2千米．
（1）CH是不是从村庄C到河边的最近路？请通过计算加以说明；
（2）求新路CH比原路CA短多少千米？
参考答案
一．选择题
1．解：Rt△ACD中，AC＝AB＝4cm，CD＝3cm；
根据勾股定理，得：AD＝5cm；
∴AD+BD﹣AB＝2AD﹣AB＝10﹣8＝2cm；
故橡皮筋被拉长了2cm．
故选：A．
2．解：由勾股定理得，AB＝10（m），
∴少走的路长为AC+BC﹣AB＝6+8﹣10＝4（m），
故选：D．
3．解：∵侧面对角线BC2＝32+42＝52，
∴CB＝5（cm），
∵AC＝12cm，
∴AB＝13（cm），
∴空木箱能放的最大长度为13cm，
故选：C．
4．解：设旗杆高度为xm，过点C作CB⊥AD于B，
则AC＝AD＝xm，AB＝（x﹣2）m，BC＝8m，
在Rt△ABC中，AB2+BC2＝AC2，即（x﹣2）2+82＝x2，
解得：x＝17，
即旗杆的高度为17米．
故选：D．
5．解：如图，设折断处离地面的高度为x尺，则AB＝10﹣x，BC＝6，
在Rt△ABC中，AC2+BC2＝AB2，即x2+62＝（10﹣x）2．
故选：D．
6．解：如图，设大树高为AB＝10m，
小树高为CD＝4m，
过C点作CE⊥AB于E，则EBDC是矩形，
连接AC，
∴EB＝4m，EC＝8m，AE＝AB﹣EB＝10﹣4＝6m，
在Rt△AEC中，AC＝10m，
故选：B．
7．解：在Rt△ABC中，AB＝2.5米，BC＝1.5米，故AC＝2米，
在Rt△ECD中，AB＝DE＝2.5米，CD＝（1.5+0.5）米，故EC＝1.5米，
故AE＝AC﹣CE＝2﹣1.5＝0.5米．
故选：A．
8．解：延长AB、DC相交于F，则BFC构成直角三角形，
运用勾股定理得：
BC2＝（15﹣3）2+（20﹣4）2＝122+162＝400，
所以BC＝20．
则剪去的直角三角形的斜边长为20cm．
故选：D．
9．解：由勾股定理得：
楼梯的水平宽度＝12，
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和，
地毯的长度至少是12+5＝17米．
故选：B．
二．填空题（共5小题）
10．解：如图所示：
∵底面圆周长为24cm，
∴AB＝12cm，
∵AP＝＝5cm，
∴PB＝13（cm），
∵蚂蚁爬行的速度为2cm/s，
∴它至少需要s．
答：它至少需要s
故答案为：．
11．解：因为AB＝9米，AC＝12米，
根据勾股定理得BC＝15米，
于是折断前树的高度是15+9＝24米．
故答案为：24．
12．解：如图所示，
∵三级台阶平面展开图为长方形，长为20，宽为（2+3）×3，
∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长．
设蚂蚁沿台阶面爬行到B点最短路程为x，
由勾股定理得：x2＝202+[（2+3）×3]2＝252，
解得：x＝25．
故答案为25．
13．解：如图，连接BD，
∵在Rt△ABD中，AB⊥AD，AB＝3，AD＝4，
根据勾股定理得，BD＝5，
在△BCD中，BC＝12，CD＝13，BD＝5，
∴BC2+BD2＝122+52＝132＝CD2，
∴△BCD为直角三角形，
∴S四边形ABCD＝S△ABD+S△BCD
＝AB•AD+BC•BD
＝×3×4+×12×5
＝36．
故答案为：36．
14．解：吸管放进杯里垂直于底面时最短为12+4.6＝16.6；
最长时与底面直径和高正好组成直角三角形，底面直径为2×2.5＝5．
杯里面管长为＝13，总长为13+4.6＝17.6
故管长acm的取值范围是16.6≤a≤17.6．
三．解答题
15．解：在Rt△ABC中，由勾股定理得，
BC＝6（m），
∴BD＝CD﹣BC＝0.5（m），
∴大树顶端着地处B到小轿车的距离BD为0.5米．
16．解：延长FC交AB于点G，
则CG⊥AB，AG＝CD＝1米，GC＝AD＝15米，
设BG＝x米，则BC＝（26﹣1﹣x）米，
在Rt△BGC中，
∵BG2+CG2＝CB2，
∴x2+152＝（26﹣1﹣x）2，
解得x＝8，
∴BA＝BG+GA＝8+1＝9（米），
答：AB的长度长为9米．
17．解：（1）由题意得：AC＝25米，BC＝7米，
AB＝24（米），
答：这个梯子的顶端距地面有24米；
（2）由题意得：BA′＝20米，
BC′＝15（米），
则：CC′＝15﹣7＝8（米），
答：梯子的底端在水平方向滑动了8米．
18．解：设旗杆高xm，则绳子长为（x+2）m，
∵旗杆垂直于地面，
∴旗杆，绳子与地面构成直角三角形，
由题意列式为x2+82＝（x+2）2，解得x＝15m，
∴旗杆的高度为15米．
19．证明：∵∠B＝90°，AB＝12，BC＝9，
∴AC2＝AB2+BC2＝144+81＝225，
∴AC＝15，
又∵AC2+CD2＝225+64＝289，AD2＝289，
∴AC2+CD2＝AD2，
∴△ACD是直角三角形．
20．（1）证明：∵∠ACB＝90°，BC＝12米，AB＝13米，
∴AC＝5（米），
∵CD＝3米，AD＝4米，
∴AD2+CD2＝AC2＝25，
∴∠ADC＝90°；
（2）解：图中阴影部分土地的面积＝AC×BC﹣AD×CD＝×5×12﹣×4×3＝24（平方米）．
21．解：（1）在Rt△ABC中，由勾股定理得：AB＝6（dm），
故答案为：6；
（2）过点F作FH⊥DO，交DO延长线于H，如图所示：
则FH＝5dm，
在Rt△FHO中，由勾股定理得：OH＝5（dm），
∴OH＝FH，
∴△FHO是等腰直角三角形，
∴∠FOH＝45°，
∴∠FOD＝180°﹣∠FOH＝180°﹣45°＝135°，
∴∠FOD的度数为135°．
22．解：（1）CH是从村庄C到河边的最近路．
理由如下：
∵CB＝千米，CH＝3千米，HB＝2千米，
∴CB2＝CH2+HB2，
∴△BCH为直角三角形，∠BHC＝90°，
∴CH⊥AB，
∴CH为C点到AB的最短路线；
（2）设AC＝xkm，则AB＝xkm，AH＝（x﹣2）km，
在Rt△ACH中，（x﹣2）2+32＝x2，解得x＝，
即AC＝km，
∵AC﹣CH＝﹣3＝0.25（km），
答：新路CH比原路CA少0.25千米．