



初中数学苏科版七年级上册6.4 平行精品同步达标检测题
展开6.4
平行
知识梳理
1平行线、平行公理及推论
(1)平行线的定义
在同一平面内,不相交的两条直线叫做平行线,记作a//b.
(2)平行公理
经过直线外一点,有且只有一条直线与这条直线平行。
(3)平行公理的推论
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.即如果//a,//a,那么b//c
2平行线的判定
(1)判定方法1:两条直线被第三条直线所截,如果同位角相等, 那么这两条直线平行.简单说成:同位角相等,两直线平行.
(2)判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行,
(3)判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行。
例题剖析
【例题1】
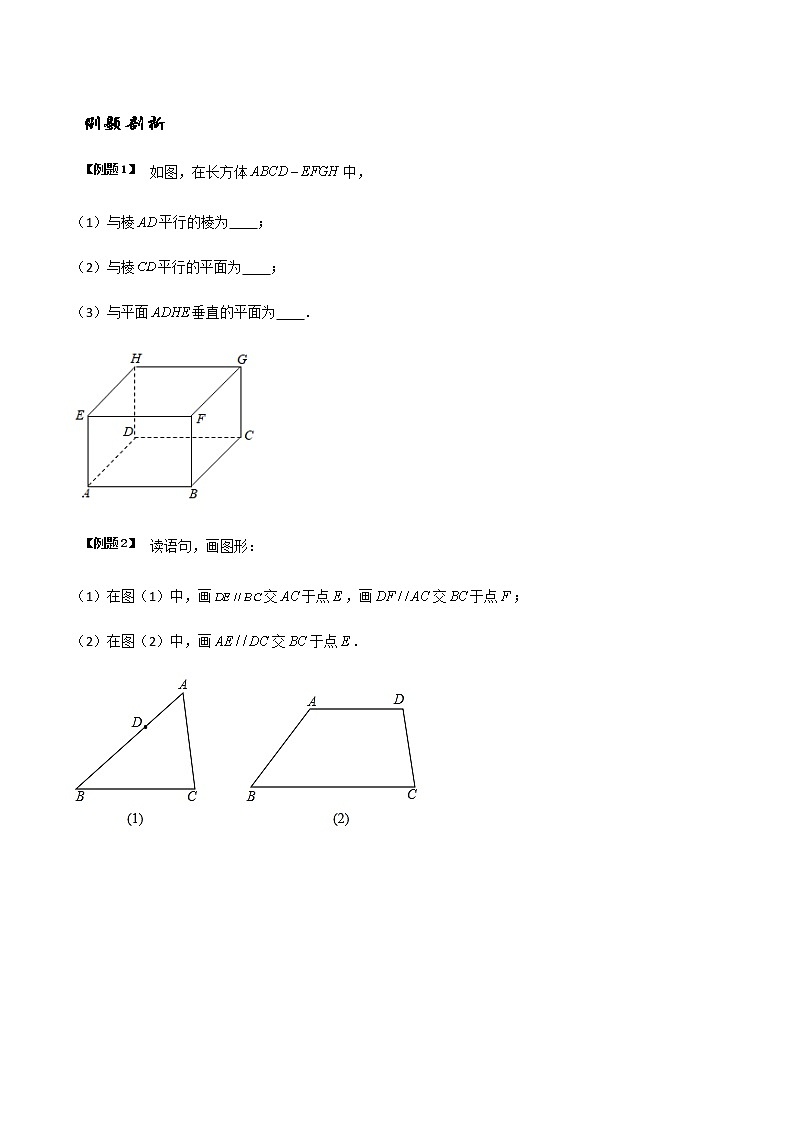
如图,在长方体中,
(1)与棱平行的棱为 ;
(2)与棱平行的平面为 ;
(3)与平面垂直的平面为 .
【答案】(1)棱,,;(2)平面,平面;(3)平面,平面,平面,平面
【分析】
根据平行线的定义,平行的平面的定义,平面与平面垂直的定义等知识解答即可.
【详解】
解:(1)与棱平行的棱为棱,,.
(2)与棱平行的平面为平面,平面.
(3)与平面垂直的平面为平面,平面,平面,平面.
【点睛】
本题考查认识立体图形,平行线的定义,直线与平面平行的定义,平面与平面垂直的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【例题2】
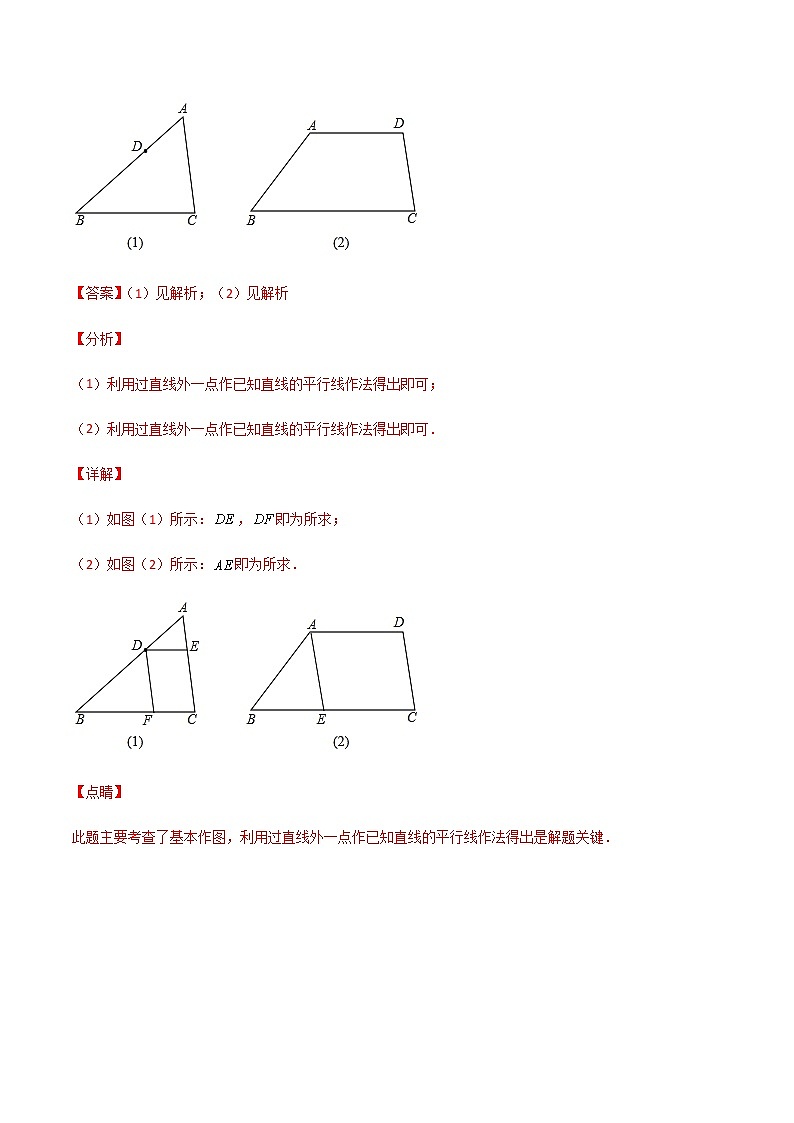
读语句,画图形:
(1)在图(1)中,画交于点,画交于点;
(2)在图(2)中,画交于点.
【答案】(1)见解析;(2)见解析
【分析】
(1)利用过直线外一点作已知直线的平行线作法得出即可;
(2)利用过直线外一点作已知直线的平行线作法得出即可.
【详解】
(1)如图(1)所示:,即为所求;
(2)如图(2)所示:即为所求.
【点睛】
此题主要考查了基本作图,利用过直线外一点作已知直线的平行线作法得出是解题关键.
好题速递
基础巩固
1.已知直线,,互相平行,直线与的距离是,直线与的距离是,那么直线与的距离是( )
A.或B.C.D.
【答案】A
【分析】
分与在同侧和与在两侧两种情况,根据直线与的距离是,直线与的距离是分别求出与的距离即可得答案.
【详解】
①当与在同侧时,
∵直线,,互相平行,直线与的距离是,直线与的距离是,
∴与的距离为5-2=3cm,
②当与在两侧时,
∵直线,,互相平行,直线与的距离是,直线与的距离是,
∴与的距离为5+2=7cm,
综上所述:与的距离是3cm或7cm,
故选:A.
【点睛】
本题考查平行线之间的距离求法,从平行线上任意一点到另一条直线作垂线,垂线段的长度叫做两条平行线之间的距离;灵活运用分类讨论的思想是解题关键.
2.一副三角板按如图方式摆放,点A在EF边上,点D在BC边上,若EFBC,则∠AOD的度数为( )
A.75°B.90°C.105°D.120°
【答案】A
【分析】
由于,且两平行线间有拐点,所以过点O作已知直线的平行线,根据两直线平行,同位角相等,得出部分角的度数,从而得出的度数.
【详解】
解:过点O作EF的平行线PQ,
∵,
∴,
∴,,
∵,
∴.
故选:A.
【点睛】
本题主要考查了平行线的性质,当平行线间有拐点时,过拐点作已知直线的平行线是解题关键.
3.如图,在平面内作已知直线的平行线,可作平行线的条数有( )
A.0条B.1条C.2条D.无数条
【答案】D
【分析】
根据平行线的定义,可直接得结论.
【详解】
解:在同一平面内,与已知直线平行的直线有无数条,
所以作已知直线m的平行线,可作无数条.
故选:D.
【点睛】
本题考查了平行线的定义.掌握平行线的定义是解决本题的关键.
4.已知直线a,b,c是同一平面内的三条不同直线,下面四个结论:
①若则;②若则;③若则;④若且与相交,则与相交,其中,结论正确的是( )
A.①②B.③④C.①②③D.②③④
【答案】A
【分析】
根据平行公理及其推论:在同一平面内,垂直于同一条直线的两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行进行分析即可求解.
【详解】
①根据“同一平面内,如果两条直线都与第三条直线平行,那么这两条直线也互相平行”判定:若则;故说法正确;
②若则,故说法正确;
③根据“在同一平面内,垂直于同一条直线的两直线平行”判定:若则;说法错误;
④若且与相交,则与不一定相交,故说法错误
故正确的有:①②
故选:A
【点睛】
本题主要考查平行公理及其推论,解题的关键是熟练掌握同一平面内两直线的位置关系.
5.下列说法中:
①若两条直线相交所形成的四个角中有三个角相等,则这两条直线互相垂直;
②若,则是线段的中点;
③在同一平面内,不相交的两条线段必平行;
④两点确定一条直线.
其中说法正确的个数( )
A.1B.2C.3D.4
【答案】B
【分析】
根据平行线的定义、垂线的定义、相交线的定义、两点确定一条直线,对各个小题分析判断即可得解.
【详解】
解:①若两条直线相交所形成的四个角中有三个角相等,则这两条直线互相垂直,该说法正确;
②若点C在线段AB上,且,则是线段的中点,原说法错误;
③在同一平面内,不相交的两条直线必平行,原说法错误;
④两点确定一条直线,此说法正确.
故选B.
【点睛】
本题考查了平行线的定义、垂线的定义、相交线的定义、两点确定一条直线,是基础题,熟练掌握概念是解题的关键
6.按语句画图:点在直线上,也在直线上,但不在直线上,直线,,两两相交正确的是( )
A.
B.
C.
D.
【答案】A
【分析】
根据相交线的概念、点与直线的位置关系进行判断即可.
【详解】
解:A.符合条件,
B.不符合点P不在直线c上;
C.不符合点P在直线a上;
D.不符合直线a、b、c两两相交;
故选:A.
【点睛】
本题考查的是相交线、点与直线的位置关系,正确理解题意、认识图形是解题的关键.
7.下列说法正确的是( )
A.没交点的两直线一定平行B.两直线平行一定没交点
C.没交点的线段一定平行D.相交的两直线可能平行
【答案】B
【分析】
根据两直线的位置关系逐一进行判定即可
【详解】
解:A、应为在同一平面内,没有交点的两条直线一定平行,故本选项不符合题意;
B、两直线平行一定没交点,故本选项符合题意;
C、没交点的线段不一定平行,故本选项不符合题意;
D、相交的两直线不可能平行,故本选项不符合题意;
故选:B
【点睛】
本题考查了两直线的位置关系,是基础题,熟记性质与概念是解题的关键.
8.下列说法正确的是( )
A.具有公共顶点的两个角是对顶角
B.两点之间的距离就是线段
C.两点之间,线段最短
D.不相交的两条直线叫做平行线
【答案】C
【分析】
根据对顶角的定义,线段的定义及性质,平行线的定义进行判断
【详解】
解:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,故A选项不符合题意;
两点之间的距离就是线段的长度,故B选项不符合题意;
两点之间,线段最短,故C选项符合题意;
在同一平面内,不相交的两条直线叫做平行线,故D选项不符合题意
故选:C
【点睛】
此题考查对顶角、线段定义及性质已经平行线的概念,正确理解概念是解题关键.
9.在同一平面内,两条直线的位置关系可能是( )
A.相交或垂直B.垂直或平行
C.平行或相交D.相交或垂直或平行
【答案】C
【分析】
根据两条直线有一个交点的直线是相交线,没有交点的直线是平行线,可得答案.
【详解】
在同一平面内,两条直线有一个交点,两条直线相交;在同一平面内,两条直线没有交点,两条直线平行,故C正确;
故选:C.
【点睛】
本题主要考查了同一平面内,两条直线的位置关系,注意垂直是相交的一种特殊情况,不能单独作为一类.
10.在同一平面内,两条直线的位置关系可能是( )
A.相交或平行B.相交或垂直C.平行或垂直D.不能确定
【答案】A
【分析】
根据同一平面内,两条直线的位置关系即可得到结论.
【详解】
解:在同一平面内,两条直线只有两种位置关系:相交或平行,
故选:A.
【点睛】
本题考查平面内两条直线的位置关系,注意垂直是相交的特殊情况,包括在相交里.
11.已知内部有一点,过点画的平行线,这样的直线( )
A.有且只有一条B.有两条C.有三条D.有无数条
【答案】A
【分析】
根据过直线外一点有且仅有一条直线与已知直线平行进行解答即可.
【详解】
根据过直线外一点有且仅有一条直线与已知直线平行,
故选A.
【点睛】
本题主要考查平行线的定义,正确理解平行线的定义是解题的关键.
12.如图,的同位角是( )
A.B.C.D.
【答案】A
【分析】
利用同位角定义可得答案.
【详解】
∠1和∠4是同位角,
∠2和∠5是同位角,
∠3和∠4是同旁内角,
故选:A.
【点睛】
本题主要考查了同位角,关键是掌握同位角的边构成“F“形.
能力提升
1.如图,直线被所截,下列说法,正确的有( )
①与是同旁内角;
②与是内错角;
③与是同位角;
④与是内错角.
A.①③④B.③④C.①②④D.①②③④
【答案】D
【分析】
根据同位角、内错角、同旁内角的定义可直接得到答案.
【详解】
解:①与是同旁内角,说法正确;
②与是内错角,说法正确;
③与是同位角,说法正确;
④与是内错角说法正确,
故选:D.
【点睛】
此题主要考查了三线八角,在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F” 形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
2.如图所示,直线被直线所截,与是( )
A.同位角B.内错角C.同旁内角D.邻补角
【答案】A
【详解】
试题分析:根据两直线被第三条直线所截,所出现的同位角,同旁内角,内错角的特点(三线八角)可直接判断为同位角.
故选A
考点:三线八角
3.如图,直线a,b被直线c所截,则下列说法中错误的是( )
A.∠1与∠2是邻补角B.∠1与∠3是对顶角
C.∠2与∠4是同位角D.∠3与∠4是内错角
【答案】D
【详解】
解:∠3与∠4是同旁内角.
故选:D
4.下列图形中,和不是同位角的是( )
A.B.C.D.
【答案】C
【分析】
在截线的同侧,并且在被截线的同一方的两个角是同位角.
【详解】
解:选项A、B、D中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;
选项C中,∠1与∠2的两条边都不在同一条直线上,不是同位角.
故选:C.
【点睛】
本题考查了同位角的应用,注意:两条直线被第三条直线所截,如果有两个角在第三条直线的同旁,并且在两条直线的同侧,那么这两个角叫同位角.三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.
5.如图,下列四个角中,与∠1构成一对同位角的是( )
A.∠2B.∠3C.∠4D.∠5
【答案】B
【分析】
两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【详解】
解:由图可得,与∠1构成同位角的是∠3,
故选:B.
【点睛】
本题主要考查了同位角的概念,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
6.如图所示的四个图形中,∠1和∠2是同位角的是( )
A.②③B.①②③C.①②④D.①④
【答案】C
【分析】
根据同位角的定义逐一判断即得答案.
【详解】
解:图①中的∠1与∠2是同位角,图②中的∠1与∠2是同位角,图③中的∠1与∠2不是同位角,图④中的∠1与∠2是同位角,
所以在如图所示的四个图形中,图①②④中的∠1和∠2是同位角.
故选:C.
【点睛】
本题考查了同位角的定义,属于基础概念题型,熟知概念是关键.
7.在同一平面内,两条直线的位置关系是( )
A.平行和垂直B.平行和相交C.垂直和相交D.平行、垂直和相交
【答案】B
【分析】
在同一平面内,两条直线的位置关系只有两种情况,平行或相交.
【详解】
解:在同一个平面内,两条直线只有两种位置关系,即平行或相交,
故选:B.
【点睛】
本题主要考查了同一平面内,两条直线的位置关系,注意垂直是相交的一种特殊情况,不能单独作为一类.
8.下列四幅图中,∠1和∠2是同位角的是( )
A.⑴⑵B.⑶⑷C.⑴⑵⑶D.⑵⑶⑷
【答案】A
【分析】
互为同位角的两个角,都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.
【详解】
根据同位角的定义,图(1)、(2)中,∠1和∠2是同位角;
图(3)中∠1、∠2的两边都不在同一条直线上,不是同位角;
图(4)中∠1、∠2不在被截线同侧,不是同位角.
故选A
【点睛】
本题考查了同位角的定义,在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.
9.如图,直线、被直线所截,则与是( )
A.内错角B.同位角C.同旁内角D.对顶角
【答案】B
【分析】
根据三线八角的概念,以及同位角的定义作答即可.
【详解】
解:如图所示,∠1和∠2两个角都在两被截直线b和c同侧,并且在第三条直线a(截线)的同旁,故∠1和∠2是直线b、c被a所截而成的同位角.
故选:B.
【点睛】
本题考查了同位角、内错角、同旁内角的定义.在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.两条直线被第三条直线所截所形成的八个角中,有四对同位角,两对内错角,两对同旁内角.
10.若a⊥b,c⊥d,则a与c的关系是( )
A.平行B.垂直C.相交D.以上都不对
【答案】D
【分析】
分情况讨论:①当b∥d时;②当b和d相交但不垂直时;③当b和d垂直时;即可得出a与c的关系.
【详解】
当b∥d时a∥c;
当b和d相交但不垂直时,a与c相交;
当b和d垂直时,a与c垂直;
a和c可能平行,也可能相交,还可能垂直.
故选:D.
【点睛】
本题考查了直线的位置关系,掌握平行、垂直、相交的性质是解题的关键.
中考真题
1.在同一平面内,两条不重合的直线的位置关系是 ( )
A. 平行 B. 相交 C. 相交或平行 D. 垂直
【答案】 C
【详解】解: 在同一平面内,两条不重合的直线的位置关系是相交或平行.
故答案为:C.
【分析】根据在同一平面内,两条不重合的直线的位置关系是相交或平行,即可求解.
2.已知点M(9,-5)、N(-3,-5),则直线MN与x轴、y轴的位置关系分别为( )
A. 相交、相交 B. 平行、平行 C. 垂直相交、平行 D. 平行、垂直相交
【答案】 D
【详解】解:∵点M和点N的纵坐标相等
∴直线MN与x轴平行,与y轴垂直相交
故答案为:D.
【分析】根据题意,由点M以及点N的坐标确定直线MN,确定其与x轴以及y
轴的关系即可。
3.三条直线相交,交点最多有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】 C
【详解】解:三条直线相交时,位置关系如图所示:
判断可知:最多有3个交点,
故答案为:C.
【分析】分别画出三条直线相交的情况,然后找出交点个数即可.
4.在同一平面内,两条直线可能的位置关系式( )
A. 平行 B. 相交 C. 相交或平行 D. 垂直
【答案】 C
【详解】解:在同一个平面内,两条直线只有两种位置关系,即平行或相交.
故答案为:C.
【分析】根据在同一个平面内两条直线的位置关系进行分析即可.
5.在同一平面内,不重合的两条直线的位置关系是( )
A. 平行 B. 相交 C. 相交或垂直 D. 相交或平行
【答案】 D
【详解】解:在同一平面内,不重合的两条直线的位置关系是相交或平行,相交包含垂直.
故答案为:D.
【分析】根据在同一平面内,两条直线的位置关系判断.
6.观察图形,下列说法正确的个数是( )
(1)直线BA和直线AB是同一条直线;(2)AB+BD>AD;(3)射线AC和射线AD是同一条射线;(4)三条直线两两相交时,一定有三个交点
A. 1个 B. 2个 C. 3个 D. 4个
【答案】 C
【详解】(1)直线BA和直线AB是同一条直线;正确,
( 2)AB+BD>AD;正确
( 3)射线AC和射线AD是同一条射线;正确,
( 4)三条直线两两相交时,一定有三个交点,还可能有一个,故不正确.
共3个说法正确.
故答案为:C.
【分析】根据直线、射线、线段的表示法、三角形三边关系以及两条直线相交只有一个交点,逐项进行判断,找出正确的说法,即可求解.
7.三条直线a、b、C,若a∥c,b∥c,则a与b的位置关系是( )
A. a⊥b B. a∥b C. a⊥b或a∥b D. 无法确定
【答案】 B
【详解】解:∵ a∥c,b∥c ,
∴a∥b,
故答案为:B.
【分析】平行线具有传导性,即两条直线同时和第三条直线平行,则这两条直线平行。
8.在同一个平面内,不重合的两条直线的位置关系是( )
A. 平行或垂直 B. 相交或垂直 C. 平行或相交 D. 不能确定
【答案】 C
【详解】在同一平面内,两条不重合的直线的位置关系是平行或相交.
故答案为:C.
【分析】根据在同一平面内两条不重合的直线的位置关系得出即可.
9.在同一平面内,不重合的两条直线的位置关系有( )
A. 平行或相交 B. 平行或垂直 C. 平行、垂直或相交 D. 相交或垂直
【答案】 A
【详解】解:同一平面内,不重合的两条直线平行或相交。
故答案为:A.
【分析】根据同一平面内的两条直线的关系进行判断即可。
10.在同一平面内,不重合的两条直线的位置关系有( )
A. 平行和相交 B. 平行和垂直 C. 平行、垂直和相交 D. 垂直和相交
【答案】 A
【详解】解:平面内的直线有平行和相交两种位置关系.
故答案为:A.
【分析】同一平面内,直线的位置关系通常有两种:平行或相交.垂直是相交的特殊情况.
初中数学苏科版七年级上册6.4 平行同步训练题: 这是一份初中数学苏科版七年级上册6.4 平行同步训练题,共5页。试卷主要包含了单选题,填空题等内容,欢迎下载使用。
数学七年级上册6.4 平行精品练习题: 这是一份数学七年级上册6.4 平行精品练习题,文件包含同步讲义苏科版数学七年级上册64平行原卷版docx、同步讲义苏科版数学七年级上册64平行解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
初中数学苏科版七年级上册6.4 平行精品课后练习题: 这是一份初中数学苏科版七年级上册6.4 平行精品课后练习题,文件包含64平行-七年级数学上册同步精品讲义苏科版解析版docx、64平行-七年级数学上册同步精品讲义苏科版原卷版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。













