2021-2022学年北京市西城区七年级（下）期末数学试卷（Word解析版）

2021-2022学年北京市西城区七年级（下）期末数学试卷

一、选择题（本大题共8小题，共16分。在每小题列出的选项中，选出符合题目的一项）

1. 在平面直角坐标系中，点所在象限为(    )

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

2. 若，则下列各式中正确的是(    )

A.  B.  C.  D.

3. 如图，，点在上，过点作的垂线交于点若，则的大小为(    )

A.  B.  C.  D.

4. 下列命题不正确的是(    )

A. 经过直线外一点，有且只有一条直线与这条直线平行
B. 在同一平面内，过一点有且只有一条直线与已知直线垂直
C. 连接直线外一点与直线上各点的所有线段中，垂线段最短
D. 在同一平面内，垂直于同一条直线的两条直线互相垂直

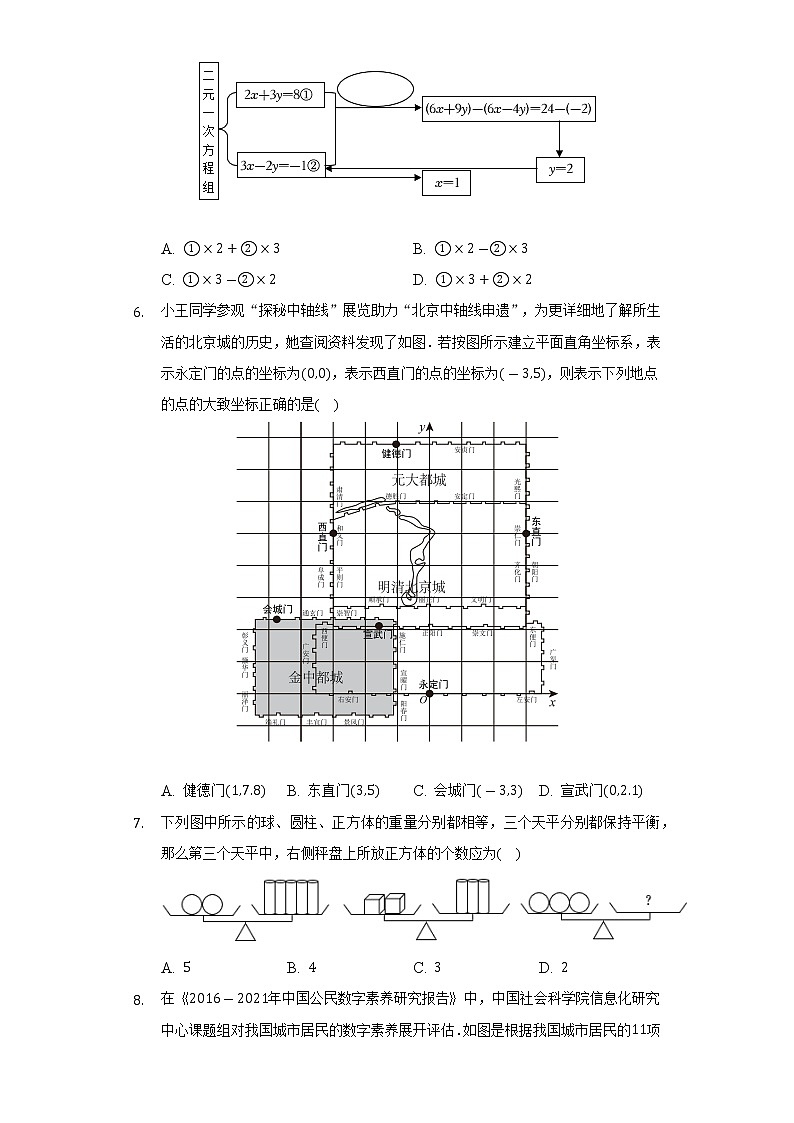
5. 解方程组的思路可用如图的框图表示，圈中应填写的对方程所做的变形为(    )

A.  B.
C.  D.

6. 小王同学参观“探秘中轴线”展览助力“北京中轴线申遗”，为更详细地了解所生活的北京城的历史，她查阅资料发现了如图．若按图所示建立平面直角坐标系，表示永定门的点的坐标为，表示西直门的点的坐标为，则表示下列地点的点的大致坐标正确的是(    )

A. 健德门 B. 东直门 C. 会城门 D. 宣武门

7. 下列图中所示的球、圆柱、正方体的重量分别都相等，三个天平分别都保持平衡，那么第三个天平中，右侧秤盘上所放正方体的个数应为(    )

A.  B.  C.  D.

8. 在年中国公民数字素养研究报告中，中国社会科学院信息化研究中心课题组对我国城市居民的数字素养展开评估．如图是根据我国城市居民的项数字素养平均值制作的统计图．根据统计图提供的信息，下面关于我国城市居民数字素养指标的判断不正确的是(    )

A. 信息真实性判别表现最好
B. 数字内容创建能力表现最弱
C. 专业领域数字化应用能力的表现要好于数字化协作的表现
D. 平均值高于的指标有智能手机应用、信息真实性判别、数字安全意识

二、填空题（本大题共8小题，共16分）

9. 若是方程的解，则的值为______．
10. 如图，直线，指定位置的三条射线，，满足，有以下两个结论：与一定共线；其中正确的结论是______只填写序号．

11. 在实数中，无理数是______．
12. 在等式中，内的数等于______．
13. 在平面直角坐标系中，到轴的距离等于______．
14. 将命题“同角的补角相等”改写成“如果那么”形式为______．
15. 操作任务：将初始图九宫格中剪开的格图片进行平移，拼出目标图九九消寒图．
    操作规则：为了有效地记录、检验和交流平移过程，小明和同伴约定用“有序数对”描述平移方式并填写操作记录图，约定如下：将初始图中的初始位置图片进行平移，横向移动标记在前，纵向移动标记在后，将向右或向上平移格记为正号可省略，反之记为以此类推，不移动记为如“前”字在对应位置标记为．
    操作过程：
    操作记录图中“”位置应填______；
    判断：操作记录图中，是否有应标记的位置，请在答题卡上选择“有”或“无”，如果选择“有”，请同时将相应网格涂黑．

16. 与最接近的整数是______，简述判断过程：______．

三、解答题（本大题共10小题，共78分。解答应写出文字说明，证明过程或演算步骤）

17. 计算：；
    已知，求的值．
18. 解不等式组在数轴上表示出它的解集，并求它的整数解．
19. 如图，在中，点在边上，点，分别在，边上，，，的延长线上一点满足．
    求证：；
    请将下面的证明过程补充完整：
    证明：，，
    ，
    ______理由：______
    ，
    ____________理由：______
    理由：______
    图中与相等的角是______．

20. 随着我国物流行业市场的成熟发展和技术成熟度的显著提升，物流无人机的市场价格下降很快，物流无人机得到了广泛的应用，已知架甲型物流无人机与架乙型物流无人机总价为万元，架甲型物流无人机与架乙型物流无人机总价为万元．甲型和乙型物流无人机每架各多少万元？
21. 在平面直角坐标系中，，将线段先向左平移个单位，再向下平移个单位得到线段其中点的对应点为点，点的对应点为点，线段恰好过点线段上的点平移后的对应点为点．
    补全图形，直接写出点和点的坐标；
    画出四边形并求它的面积．

22. 故宫博物院为鼓励游客参与“故宫零废弃”项目做好垃圾分类，在“数字故宫”小程序中推出了一项体验活动，将故宫改造升级后的垃圾桶编号并精心布局，在每个垃圾桶点位共个设置一道与院内场景相关的篆体古字题目，游客点击相应点位的垃圾桶编号解答题目，以形会意，看字识“物”，并在感受中国传统文化的同时，了解垃圾分类知识．
    
    王老师在全年级随机邀请了名学生在线参与答题，小明所在小组收集、整理同学们看字识“物”和辨别垃圾的答题成绩并制作统计图表成绩设为百分制下面是这名学生成绩的频数分布表、频数分布直方图数据分成组：，，，，以及部分数据信息．
    成绩频数分布表

成绩频数分布直方图

这一组的成绩是：
，，，，，，，，，，，，，，．
根据以上信息，回答下列问题：
请补全成绩频数分布表和成绩频数分布直方图；
直接写出这名学生中，成绩不低于分的人数；
若小明所在年级的名学生参与此项活动，估计这名学生中有多少人成绩不低于分．

23. 小明设计了如下一个小程序，用户运行此程序时，先在第一象限内任取一个点，程序就会在该点的右上方按逆时针方向画一个长方形包含可能出现正方形的情况，且水平边的长等于这一点的横坐标，竖直边的长等于这一点的纵坐标，称此长方形为“程序长方形”．
    
    图所示的五个长方形，记为图形Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，其中程序长方形是______，程序长方形最初所取点的坐标为______．
    如图，小明在第一象限画了个整点即横、纵坐标都为整数的点，，，，，程序相应地可画出个长方形．
    实验探究：
    在射线上任取一点不同于点，则该点所对应的程序长方形的水平边与竖直边的长度之比等于______．
    在直线位于第一象限的部分上任意取几个点，写出这些点所对应的程序长方形的一条共同特征；
    记点Ⅰ所对应的程序长方形的面积为若要画一个整点，使它对应的程序长方形的面积小于且周长尽可能大，直接写出点的坐标．
     

24. 已知，点在射线上，点在外部，，以为顶点，为一边，大小为的角的另一边交射线于点．
    如图，当点与点位于所在直线异侧时，的平分线与射线的交点为点补全图形并直接写出直线与直线的位置关系；
    当点与点位于所在直线同侧时，射线与射线交于点，点在线段的延长线上．
    如图，若平分，求证：平分；
    当时，直接写出的度数并画出符合题意的图形．
     

25. 对于实数，可用表示不超过的最大整数．例如：，．
    ______，______；
    若实数满足，求满足条件的的值．
26. 在平面直角坐标系中，对于点，，若这个点的横坐标的最大值为，纵坐标的最大值为，将记为，，，，称为这个点的“平面特征值”如对于，，，．
    如图，，，正方形的边在轴上，边与轴正半轴的交点为点．
    ，，______；
    已知，过点作直线轴，直线与直线交于点，直线与直线交于点记，，，．
    当时，______；
    用含的式子表示，判断当点在轴上运动时，是否存在最大值或最小值，如果存在，写出的值以及相应点的坐标．

答案和解析

1.【答案】 

【解析】解：点所在象限为第四象限．
故选：．
根据各象限内点的坐标特征解答．
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限；第二象限；第三象限；第四象限．
 

2.【答案】 

【解析】解：、在不等式的两边同时加上，不等号方向不变，即，故本选项不符合题意．
B、在不等式的两边同时减去，不等号方向不变，即，故本选项不符合题意．
C、在不等式的两边同时乘，不等号方向改变，即，故本选项符合题意．
D、在不等式的两边同时除以，不等号方向不变，即，故本选项不符合题意．
故选：．
根据不等式的性质进行判断．
本题主要考查了不等式，熟练掌握不等式的性质是解答本题的关键．运用不等式的性质应注意的问题：在不等式的两边都乘以或除以同一个负数时，一定要改变不等号的方向；当不等式的两边要乘以或除以含有字母的数时，一定要对字母是否大于进行分类讨论．
 

3.【答案】 

【解析】解：过点作的垂线交于点，
，
，，
，
．
故选：．
由垂直可得，再由平行线的性质得，从而可求的度数．
本题主要考查平行线的性质，解答的关键是熟记平行线的性质并灵活运用．
 

4.【答案】 

【解析】解：、经过直线外一点，有且只有一条直线与这条直线平行，正确，不符合题意；
B、在同一平面内，过一点有且只有一条直线与已知直线垂直，正确，不符合题意；
C、连接直线外一点与直线上各点的所有线段中，垂线段最短，正确，不符合题意；
D、在同一平面内，垂直于同一条直线的两条直线互相平行，故错误，符合题意．
故选：．
利用平行线的性质与判定方法、垂线的性质等知识分别判断后即可确定正确的选项．
本题考查了命题与定理的知识，解题的关键是了解平行线的性质与判定方法、垂线的性质等知识，难度不大．
 

5.【答案】 

【解析】解：，
，得，
，得，
，得，
即变形的思路是，
故选：．
消去未知数，变形思路是，再得出选项即可．
本题考查了解二元一次方程组，能把二元一次方程组转化成一元一次方程是解此题的关键．
 

6.【答案】 

【解析】解：如图，
表示永定门的点的坐标为，表示西直门的点的坐标为，
图中小正方形的边长为．
A、健德门，不符合题意；
B、东直门，符合题意；
C、会城门，不符合题意；
D、宣武门，不符合题意．
故选：．
由已知条件推知：图中小正方形的边长为，据此进行一一分析判断．
本题主要考查坐标确定位置，解题的关键是确定原点位置及各点的横纵坐标．
 

7.【答案】 

【解析】解：设一个球的质量为，一个圆柱体的质量为，一个正方体的质量为，由题意得，
，，
即，，
，，
即，
右侧秤盘上所放正方体的个数应为，
故选：．
设一个球的质量为，一个圆柱体的质量为，一个正方体的质量为，根据天平平衡的条件可得，，再根据等式的性质得到即可．
本题考查认识立体图形、等式的性质，掌握等式的性质是解决问题的前提．
 

8.【答案】 

【解析】解：根据统计图提供的信息得，
A.信息真实性判别表现最好，正确，不符合题意；
B.数字内容创建能力表现最弱，正确，不符合题意；
C.专业领域数字化应用能力的平均值为，数字化协作的平均值为，
数字化协作的表现要好于专业领域数字化应用能力的表现，判断不正确，符合题意；
D.平均值高于的指标有智能手机应用、信息真实性判别、数字安全意识，正确，不符合题意；
故选：．
根据条形统计图中的数据即可求解．
此题考查了条形统计图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．
 

9.【答案】 

【解析】解：把代入方程得：，
，
故答案为：．
把代入方程，得到关于的一元一次方程，解方程即可求出的值．
本题考查了二元一次方程的解，把方程的解代入方程，得到关于的一元一次方程是解题的关键．
 

10.【答案】 

【解析】解：如图，延长射线交直线于点，直线于点，

，
，
，，
，
，故结论错误；
，，
，故结论正确．
故答案为：．
根据平行线的性质对各结论进行分析即可．
本题主要考查平行线的性质，解答的关键是熟记平行线的性质并灵活运用．
 

11.【答案】 

【解析】解：，，是整数，属于有理数；
是分数，属于有理数；
无理数是．
故答案为：．
根据无理数的定义无理数是指无限不循环小数逐个判断即可．
本题考查了无理数的定义和算术平方根，能熟记无理数的定义是解此题的关键，无理数包括三方面的数：开方开不尽的根式，含有的，一些有规律的数，如两个之间依次多一个等．
 

12.【答案】或 

【解析】解：设内的数为，则等式即为，
两边开平方得，或，
解得，或．
即内的数等于或．
故答案为：或．
设内的数为，利用直接开平方法解方程，求出即可．
本题考查了解一元二次方程直接开平方法，形如或的一元二次方程可采用直接开平方的方法解一元二次方程．
 

13.【答案】 

【解析】解：在平面直角坐标系中，到轴的距离等于，
故答案为：．
根据点到轴的距离等于横坐标的绝对值解答．
本题考查了点的坐标，熟记点到轴的距离等于横坐标的绝对值是解题的关键．
 

14.【答案】如果两个角是同一个角的补角，那么这两个角相等 

【解析】

【分析】
本题考查了命题的叙述，正确分清命题的条件和结论是把命题写成“如果那么”的形式的关键．
“同角的补角相等”的条件是：两个角是同一个角的补角，结论是：这两个角相等．据此即可写成所要求的形式．
【解答】
解：“同角的补角相等”的条件是：两个角是同一个角的补角，结论是：这两个角相等．
则将命题“同角的补角相等”改写成“如果那么”形式为：如果两个角是同一个角的补角，那么这两个角相等．
故答案是如果两个角是同一个角的补角，那么这两个角相等．  

15.【答案】 

【解析】解：“”是初始图中的柳向上平移格得到，
“”位置应填，
故答案为：；

有，如图所示．垂的位置表示．

根据有序数对的定义判断即可；
寻找没有移动的文字即可．
本题考查作图利用平移设计图案，解题的关键是理解题意，灵活运用所学知识解决问题．
 

16.【答案】  到的距离小于到的距离 

【解析】解：，
，
即，
而，
更接近的整数是，
故答案为：，理由：到的距离小于到的距离．
估算无理数的大小，再根据到这两个整数的距离的大小即可．
本题考查估算无理数的大小，掌握算术平方根的定义是正确判断的前提，理解“到的距离小于到的距离，说明更接近整数”是正确判断的关键．
 

17.【答案】解：

．
，
，
方法：解得，
．
方法：得：，
． 

【解析】首先计算开平方、开立方和绝对值，然后从左向右依次计算，求出算式的值即可．
首先根据题意，可得：，方法：应用加减消元法，求出方程组的解，再把求出的、的值代入计算即可；方法：计算即可．
此题主要考查了实数的运算，注意运算顺序，偶次方、绝对值的非负性质的应用，以及解二元一次方程组的方法，注意代入消元法和加减消元法的应用．
 

18.【答案】解：，
解不等式得：；
解不等式得：，
原不等式组的解集为：，
该不等式组的解集在数轴上表示如图所示：

该不等式组的整数解为：，，． 

【解析】按照解一元一次不等式组的步骤，进行计算即可解答．
本题考查了解一元一次不等式组，在数轴上表示不等式的解集，熟练掌握解一元一次不等式组是解题的关键．
 

19.【答案】  等角的余角相等      等量代换  内错角相等，两直线平行  和 

【解析】证明：，，，
理由：等角的余角相等，
，
理由：等量代换，
理由：内错角相等，两直线平行，
故答案为：；等角的余角相等；；；等量代换；内错角相等，两直线平行；
解：，
，，
，
，
，
即，
图中与相等的角是和，
故答案为：和．
根据等角的余角相等得出，进而推出，即可判定；
根据平行线的性质及角的和差求解即可．
此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．
 

20.【答案】解：设甲型物流无人机每架万元，乙型物流无人机每架万元，
根据题意得，，
解得：，
答：甲型物流无人机每架万元，乙型物流无人机每架万元． 

【解析】设甲型物流无人机每架万元，乙型物流无人机每架万元，根据“架甲型物流无人机与架乙型物流无人机总价为万元，架甲型物流无人机与架乙型物流无人机总价为万元”即可列出二元一次方程组．
本题主要考查了二元一次方程组的应用，根据总价找出等量关系是解决问题的关键．
 

21.【答案】解：线段即为所求，，；

如图，四边形即为所求，
，
． 

【解析】根据平移的性质，即可画出图形，并得出点的坐标；
先利用割补法求出四边形的面积，再根据点为的中点，得出面积关系．
本题主要考查了作图平移变换，图形的面积等知识，熟练掌握割补法求四边形的面积是解题的关键．
 

22.【答案】解：由题意知，的人数为，的人数为，的人数为，的人数为，
补全表格和图形如下：

成绩不低于分的人数为人；
人，
答：估计这名学生中有人成绩不低于分． 

【解析】结合表格和直方图可得答案；
根据表格中的数据即可得出答案；
用总人数乘以样本中成绩不低于分的人数所占比例即可．
本题考查频数分布表、频数分布直方图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．
 

23.【答案】Ⅲ和  与  ： 

【解析】解：由图可知，将五个长方形左下角坐标开始依次逆时针代入题设条件得，满足条件的程序长方形是Ⅲ和．
左下角的点即为最初所取点，即分别为与，
故答案为：Ⅲ和； 与．
由图可知，
设直线的解析式为，
将点代入解析式得：．
射线的解析式为：
由题设可知，设所取点坐标为，
则，，
水平边长度为：，竖直边长度为：
水平边与竖直边的长度之比：．
故答案为：：．
这些点所对应的程序长方形的一条共同特征是水平边与竖直边的长度之和为，
由图可知，，，
设直线的解析式为，
将，代入，
，解得，
直线的解析式为：．
设所取点坐标为，
则 ， ，，
水平边长度为，竖直边长度为．
这些点所对应的程序长方形的一条共同特征是水平边与竖直边的长度之和为：．
点坐标或，理由如下：
由程序长方形四个点的坐标可知：它的面积等于，
，则，
小于的正整数为，，，，，
若要画一个整点，使它对应的程序长方形的面积小于且周长尽可能大，
点坐标或．
根据“程序长方形”的定义可直接判断．
由题意可知，射线的解析式为：设所取点坐标为，则，，水平边长度为：，竖直边长度为：
由此可得出水平边与竖直边的长度的比；
由点，的坐标可知，直线的解析式为：设所取点坐标为，则 ， ，，由此可得，水平边长度为，竖直边长度为由此可得出结论；
由程序长方形四个点的坐标可知：它的面积等于，由，则，因为小于的正整数为，，，，，所以若要画一个整点，使它对应的程序长方形的面积小于且周长尽可能大，由图形可知，点坐标或．
本题是平面直角坐标系背景下的新定义类问题，考查待定系数法求函数解析式，四边形的面积，平面直角坐标系中线段长的求法等知识，关键是理解“程序长方形”的定义．
 

24.【答案】解：补全图形如图所示，此时，理由如下：

平分，且，
，
，
，
，
，
．
证明：
，
，，．
，，
，．
平分，
．
．
．
．
平分．
解：如图，

，
，
，
，
，
，解得． 

【解析】补全图形如图所示，此时，有平分，且，可得，由，可得，所以．
因为，所以，，因为平分，所以，所以所以由此可得结论．
由，可知，，所以，所以，解得之即可得出结论．
本题考查的是三角形的内角和定理、平行线的性质和角平分线的性质与判定，解答此题的关键是熟知角平分线的定义和性质．
 

25.【答案】   

【解析】解：由题意可得，
，，
故答案为：，；
设，为整数部分，为小数部分，
和均为整数，，
为整数，
只能为，，，，，
当时，，
，

，
当时，，
解得，
为非负整数，
或，
或，
或；
当时，，
解得，
为整数，
，
，
；
当时，，
，
，
当时，
，
解得，
，
与矛盾，无解；
当时，
，
解得，
，
与矛盾，无解；
由上可得：满足条件的的值为或或．
根据题意，可以写出相应的结果；
根据题意和题目中的式子，利用分类讨论的方法可以求得的值．
本题考查解一元一次不等式、新定义，解答本题的关键是明确题意，利用分类讨论的数学思想解答．
 

26.【答案】   

【解析】解：，，
，，
，，，
故答案为：；
如图，正方形的中心为，

当时，，
，，
，，，，
故答案为：；
当时，，，
，
当时，，
当时，，，
，
综上：，
当时，随的增大而增大，当时，随的增大而减小，
时，存在最小值为，此时．
根据“平面特征值”的定义直接可得答案；
当时，得出，，则，，，；
分，，三种情形，分别表示出、的坐标，再利用“平面特征值”的定义可得与的函数解析式，再根据函数的增减性可得最小值．
本题是四边形综合题，主要考查了正方形的性质，一次函数的性质，理解“平面特征值”的定义，表示出点、的坐标是解题的关键．