
2021-2022学年北京市燕山区七年级(下)期末数学试卷-(Word解析版)
展开一、选择题(本题共8小题,共24分)
5的相反数是( )
A. 5B. -5C. -15D. 15
北京2022年冬奥会的开幕式上,各个国家和地区代表团入场所持的引导牌是中国结和雪花融合的造型,如图是中国体育代表团的引导牌.下面四个图案中,可以通过平移图得到的是( )
A. B.
C. D.
在数轴上表示不等式x-3≥0的解集,正确的是( )
A. B.
C. D.
如图是天安门周围的景点分布示意图.在图中,分别以正东,正北方向为x轴,y轴的正方向建立平面直角坐标系.如果表示景山的点的坐标为(0,4),表示王府井的点的坐标为(3,1),则表示人民大会堂的点的坐标为( )
A. (3,2)
B. (-1,2)
C. (-1,-1)
D. (-1,-2)
下列调查中,适合采用抽样调查方式的是( )
A. 调查本校七年级(1)班学生每天完成数学作业所用的时间
B. 调查全市中学生对电影《长津湖之水门桥》的喜爱程度
C. 调查“神舟十四号”运载火箭发射前零部件质量状况
D. 调查某封控区全体人员核酸检测情况
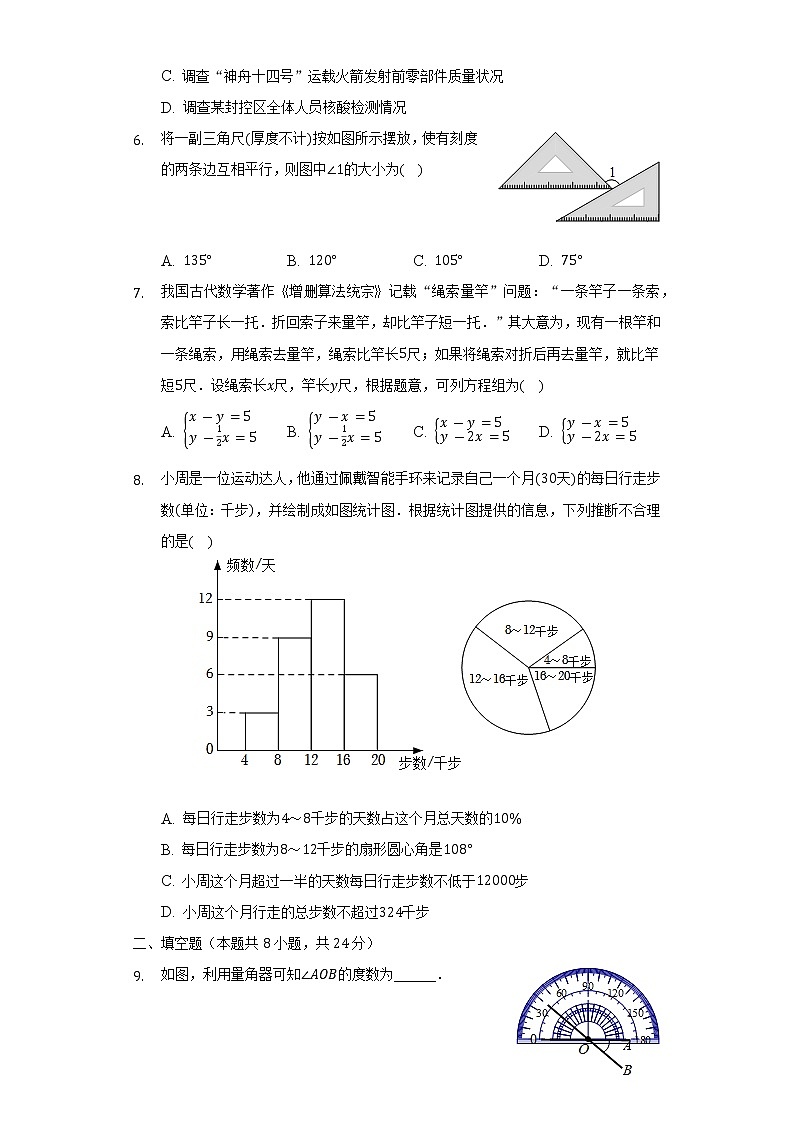
将一副三角尺(厚度不计)按如图所示摆放,使有刻度的两条边互相平行,则图中∠1的大小为( )
A. 135°B. 120°C. 105°D. 75°
我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子来量竿,却比竿子短一托.”其大意为,现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,根据题意,可列方程组为( )
A. x-y=5y-12x=5B. y-x=5y-12x=5C. x-y=5y-2x=5D. y-x=5y-2x=5
小周是一位运动达人,他通过佩戴智能手环来记录自己一个月(30天)的每日行走步数(单位:千步),并绘制成如图统计图.根据统计图提供的信息,下列推断不合理的是( )
A. 每日行走步数为4~8千步的天数占这个月总天数的10%
B. 每日行走步数为8~12千步的扇形圆心角是108°
C. 小周这个月超过一半的天数每日行走步数不低于12000步
D. 小周这个月行走的总步数不超过324千步
二、填空题(本题共8小题,共24分)
如图,利用量角器可知∠AOB的度数为______.
x的一半与4的差是负数,用不等式表示为______.
若a
如图,要使CD//BE,需要添加的一个条件为:______.
已知x=-1y=2是方程为3x+my=5的解,则m的值为______.
在平面直角坐标系中,点P(a,1)位于第二象限且到y轴的距离为2,则a的值是______.
已知m是整数,且π
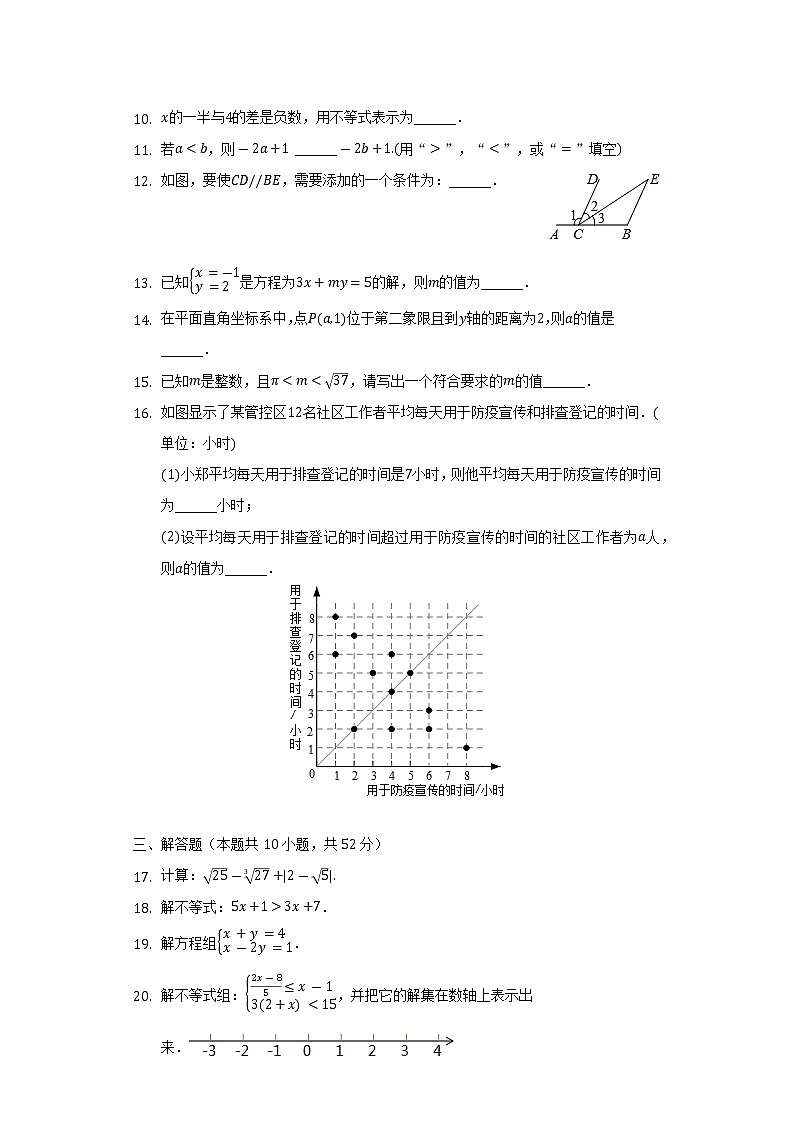
(1)小郑平均每天用于排查登记的时间是7小时,则他平均每天用于防疫宣传的时间为______小时;
(2)设平均每天用于排查登记的时间超过用于防疫宣传的时间的社区工作者为a人,则a的值为______.
三、解答题(本题共10小题,共52分)
计算:25-327+|2-5|.
解不等式:5x+1>3x+7.
解方程组x+y=4x-2y=1.
解不等式组:2x-85≤x-13(2+x)<15,并把它的解集在数轴上表示出来.
如图,点P为∠AOB内一点,根据下列语句画图并回答问题:
(1)画图:①过点P画OB边的垂线,垂足为点M;
②过点P画OB边的平行线,交OA于点N.
(2)若∠O=120°,则∠ANP=______°,依据是______;
(3)连接OP,则线段OP与PM的大小关系是______,依据是______.
如图,已知AB//CD,CF为∠ACD的平分线,∠A=110°,∠EFC=35°.
求证:EF//CD.
请将下面的证明过程补充完整.
证明:∵AB//CD,(已知)
∴∠______+∠ACD=180°,
∵∠A=110°,(已知)
∴∠ACD=______°.(等量代换)
∵CF为∠ACD的平分线,(已知)
∴∠FCD=12∠=35°.(角平分线定义)
∵∠EFC=35°,(已知)
∴∠FCD=∠EFC,(等量代换)
∴EF//CD.
某中学为了解家长对课后延时服务的满意度,随机抽取50名学生家长进行问卷调查,获得了每位家长对课后延时服务的评分数据(记为x),并对数据进行整理、描述和分析,制作了课后延时服务家长评分数据的频数分布表如下:
(1)表中a=______,b=______.
(2)下面是A,B,C三位同学分别绘制的课后延时服务家长评分数据的频数分布直方图,
其中只有一位同学的作图正确,则作图正确的同学是______;
(3)已知该校共有600名学生家长参加了此次调查评分,请你估计其中大约有多少名家长的评分不低于80分.
“冰墩墩”和“雪容融”作为第24届北京冬奥会和冬残奥会的吉祥物深受大家喜爱.某公司为奖励在趣味运动会上取得好成绩的员工,计划购买“冰墩墩”和“雪容融”玩偶共20件作为奖品.已知“冰墩墩”玩偶的零售单价是198元,“雪容融”玩偶的零售单价是100元.
(1)如果购买“冰墩墩”和“雪容融”玩偶共花费了2784元,求“冰墩墩”和“雪容融”玩偶各购买了多少件?
(2)如果购买“雪容融”玩偶的件数不超过“冰墩墩”玩偶件数的2倍,请为该公司设计一种最省钱的购买方案,并求出此时的总费用.
如图,点A,B分别为∠MON的边OM,ON上的定点,点C为射线ON上的动点(不与点O,B重合).连接AC,过点C作CD⊥AC,过点B作BE//OA,交直线CD于点F.
(1)如图1,若点C在线段OB的延长线上,
①依题意补全图1;
②用等式表示∠OAC与∠BFC的数量关系,并说明理由;
(2)如图2,若点C在线段OB上,直接用等式表示出∠OAC与∠BFC的数量关系.
对于平面直角坐标系xOy中的任意一点P(x,y),给出如下定义:记a=x-y,b=x+y,将点M(a,b)与点N(b,a)称为点P的一对伴随点.例如,点M(5,1)与点N(1,5)为点P(3,-2)的一对伴随点.
(1)点A(4,1)的一对伴随点坐标为______;
(2)将点C(m+1,3m-1)(m>0)向右平移m个单位长度,得到点C',若点C'的一对伴随点重合,求点C的坐标;
(3)已知点E(n,-2),F(n+1,-2),点D为线段EF上的动点,点G,H为点D的一对伴随点.当点D在线段EF上运动时,线段GH与y轴总有公共点,请直接写出n的取值范围.
答案和解析
1.【答案】B
【解析】解:5的相反数是-5.
故选:B.
根据只有符号不同的两个数互为相反数,可得答案.
本题考查了实数的性质,在一个数的前面加上负号就是这个数的相反数.
2.【答案】A
【解析】解:能通过平移得到的是A选项图案.
故选:A.
根据平移只改变图形的位置不改变图形的形状和大小、方向解答.
本题考查了利用平移设计图案,熟记平移变换只改变图形的位置不改变图形的形状并准确识图是解题的关键.
3.【答案】B
【解析】解:依题意得:x≥3,所以不等式的解集在数轴上的表示为B.
本题要求在数轴上表示不等式的解集,可先对不等式进行化简,得出x的取值.数轴上的箭头方向表示数字的递增,若不等式的取值含有等号,则在该点的表示是实心的,若取不到,则在该点的表示是空心的.
本题考查的是数轴的表示方法.学生容易把B、C两个答案混淆.要注意本题x可取到3,因此在数轴上表示3的点是实心的.
4.【答案】D
【解析】解:如图所示:人民大会堂的点的坐标为是:(-1,-2).
故选:D.
直接利用已知点坐标进而确定原点位置进而得出答案.
此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
5.【答案】B
【解析】解:A.调查本校七年级(1)班学生每天完成数学作业所用的时间,适合全面调查,故选项不符合题意;
B.调查全市中学生对电影《长津湖之水门桥》的喜爱程度,适合抽样调查,故选项符合题意;
C.调查“神舟十四号”运载火箭发射前零部件质量状况,适合全面调查,故选项不符合题意;
D.调查某封控区全体人员核酸检测情况,适合全面调查,故选项不符合题意.
故选:B.
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答即可.
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
6.【答案】C
【解析】解:如图:
∵AB//CD,
∴∠ABC=∠BCD=30°,
∵∠ABE=45°,
∴∠1=180°-∠ABE-∠ABC=105°,
故选:C.
根据平行线的性质可得∠ABC=30°,然后利用平角定义进行计算即可解答.
本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
7.【答案】A
【解析】解:根据题意得:x-y=5y-12x=5.
故选:A.
由绳索比竿长5尺,可得x=y+5①,由将绳索对半折后再去量竿,就比竿短5尺,可得12x=y-5 ②.
本题主要考查函数的实际应用,考查转化思想,属于基础题.
8.【答案】D
【解析】解:A.330×100%=10%,即每日行走步数为4~8千步的天数占这个月总天数的10%,故本选项不合题意;
B.每日行走步数为8~12千步的扇形圆心角是360°×930=108°,故本选项不合题意;
C.小周这个月每日行走步数不低于12000步的天数有12+6=18(天),故本选项不合题意;
D.小周这个月行走的总步数约为:3×6+9×10+12×14+6×18=384(千步),故本选项符合题意;
故选:D.
A选项,用每日行走步数为4~8千步的天数除以总天数即可判断;B选项,用360°乘每日行走步数为8~12千步的天数所占比例即可判断;C选项,根据条形统计图的数据判断即可;D选项,把各种数据相加即可判断.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
9.【答案】40°
【解析】解:根据对顶角相等得:∠AOB=40°,
故答案为:40°.
根据对顶角相等即可得出答案.
本题考查了对顶角相等,掌握对顶角相等是解题的关键.
10.【答案】12x-4<0
【解析】解:根据题意得:12x-4<0.
故答案为:12x-4<0.
“x的一半”即12x,“与4的差”可表示为12x-4,根据负数即“<0”可得不等式.
此题主要考查了由实际问题抽象出一元一次不等式,读懂题意,抓住关键词语,弄清运算的先后顺序和不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.
11.【答案】>
【解析】解:∵a
∴-2a+1>-2b+1.
故答案为:>.
根据不等式的基本性质判断即可.
本题考查了不等式的性质,掌握①不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;②不等式的两边同时乘(或除以)同一个正数,不等号的方向不变;③不等式的两边同时乘(或除以)同一个负数,不等号的方向改变是解题的关键.
12.【答案】∠2=∠E或∠1=∠B或∠B+∠BCD=180°
【解析】解:当∠2=∠E时,由内错角相等,两直线平行得CD//BE;
当∠1=∠B时,由同位角相等,两直线平行得CD//BE;
当∠B+∠BCD=180°时,由同旁内角互补,两直线平行得CD//BE.
故需要添加的条件为:∠2=∠E或∠1=∠B或∠B+∠BCD=180°.
故答案为:∠2=∠E或∠1=∠B或∠B+∠BCD=180°.
利用平行线的判定条件进行分析即可.
本题主要考查平行线的判定,解答的关键是熟记平行线的判定的条件并灵活运用.
13.【答案】4
【解析】解:把x=-1y=2代入方程得:-3+2m=5,
解得:m=4,
故答案为:4.
把x与y的值代入方程计算即可求出m的值.
此题考查了二元一次方程的解,解答的关键是明确方程的解即为能使方程左右两边相等的未知数的值.
14.【答案】-2
【解析】解:∵点P在第二象限,且到y轴的距离为2,
∴点P的横坐标是-2,
即a的值为-2.
故答案为:-2.
根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值是解题的关键.
15.【答案】6(答案不唯一)
【解析】解:∵π<36<37,
∴π<6<37,
∴m的值是6;
故答案为:6(答案不唯一).
先估算出37的大小,再按要求写出一个符合条件的m的值即可.
本题考查无理数大小的估算,解题的关键是能能正确估算37的近似值.
16.【答案】2 5
【解析】解:(1)如图
图中点C表示平均每天用于排查登记的时间是7小时,
则该同学平均每天用于防疫宣传的时间为2小时,
故答案为:2;
(2)设平均每天用于排查登记的时间超过用于防疫宣传的时间的社区工作者为a人,
则图中点A,点B,点C,点D,点E符合题意,
∴a=5,
故答案为:5.
(1)理解题意的基础上,观察统计图,找到符合题意的关键点,从而读取数据;
(2)理解题意的基础上,观察统计图,找到符合题意的关键点,从而读取数据进行计算.
本题考查统计的应用,理解题意,准确识图,确定符合题意的关键点是解题关键.
17.【答案】解:原式=5-3+5-2
=5.
【解析】直接利用二次根式的性质以及立方根的性质、绝对值的性质分别化简,进而合并得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
18.【答案】解:移项得:5x-3x>7-1,
合并得:2x>6,
解得:x>3.
【解析】不等式移项,合并,把x系数化为1,即可求出解集.
此题考查了解一元一次不等式,熟练掌握不等式的解法是解本题的关键.
19.【答案】解:x+y=4 ①x-2y=1 ②
①-②得:(x+y)-(x-2y)=4-1
y+2y=33y=3y=1
把y=1代入①得:x+1=4,
x=3
∴原方程组的解为x=3y=1
【解析】用加减消元法解方程组即得到答案.
本题考查了二元一次方程组的解法,解题关键是认真观察未知数系数并适当选用消元方法解方程.
20.【答案】解:解不等式2x-85≤x-1,得:x≥-1,
解不等式3(2+x)<15,得:x<3,
所以,原不等式组的解集是-1≤x<3,
在数轴上表示为:
.
【解析】先求出不等式组的解集,在数轴上表示不等式组的解集.
本题考查了解一元一次不等式组,在数轴上表示不等式组的解集,不等式组的整数解等知识点,能根据不等式的解集求出不等式组的解集是解此题的关键.
21.【答案】120 两直线平行,同位角相等 OP>PM 垂线段最短
【解析】解:(1)如图,
(2)∵PN//OB,
∴∠ANP=∠AOB=120°.
故答案为:120;两直线平行,同位角相等;
(3)∵PM⊥OB于M,
∴OP>PM.
故答案为:OP>PM;垂线段最短.
(1)根据几何语言画出对应的几何图形;
(2)根据平行线的性质求解;
(3)根据垂线段最短判断线段OP与PM的大小关系.
本题考查了作图—复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行线的性质和垂线段最短.
22.【答案】A 70
【解析】证明:∵AB//CD,(已知)
∴∠A+∠ACD=180°,
∵∠A=110°,(已知)
∴∠ACD=70°,(等量代换)
∵CF为∠ACD的平分线,(已知)
∴∠FCD=12∠=35°,(角平分线定义)
∵∠EFC=35°,(已知)
∴∠FCD=∠EFC,(等量代换)
∴EF//CD.
故答案为:A,70.
先根据平行线的性质求出∠ACD的度数,根据角平分线的定义可得∠FCD的度数,然后得∠FCD=∠EFC=35°,进而根据内错角相等,两直线平行证得结论.
此题考查了平行线的判定与性质,解题的关键是:熟记同位角相等⇔两直线平行,内错角相等⇔两直线平行,同旁内角互补⇔两直线平行.
23.【答案】18 30% B
【解析】解:(1)b=1550×100%=30%,
∴a=150×36%=18,
故答案为:18,30%;
(2)由题意得:作图正确的同学是B,
故答案为:B;
(3)600×(36%+20%)=336(名),
答:估计其中大约有336名家长的评分不低于80分.
(1)根据表中的数据以及抽取总数即可得a,b的值;
(2)根据表中的数据即可判断;
(3)用总人数乘以样本中成绩在80分以上(含80分)人数所占比例即可.
本题考查统计表、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
24.【答案】解:(1)设“冰墩墩”玩偶购买了x件,“雪容融”玩偶购买了y个,
依题意得:x+y=20198x+100y=2784,
解得:x=8y=12.
答:“冰墩墩”玩偶购买了8件,“雪容融”玩偶购买了12个.
(2)设购买“雪容融”玩偶m件,则购买“冰墩墩”玩偶(20-m)件,
依题意得:m≤2(20-m),
解得:m≤403,
∵m为整数,
∴m≤13.
又∵“冰墩墩”玩偶的单价高于“雪容融”玩偶的单价,
∴购买“雪容融”玩偶越多,所需总费用越少,
∴当m=13时,20-m=20-13=7,此时所需总费用为100×13+198×7=2686(元).
答:最省钱的购买方案为:购买“雪容融”玩偶13件,“冰墩墩”玩偶7件,此时的总费用为2686元.
【解析】(1)设“冰墩墩”玩偶购买了x件,“雪容融”玩偶购买了y个,利用总价=单价×数量,结合购买20件玩偶所需总费用为2784元,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买“雪容融”玩偶m件,则购买“冰墩墩”玩偶(20-m)件,根据购买“雪容融”玩偶的件数不超过“冰墩墩”玩偶件数的2倍,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,结合m为整数值即可得出m的最大值,结合“冰墩墩”玩偶的单价高于“雪容融”玩偶的单价,即可得出最省钱的购买方案,再利用总价=单价×数量,即可求出此时所需总费用.
本题考查了二元一次方程组的应用、一元一次不等式的应用以及有理数的混合运算,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
25.【答案】解:(1)①补全图形如下:
②∠OAC+∠BFC=90°;理由如下:
设BE交AC于G,
∵CD⊥AC,
∴∠FCG=90°,
∴∠FGC+∠BFC=90°,
∵OA//BE,
∴∠OAC=∠FGC,
∴∠OAC+∠BFC=90°;
(2)∠BFC=90°+∠OAC,理由如下:
延长AC交直线BE于H,如图:
∵BE//OA,
∴∠OAC=∠CHF,
∵CD⊥AC,
∴∠FCH=90°,
∵∠BFC=∠FCH+∠CHF,
∴∠BFC=90°+∠OAC.
【解析】(1)①根据题意补全图形即可;
②设BE交AC于G,由CD⊥AC,可得∠FGC+∠BFC=90°,又OA//BE,有∠OAC=∠FGC,即得∠OAC+∠BFC=90°;
(2)延长AC交直线BE于H,由BE//OA,得∠OAC=∠CHF,又CD⊥AC,知∠FCH=90°,即可得∠BFC=90°+∠OAC.
本题考查本题考查相交线,平行线,解题的关键是画出图形,掌握平行线性质,垂直的定义及三角形内角和定理及推论.
26.【答案】(3,5),(5,3)
【解析】解:由题意得,a=x-y=4-1=3,
b=x+y=4+1=5
∴点A的一对伴随点坐协为:(3,5),(5,3);
(2)由题意得,C'(2m+1,3m-1),
此时,a=2m+1-3m+1=-m+2,
b=2m+l+3m-1=5m,
则C'点的伴随点为(-m+2,5m)和(5m,-m+2),
∴这两个伴随点重合,(即两点的横、纵坐标分别相等),
∴-m+2=5m,解得,m=13,
∴m+1=43,3m-1=0,
∴C点坐标为(43,0);
(3)∵D为线段EF上的动点,
设D点坐标为(t,-2)(n≤t≤n+1),
∴D点的伴随点为:a=t+2,b=t-2,即(t+2,t-2),(t-2,t+2),
∴G(t+2,t-2),H(t-2,t+2),
∵线段GH与y轴总有公共点,t+2>t-2,
∴t+2≥0t-2≤0,解得:-2≤t≤2,
由n≤t≤n+1,
可得,n≥-2n+1≤2,解得,-2≤n≤1,
∴n的取值范围为:-2≤n≤1.
(1)根据“伴随点”的定义求解即可;
(2)根据“伴随点”的定义列方程求解即可;
(3)设出点D的坐标,根据新定义,建立不等式组,即可得出结论.
本题考查了一次函数的性质,新定义,解方程及不等式组,理解和应用新定义是解题的关键.
分组
划记
频数(人)
百分比
0≤x<60
2
4%
60≤x<70
正
5
10%
70≤x<80
正正正
15
b
80≤x<90
正正正
a
36%
90≤x≤100
正正
10
20%
2021-2022学年北京市密云区七年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年北京市密云区七年级(下)期末数学试卷(Word解析版),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年北京市房山区八年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年北京市房山区八年级(下)期末数学试卷(Word解析版),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年北京市燕山区八年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年北京市燕山区八年级(下)期末数学试卷(Word解析版),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












