专题3.3 幂函数-2022-2023学年高一数学阶段性复习精选精练（人教A版2019必修第一册）

专题3.3   幂 函 数

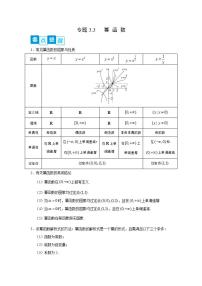
1．常见幂函数的图象与性质

2．有关幂函数的常用结论

（1）幂函数在上都有定义.

（2）幂函数的图象均过定点.

（3）当时，幂函数的图象均过定点，且在上单调递增.

（4）当时，幂函数的图象均过定点，且在上单调递减.

（5）幂函数在第四象限无图象.

3．求幂函数解析式的方法：幂函数的解析式是一个幂的形式，且需满足以下三个条件：

（1）指数为常数；

（2）底数为自变量；

（3）系数为1.

一、单选题

1．下列结论中，正确的是

A．幂函数的图象都经过点(0，0)，(1，1)

B．幂函数的图象可以出现在第四象限

C．当幂指数α取1，3，时，幂函数y＝xα是增函数

D．当α＝－1时，幂函数y＝xα在其整个定义域上是减函数

2．下列函数中，不是幂函数的是

A．y＝2x  B．y＝x－1

C．y＝  D．y＝x2

3．若函数为幂函数，且在单调递减，则实数的值为

A．0  B．或

C．1  D．2

4．已知幂函数的图象经过点(2，4)，则f(-2)＝

A．-9  B．9

C．4  D．-4

5．已知幂函数，则实数等于

A．2  B．1

C．0  D．任意实数

6．已知幂函数的图象过点，则该函数的解析式为

A．  B．

C．  D．

7．若幂函数 (m，n∈N*，m，n互质)的图象如图所示，则

A．m，n是奇数，且<1     B．m是偶数，n是奇数，且>1

C．m是偶数，n是奇数，且<1   D．m是奇数，n是偶数，且>1

8．已知幂函数y=f(x)=xa的图象经过点(2，4)，则f(-3)=

A．-9  B．9

C．3  D．-3

9．已知是奇函数，当时，，则的值是

A．8  B．8

C．4  D．4

10．若为幂函数，且在上单调递减，则的解析式可以是

A．  B．

C．  D．

11．如图表示的时四个幂函数在同一坐标系中第一象限内的图象，则幂函数的图象可能是

A．①  B．②

C．③  D．④

12．函数的定义域为

A．  B．

C．  D．

13．已知幂函数（）在时是增函数，在时是减函数，则n的值是

A．正奇数  B．负奇数

C．正偶数  D．负偶数

14．若幂函数的图象经过点，则在定义域内

A．为增函数  B．为减函数

C．有最小值  D．有最大值

15．如图是幂函数的部分图象，已知取，2，，这四个值，则与曲线，，，相应的依次为

A．2，，， B．，，，2

C．，2，， D．2，，，

16．已知幂函数的图象过点，则

A．  B．2

C．1  D．4

17．已知函数，则下列结论正确的是

A．的定义域为    B．在定义域上为减函数

C．是偶函数      D．是奇函数

18．已知幂函数y＝f(x)经过点(3，)，则f(x)

A．是偶函数，且在(0，＋∞)上是增函数

B．是偶函数，且在(0，＋∞)上是减函数

C．是奇函数，且在(0，＋∞)上是减函数

D．是非奇非偶函数，且在(0，＋∞)上是增函数

19．在同一坐标系内，函数和的图象可能是

A． B．

C． D．

20．幂函数是偶函数，且在（0，+∞）上是减函数，则m的值为

A．﹣6  B．1

C．6  D．1或﹣6

21．已知幂函数f(x)的图象为曲线C，在命题：①f(x)为偶函数；②曲线C不过原点O；③曲线C在第一象限呈上升趋势；④当x≥1时，f(x)≥1中，只有一个假命题，则该命题是（ ）

A．①  B．②

C．③  D．④

22．若幂函数f（x）的图象过点（64，2），则f（x）＜f（x2）的解集为

A．（﹣∞，0） B．（0，1）

C．（1，+∞） D．（0，1）∪（1，+∞）

23．已知幂函数（p，q∈Z且p，q互质）的图象关于y轴对称，如图所示，则

A．p，q均为奇数，且    B．q为偶数，p为奇数，且

C．q为奇数，p为偶数，且   D．q为奇数，p为偶数，且

24．已知函数是幂函数，且在上递减，则实数m=

A．2  B．1

C．4  D．2或1

25．幂函数的图象过点(-2，)，则它的单调递增区间是

A．(0，+∞)  B．[0，+∞)

C．(-∞，+∞)  D．(-∞，0)

26．已知是幂函数，且在上单调递增，则满足的实数的范国为

A．  B．

C．  D．

27．幂函数的图象经过点，则的值为

A．1  B．-1

C．0  D．2

28．已知幂函数，其图象与坐标轴无交点，则实数的值为

A．或  B．

C．或  D．

29．函数 的图象是

A． B．

C． D．

30．若幂函数在上单调递增，则

A．  B．

C．  D．

二、多选题

1．若点在幂函数的图象上，则下列结论可能成立的是

A．  B．

C．  D．

2．下列关于幂函数的性质，描述正确的有

A．当时函数在其定义域上是减函数 B．当时函数图象是一条直线

C．当时函数是偶函数 D．当时函数在其定义域上是增函数

3．下列说法中错误的是

A．幂函数的图象不经过第四象限

B．的图象是一条直线

C．若函数的定义域为，则它的值域为

D．若函数的值域为是，则它的定义域一定是

4．已知幂函数，则下列结论正确的有

A．

B．的定义域是

C．是偶函数

D．不等式的解集是

5．设，则使函数的定义域为且为奇函数的所有的值有

A．  B．

C．  D．

6．下列关于幂函数的性质说法正确的有

A．当时，函数在其定义域上递减

B．当时，函数图象是一条直线

C．当时，函数是偶函数

D．当时，函数的图象与轴交点的横坐标为

7．函数和在同一直角坐标系中图象不可能是图中的

A． B．

C． D．

8．已知幂函数，对任意，且，都满足，若且，则下列结论可能成立的有

A． 且 B． 且

C． 且 D．以上都可能

9．已知幂函数的图象经过，则幂函数具有的性质是

A．在其定义域上为增函数 B．在上单调递减

C．奇函数 D．定义域为

10．已知幂函数，则下列结论正确的有

A． 

B．是偶函数

C．若，则 

D．若，则

三、填空题

1．幂函数经过点，则___________．

2．已知幂函数的图象过点，则___________．

3．如图是幂函数（αi＞0，i＝1，2，3，4，5）在第一象限内的图象，其中α1＝3，α2＝2，α3＝1，，，已知它们具有性质：

①都经过点（0，0）和（1，1）；   ②在第一象限都是增函数．

请你根据图象写出它们在（1，+∞）上的另外一个共同性质：___________．

4．已知幂函数，若函数为奇函数，且在是减函数，则___________．

5．己知幂函数的图象过点，则___________．

6．已知幂函数的图象过点，则=___________．

7．已知α∈．若幂函数f(x)＝xα为奇函数，且在(0，＋∞)上递减，则＝___________．

8．函数是幂函数，且在上是减函数，则实数__________．

9．已知幂函数的图象经过点，则___________．

10．已知幂函数的图象过点，则它的单调递减区间是___________．

11．已知幂函数过定点，且满足，则的范围为________．

12．若幂函数的图象过点，则函数的最大值为___________．

13．关于的不等式的解集为___________．

14．若函数是幂函数，且在上单调递增，则实数___________．

15．已知函数，若对任意，恒成立，则的取值范围是___________．

四、双空题

1．已知幂函数的图象过点，则___________，___________．

2．已知幂函数的图象过点，则___________，由此，请比较下列两个数的大小：___________．

3．若函数为幂函数，则实数的值为___________；当此幂函数在单调递减，则实数的值为___________．

4．函数的定义域为___________，值域为___________．

5．已知幂函数过点（3，3），则k+a=___________；若函数，则g（x）的值域为___________．

五、解答题

1．已知幂函数（）是偶函数，且在上单调递增．

（1）求函数的解析式；

（2）若，求的取值范围；

2．已知幂函数y＝f(x)的图象过点．

（1）求函数f(x)的解析式，利用定义法证明函数的单调性；

（2）求满足f（1＋a）＞f（3－a）的实数a的取值范围．

3．分别写出下列函数的定义域，并指出它们的奇偶性：

（1）；       

（2）；

（3）；       

（4）．

4．已知幂函数是偶函数，且在上单调递增．

（1）求函数的解析式；

（2）若，求的取值范围：

（3）若实数满足，求的最小值．

5．已知幂函数(，)在区间上单调递减．

（1）求的解析式；

（2）当时，恒成立，求的取值范围．